5511-04

CIS 5511. Programming Techniques

Sorting (1)

1. The sorting problem

The sorting problem: input, output, value, order.

Why to study it: practical and conceptual reasons.

Default data structure: array. Default order: non-decreasing. Major operations: element comparisons and assignments.

Common algorithms of comparison sort and their time costs:

Θ(n²): Bubble Sort, Selection Sort, Insertion Sort
Θ(n^1.x): [Shellsort]
Θ(n lg n): Mergesort, [Timsort,] Heapsort, Quicksort

Other considerations:

Whether to demand all inputs at the beginning, and whether to produce all outputs at the same time. E.g., Insertion Sort, Selection Sort
Space cost: "in place" or not. E.g. Merge Sort needs 2n space, while Insertion Sort needs constant amount.

2. Heaps

A tree is a data structure in which every node, except one called "root", has exactly one predecessor (parent) and any number of (zero or one or several) successors (children) that are usually distinguished by order (i.e., 1st, 2nd, 3rd, etc.).

A binary tree is a tree data structure in which each node has at most a left successor (child) and a right (successor) child.

A (binary) heap is a complete binary tree (which is filled by level, and at each level from left to right) that is "sorted vertically" in the sense that the values on every path are sorted. In a max-heap, the value of a parent is never smaller than that of its children; in a min-heap, the value of a parent is never larger than that of its children.

A heap is usually stored in an array, where the order of elements is the same as how the tree is filled. The root of the tree is A[1], and given the index i of a node, the index of its parent is Parent(i) = floor(i/2) (except for the root), the index of its left child is Left(i) = 2i, and the index of its right child is Right(i) = 2i+1.

For example, the following max-heap (a) is stored in the array (b).

The height of a node in a heap is the number of edges on the longest path from the node to a leaf. The height of a heap is the height of its root. If a heap has n nodes, its height is Θ(lg n).

3. Heapify

The algorithm Max-Heapify(A, i) fixes a heap in A by moving A[i] to the right place, under the assumption that its children Left(i) and Right(i) are already (roots of) heaps.

Example: Max-Heapify(A, 2), where heap-size[A] = 10.

At most two comparisons are needed between one node and its children. The children's subtrees each have size at most 2n/3, and the worst case occurs when the last row is half full.

Therefore, the running time of the algorithm can be described as T(n) ≤ T(2n/3) + Θ(1). The master theorem solves this recurrence with result T(n) = O(lg n), which is the same as the height of the heap.

4. Heap building

We can use the Heapify algorithm to convert an array into a heap. The basic idea is to skip the leaves, and to fix the upper-level nodes one by one in the reverse order until the root.

Example:

Since Max-Heapify is O(lg n), and it is called less than n times in Build-Max-Heap, the latter is surely O(n lg n). However, this upper bound is not tight, and it can be proved that Build-Max-Heap is O(n), as there are more elements near the leaves than those near the root.

5. Heapsort

It is easy to sort a heap: just repeatedly exchange the root and the last element, then fix the heap after each step. Heapsort is an "in place" algorithm.

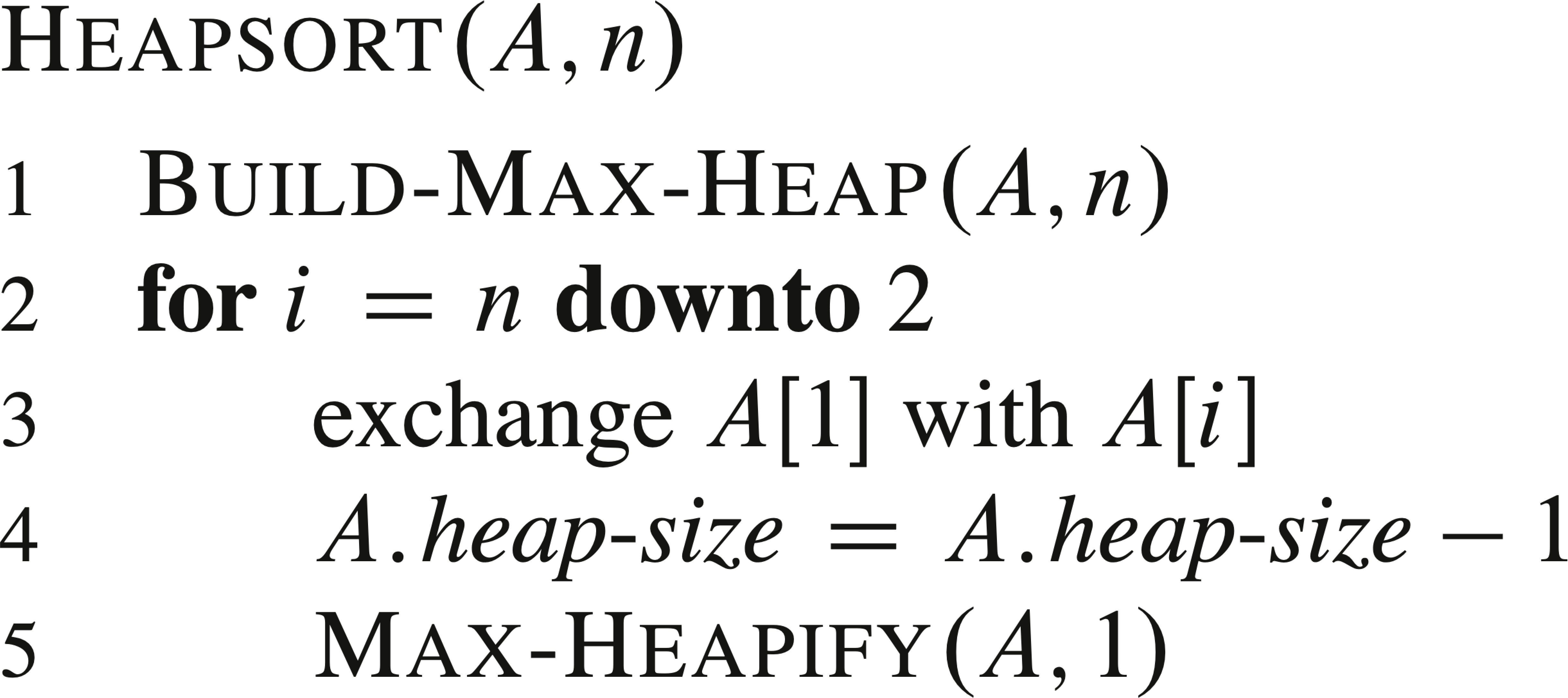
Example:

Heapsort is O(n lg n), because Build-Max-Heap takes time O(n), and each of the n − 1 calls to Max-Heapify takes O(lg n) time.

6. Priority queues

A priority queue is an abstract data structure in which each item has a priority value attached, and there is an operation, usually the same as deletion, that removes the item with the highest priority.

To use a heap to implement a priority queue, item with the highest priority is the root. After the root is removed from the heap, the last item is moved into root, then the heap is fixed in a top-down way.

On the other hand, the "insert" operation adds a new item at the end of the heap, then fix the heap in a bottom-up way, by calling the "increase-key" algorithm that increase the key of x to k.

Example of "increase-key":

All the above operations cost O(lg n) time. A heap can be built by repeating Max-Heap-Insert, but it will be less efficient than the Build-Max-Heap algorithm when all the values are available at the beginning.

If a priority queue is implemented by a sorted array, then insertion takes O(n) time, and deletion takes O(1) time; if it is implemented by a unsorted array, then insertion takes O(1) time, and deletion takes O(n) time.

If the priority of items only takes m (a finite number) possible values, a priority queue can be implemented by an array of queues, where insertion and deletion take only O(1) time.