1. Algorithm and data structure

An algorithm is a procedure consisting of computational steps that transforms an input value into an output value, where

• the steps are directly executable,
• the procedure is predetermined and has a finite-length description,
• the process will terminate for every valid input with an output.

For example, "sorting" is a problem where the input is a sequence of items of a certain type, with a total order defined between any pair of them, and the output should be a sequence of the same items, arranged according to the order. A sorting algorithm should specify, step by step, how to turn any valid input into the corresponding output in finite time, then stop (halt) there.

An algorithm is correct if for every valid input instance, it halts with the output as specified in the problem. An algorithm is incorrect if there is a valid input instance for which the algorithm produces an incorrect answer or no answer at all (i.e. does not halt).

For a given problem, if there are multiple candidate algorithms, which one should be used? There are several factors to be considered:

• correctness
• time and space efficiency
• conceptual simplicity

When the (input, output, or intermediate) data of a problem contain multiple components, they are usually organized in a data structure, which represents both the data items and the relations among them.

A data structure can be specified either abstractly, in terms of the operations (as computations) that can be carried out on it, or concretely, in terms of the storage organization and the algorithms accomplishing the operations. An abstract data structure often corresponds to multiple concrete ones.

In the design and selection of data structures, the analysis of the algorithms involved is a central topic.

Programming means to code an algorithm in a computer language. A program is language-specific, while an algorithm is language-independent.

2. Time efficiency analysis

For a given program, the actual time it takes to solve a given problem instance depends on

• the algorithm implemented in the program,
• the given problem instance,
• the software and hardware in which the program is executed.

As a starting point, the following instructions are usually assumed to be directly executable and each takes a constant amount of time.

• arithmetic: add, subtract, multiply, divide, remainder, floor, ceiling;
• comparison: equal to, larger than, smaller than;
• data movement: load, store, copy, assign;
• control: conditional and unconditional branch, subroutine call and return.

To measure the time complexity of algorithms, the common practice is to define a size (usually using n) for each instance of the problem (which intuitively measures the relative difficulty of processing the instance), then to represent the running time as a function of this instance size (as T(n) in the following). Finally, the increasing rate of the function, with respect to the increasing of the instance size, is used as the indicator of the efficiency or complexity of the algorithm.

With such a procedure, algorithm analysis becomes a mathematical problem, which is well-defined, and the result has universal validity.

Though it is a powerful technique, we need to keep in mind that many relevant factors have been ignored in this process, and therefore, if for certain reason some of the factors have to be taken into consideration, the traditional algorithm analyzing approach may become improper to use.

3. Conventions about pseudocode

• The looping and the conditional constructs are similar to those in C/Java/Python/Pascal.
• Indentation indicates block structure, without delimiters.
• Assignment sign is equal sign, "=", and multiple assignment is allowed.
• Double equal sign, "==", is for equality.
• The boolean operators and and or are short circuiting.
• Variables are defined within an algorithm and do not require declaration.
• Array elements are represented as A[index], and index usually starts at 1. A[i:j] is a subarray consisting A[i] ... A[j].
• A field in an object is represented as object.field (array length is Array.length in the 3rd edition).
• Parameters are passed to a procedure by value.
• A return statement transfers control back to the calling procedure.
• Double slash ("//") is used for comments.
• Lines are numbered.

4. Example: sort using an incremental approach

Insertion sort works by repeatedly insert an element into the sorted part of the array.

The correctness of the algorithm is proven by checking the loop invariant, which is a proposition about a relation among certain variables, such as

At the start of each iteration of the for loop of line 1-8, the subarray A[1 : i−1] consists of the elements originally in A[1 : i−1] but in sorted order.

• Initialization: It is true prior to the first iteration of the loop.
• Maintenance: If it is true before an iteration of the loop, it remains true before the next iteration.
• Termination: When the loop terminates, the invariant helps showing the correctness of the algorithm.

For sorting, it is natural to use the number of keys to be sorted as input size, and it is assumed that a constant amount of time is required to execute each line of the pseudocode (except comments).

Now let us mark the cost and the number of execution times of each line:

In line 5-7, t_i is the number of executions of Line 5 for the i value.

The running time of the algorithm is

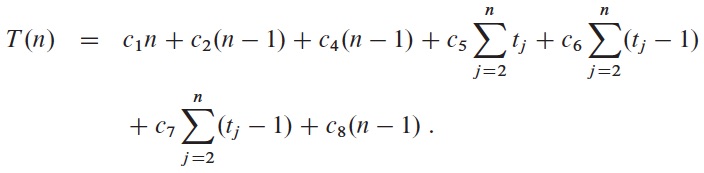
For a given n, T(n) depends on the values of t_j, which changes from instance to instance.

For a given size n, the best case of the algorithm happens when the array is already sorted, so that t_i = 1 for i = 2, 3, ..., n, and the function becomes

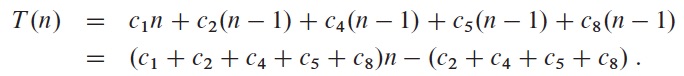
which is a linear function of n.

The worst case of the algorithm happens when the array is reverse sorted, so that t_i = i for i = 2, 3, ..., n, and the function becomes

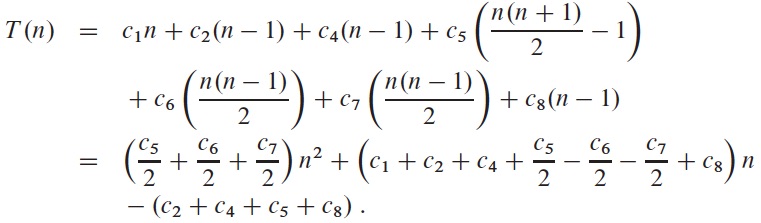
which is a quadratic function of n.

Usually, analysis of algorithm concentrates on the worst case.

5. Example: sort using a divide-and-conquer approach

1. divide the problem into a number of subproblems,
2. conquer the subproblems,
3. combine the solutions to the subproblems into the solution for the original problem.

Merge sort is an algorithm that sorts an array by cutting it into two halves, sorting them recursively, then merging the two sorted subarrays.

The merge procedures Merge(A, p, q, r) first moves the two sorted subarrays A[p : q] and A[q+1 : r] into two separate arrays L and R, put two special sentinel values at the end of each of them, then merge the two back into the original array A[p : r].

Its time expense is a linear function of n, because every data item is moved 2 times, and compared less than 1 time in average.

The following is the merge-sort algorithm.

The correctness and efficiency of this algorithm can be analyzed similarly.