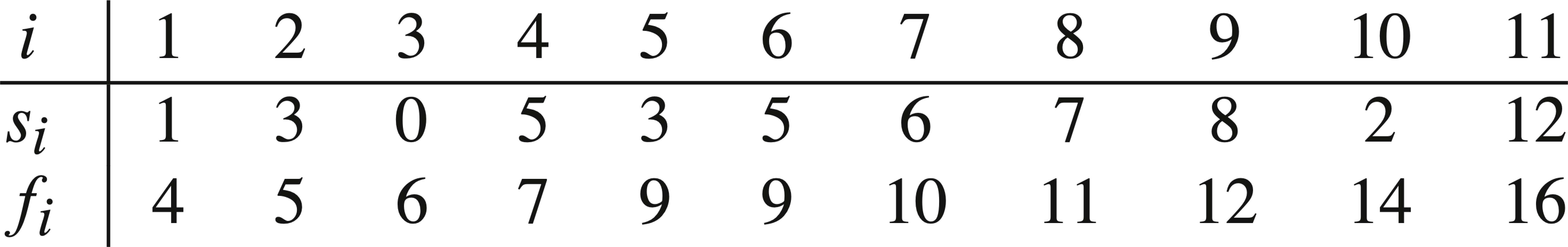
Greedy Algorithms
Take the planning matrix-chain multiplication problem as example: inspired by the first example, a greedy algorithm may "reduce" the largest dimension in each step, which in the second example leads to the solution ((A1*A2)*A3)*(A4*(A5*A6)), which is not optimal.
Unlike dynamic programming, a greedy algorithm may fail to find the optimal solution, though it often finds a reasonably good one, and runs much faster than an algorithm using dynamic programming.
A greedy solution: find the activity with the earliest finish time that is consistent with the current schedule, add it into the schedule, then recursively create the rest of the schedule.
In the following algorithm, array s and f represent the start and finish time of the activities, and they are sorted in monotonically increasingly order of finish time:
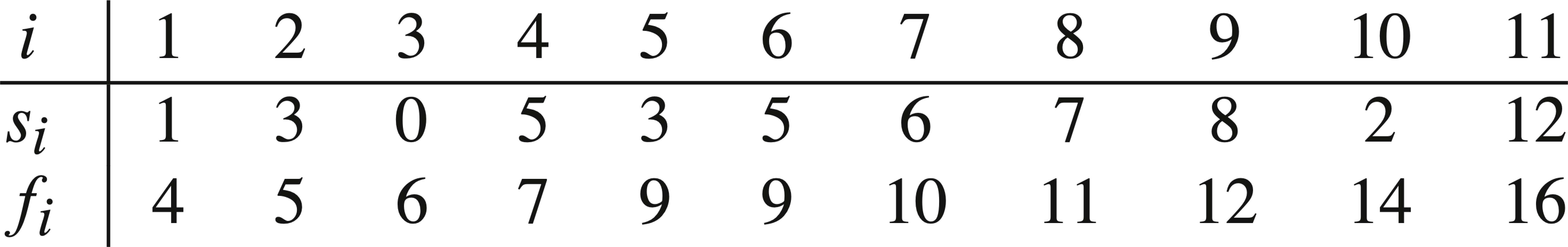
Beside the two arrays, the algorithm also takes indexes k and n as input, to indicate the range of activities to be considered. Initially, it is called as Recursively-Activity-Selector(s, f, 0, n) by algorithm Activity-Selector(s, f).
The recursive algorithm can be converted into a more efficient iterative algorithm:
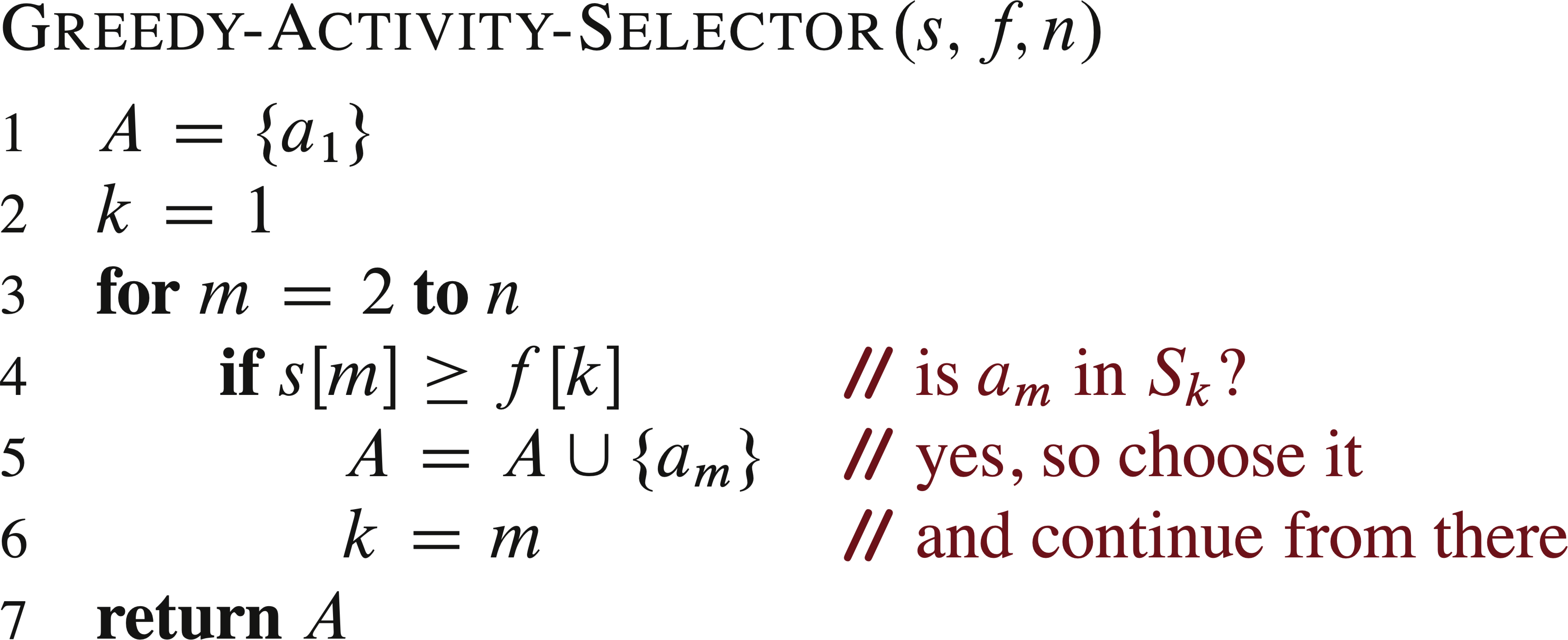
Both algorithms take Θ(n) time. The optimality of this algorithm can be proved by showing that any optimal solution can be changed into one that contains the activity with the earliest finish time.
In the following example, the variable-length codeword has an average of 2.24 bits:

Assuming binary prefix coding, a solution can be represented by a binary tree, with each leaf corresponds to an unit, and its path from root represents the code for the unit (left as 0, right as 1). An optimal code is a binary tree with the minimum expected path length from the root to the leaves.
In the following algorithm, C contains a set of units, and Q is a priority queue containing binary trees prioritized by the frequency of their roots.

Procedure HUFFMAN produces an optimal prefix code. Example:
Hill Climbing: When an optimization problem can be represented as searching for the maximum value of a function in a multidimensional space, "hill climbing" is a greedy algorithm which attempts to find a better solution by making an incremental change to the current solution.
Gradient Descent: The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent.
Best-First Search: If the next step is selected at the neighborhood of all explored points, "hill climbing" becomes "best-first search". As the selection is based on a heuristic function, it is also called heuristic search.
Real-time Computing: The response time is included in the specification of each problem instance. Time restrictions can be "hard" (as deadline) or "soft" (as degrading utility). The solution often depends hardware factors.
Anytime Algorithm: Such an algorithm improves the quality of its solution over time, and can stop at anytime with a best-so-far solution (e.g., approximating pi). An anytime algorithm no longer has a determined solution and running time for a given problem instance.
Case-by-Case Problem Solving: To solve each occurrence, or case, of a problem using currently available knowledge and resources on the case. It is different from the traditional Algorithmic Problem Solving, which applies the same algorithm to all occurrences of all problem instances. Case-by-case Problem Solving is suitable for situations where the system has no applicable algorithm for a problem as a whole, while still may solve some special cases of it. This approach gives the system flexibility, originality, and scalability, at the cost of predictability, repeatability, and terminability.