CIS 5511. Programming Techniques

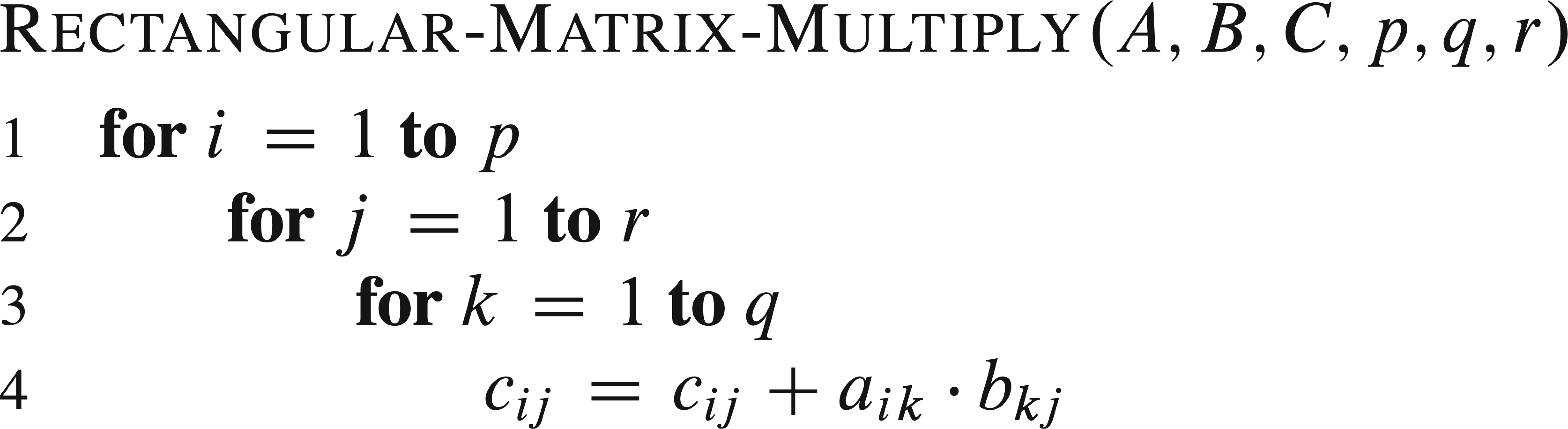
Dynamic Programming

 

1. The idea

When a problem is solved by reducing into subproblems, sometimes the same subproblem appears multiple times.

For example, Fibonacci numbers are defined by the following recurrence: 

    F(0) = 0
    F(1) = 1
    F(i) = F(i-1) + F(i-2)
It is easy to directly write a recursive algorithm according to this definition: 
    Fibonacci-R(i)
    1  if i == 0
    2      return 0
    3  if i == 1
    4      return 1
    5  return Fibonacci-R(i-1) + Fibonacci-R(i-2)
This algorithm contains repeated calculations, so is not efficient. For example, to get F(4), it calculates F(3) and F(2) separately, though in calculating F(3), F(2) is already calculated. The complexity of this algorithm is O(2n).

It is easy to see that the algorithm can be rewritten in a "bottom-up" manner with the intermediate results saved in an array. This gives us a "dynamic programming" version of the algorithm: 

Fibonacci-DP(i)
    1  A[0] = 0        // assume 0 is a valid index
    2  A[1] = 1
    3  for j = 2 to i
    4      A[j] = A[j-1] + A[j-2]
    5  return A[i]

From this simple example, we see the basic elements of dynamic programming, that is, though the solution is still defined in a "top-down" manner (from solution to subsolution), it is built in a "bottom-up" manner (from subsolution to solution). Since the subsolutions to subproblems are kept in a data structure for possible later use, each of them is only calculated once, so the complexity is O(n).

Memoization is variation of dynamic programming that keeps the efficiency, while maintaining a top-down structure. 

    Fibonacci-M(i)
    1  A[0] = 0        // assume 0 is a valid index
    2  A[1] = 1
    3  for j = 2 to i
    4      A[j] = -1
    5  Fibonacci-M2(A, i)

    Fibonacci-M2(A, i)
    1  if A[i] < 0
    2      A[i] = Fibonacci-M2(A, i-1) + Fibonacci-M2(A, i-2)
    3  return A[i]
The complexity of this algorithm is also O(n).

Dynamic programming is often used in optimization where the optimal solution corresponds to a special way to divide the problem into subproblems. When different ways of division are compared, it is quite common that some subproblems are involved in multiple times, therefore dynamic programming provides a more efficient algorithm than (direct) recursion.

The complexity of dynamic programming comes from the need of keeping intermediate results, as well as remembering the structure of the optimal solution, i.e., where the solution comes from in each step.

 

2. Example: matrix-chain multiplication

The following algorithm multiplies two matrices:

The product of a p-by-q matrix and a q-by-r matrix is a p-by-r matrix, which contains p*r elements, each calculated from q scalar multiplications and q − 1 additions. If we count the number of scalar multiplications and use it to represent running time, then for such an operation, it is p*q*r.

To calculate the product of a matrix-chain A1A2...An, n − 1 matrix multiplications are needed. Though in each step any pair of matrices can be multiplied, different choices have different costs. For matrix-chain A1A2A3, if the three have sizes 10-by-2, 2-by-20, and 20-by-5, respectively, then the cost of (A1A2)A3 is 10*2*20 + 10*20*5 = 1400, while the cost of A1(A2A3) is 2*20*5 + 10*2*5 = 300.

In general, for matrix-chain Ai...Aj where each Ak has dimensions Pk-1-by-Pk, then the minimum cost of the product m[i,j] can be obtained by looking for the best way to cut it into Ai...Ak and Ak+1...Aj. Therefore we have 

    m[i, j] = 0                                                if i = j
              min{ m[i,k] + m[k+1,j] + Pi-1PkPj }               if i < j
Since certain m[i,j] will be used again and again, we use dynamic programming to find the minimum number of operation by calculating this m value for sub-chains with increasing length, and using another matrix s to keep the cutting point k for each m[i,j].

Example: Given the following matrix dimensions:
A1 is 30-by-35
A2 is 35-by-15
A3 is 15-by-5
A4 is 5-by-10
A5 is 10-by-20
A6 is 20-by-25
P: [30, 35, 15, 5, 10, 20, 25]

then the output of the program is

which means that A1A2A3A4A5A6 should be calculated as (A1(A2A3))((A4A5)A6), and the number of scalar multiplication is 15,125.

The matrix-chain multiplication problem can be solved by either a bottom-up dynamic programming algorithm or a top-down, memoized dynamic-programming algorithm. The running time of both algorithms is Θ(n3), and the algorithm needs Θ(n2) space. Please note that this algorithm determines the best order to carry out the matrix multiplications, without doing the multiplications themselves.

 

3. Longest Common Subsequence

From a given sequence, a subsequence can be obtained by removing any number of its elements. For sequence X and Y, their Longest Common Subsequence (LCS) is not necessarily unique or continuous in either X or Y. For example, if X is ABCBDAB and Y is BDCABA, a LCS of them is BCBA with length 4, and BCAB is another one.

LCS can be recursively constructed. Let us define c[i, j] to be the length of a LCS of the sequences Xi and Yj (to index i and j in X and Y, respectively), then

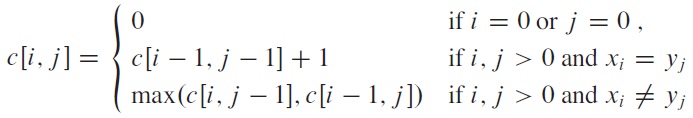
Algorithm:

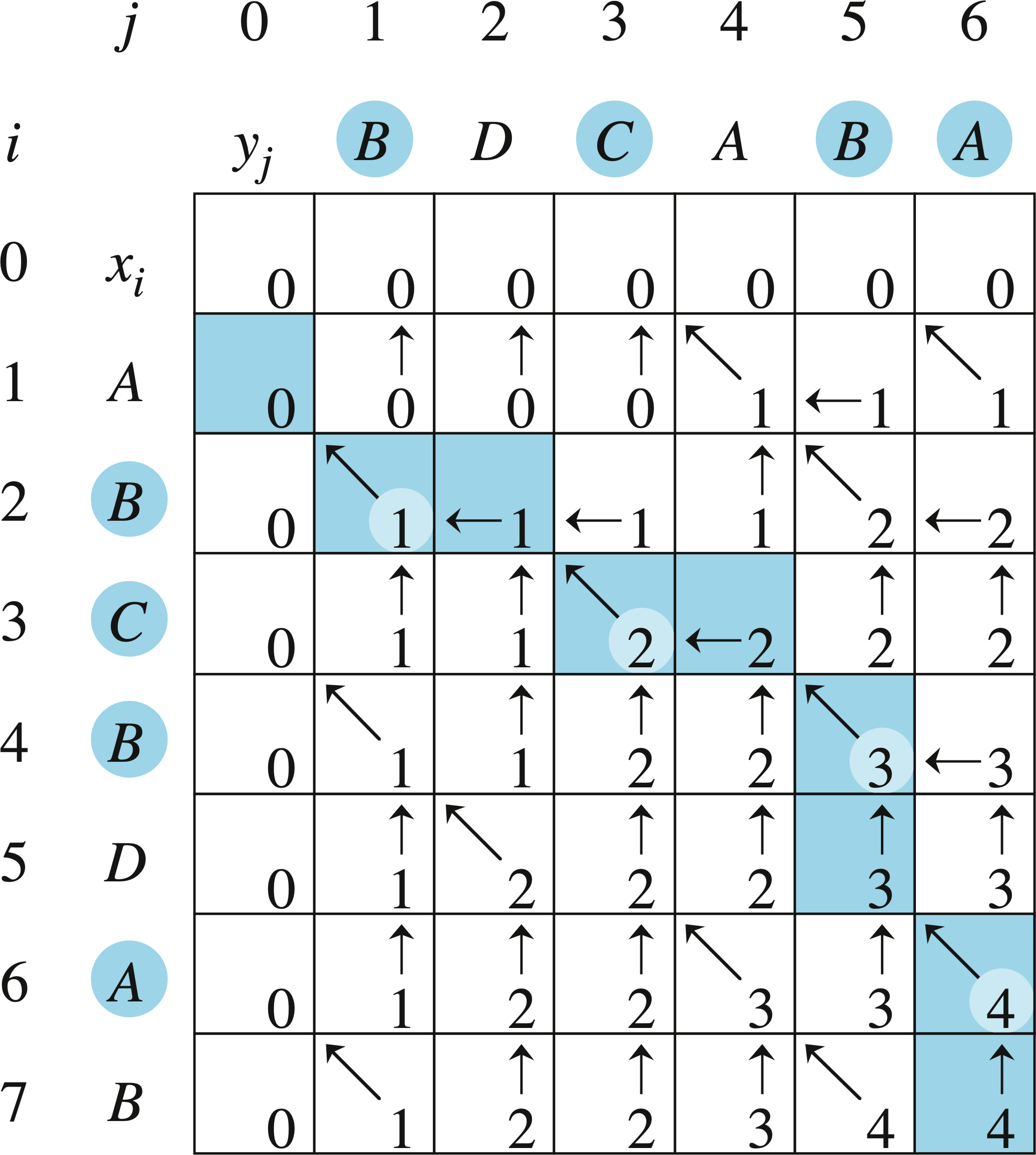
Time cost: Θ(m*n). Space cost: Θ(m*n).

Example:

 

4. Optimal Binary Search Tree

If the keys in a constant BST have different probabilities to be searched, then a balanced tree may not give the lowest average cost (though it gives the lowest worst cost). Using dynamic programming, BST with optimal average search time can be built by comparing the expected cost of each candidate (i.e., with each node as root), in a way similar to the matrix-chain multiplication algorithm. The input of this algorithm are the probabilities for each key values to be searched, as well as those of the other values not in the tree.