CIS307: SECURITY
Read Chapter 7 in Kurose-Ross's book and chapter 8 in Tanenbaum-VanSteen.
Security Threats can occur to data, hardware, software, and
communication links. Examples of security threats are
interruptions (with loss of data, denial of service),
interceptions, modifications, fabrications.
Of course we aim for
Secure Systems, with properties such as:
- secrecy (privacy, confidentiality, no eavesdropping with
consequent information leakage),
- integrity (no data tampering or other form of
vandalism),
- authentication (nobody masquerades as somebody else -
spoofing if joe@doe signs in as jane@smith - play-back attack
if a malicious user eavesdrop a message, say an encrypted password, and
plays it back -
misrepresentation if www.pinco.com responds to www.ibm.com.
A particular kind of masquerading attack is called
man-in-the-middle, whereby an interlocutor or principal,
places itself between client and server, passing back and forth messages,
after registering them and possibly modifying them). Note that authentication
usually implies timeliness: not only I want to verify that it is your message,
but also I want to be sure it is not the playback of an old message.
- non-repudiation (nobody denies its actions),
- authorization (making sure that a principal is allowed
to do what it wants to do,
using mechanisms such as Access Control Matrices,
capabilities, encryption, filtering, firewalls),
- auditing (audit-trail = analizable history of use; it establishes a basis for accountability), and
- availability, reliability, safety.
We will focus on the first four properties.
In considering security we need to distinguish what are the security policies
supported and what are the security mechanisms used to carry out the policies.
Some of the mechanisms involve:
- Cryptography, i.e. encoding information so that only the intended interlocutors
understand the transmitted information [Cryptoanalysis is the code breaker science,
and Cryptology include both].
- Message Digests, i.e. hash values computed from the message that
almost uniquely identify the message.
- Nonces, i.e. large random numbers used to make (very likely) unique
an interaction. Think of the problem of sending your encrypted password: if I
capture it then I can pass myself as you by using that encrypted password.
Examples of higher level mechanisms are:
- Digital Signatures, i.e. encoded message digests used to authenticate the sender and verify the integrity of messages. A digital signature is specific to a message.
- Certificate Authority(CA), i.e. an organization that creates and administers the distribution and use
of Digital certificates.
- Digital Certificates, i.e. data files that act like an online passport
for an internet interlocutor (people, web servers, ..). They are issued by a trusted third party, a
Certificate Authority, which verifies the identity of the certificate's holder. They cannot be forged.
Digital certificates have two purposes: to certificate their
holder, and to protect the data exchanged with that holder. A data certificate is specific to a principal,
though a principal may have a number of different digital certificates. You may hear these days
of support for e-commerce of wallets, that is components that in addition to the information
needed for a certificate, they have the information needed for the use of credit cards, plus shipping information,
etc.
- Public Key Infrastructure (PKI), i.e. the definition of the technical, operational, and legal aspects
of using a public key system to provide authentication, access control, confidentiality, and non-repudiation.
- Trusted Third party (TTP), i.e. a certificate authority, a public key infrastructure, a higher
authority that is agreed to and trusted by the communicating parties.
- Internet Messaging Security Mechanisms, i.e. mechanisms such as
the Secure Sockets Layer (SSL), a secure extension for MIME, S-Mime, and a
secure extension of HTTP, HTTPS.
There is also a Secure Electronic Transactions
(SET)
protocol and infrastructure for bank card payments over the Internet
(developed by Visa, MasterCard, etc.).
CRYPTOGRAPHY
SENDER -->message-->ENCRYPT-->encrypted-->DECRYPT-->message-->RECEIVER
message = plaintext
encrypted = cyphertext
C = E(M), E: encryption algorithm, M: Message, C: Encrypted form of message
M = D(C), D: decryption algorithm
Since good en/decryption algorithm are hard to find, and can be stolen,
people find it best to use keys in the algorithm, so that if a key
is stolen, one can choose another key, without having to invent, implement, distribute a new algorithm. So the algorithm is public (not private)
and the key is private (for now). When using keys, it is usual to write
the encoding/decoding as follows:
C = E(M, Ke), M = D(C, Kd) Ke: encryption key, Kd: decryption key
One-way function: a function that is easy to compute but difficult
to invert: F(X) is easy to compute with result Y, but given Y is
very difficult to determine X such that F(X) is Y.
Trap-door function: a one-way function that, if we know a
specific piece of information, can be inverted easily. That is the case
when we have the decryption key to decode an encrypted message.
Secure channel is a communication channel that is not
accessible to potential adversaries. An insecure channel
is one that is accessible to adversaries.
The key can be private (also called secret) or public.
If private only one program knows it. If public, any program can obtain
it, usually from an appropriate service. The longer the key, the safer
it is. Suppose that I use a key that is just one bit. It is either 0 or
1; it will not take a malicious listener long before the key is guessed!
Also, the more encrypted text is seen, the easier is to break the code
because of the statistical properties of the text being encrypted.
An encryption/decription schema is symmetric if the same key is
used for encryption and for decryption. [To be precise, en/decryption is
symmetric if there is a well defined known function for converting between
the encryption and decryption key.] It is asymmetric otherwise.
Usually symmetric algorithms are much faster than asymmetric algorithms.
Often one uses hybrid cryptography:
one uses asymmetric cryptography to obtain a key for symmetric
cryptography; this key, called a session key, remains valid only for
one limited-time communication session. Assume that we are using symmetric encryption.
Then if any two of n principals want to communicate in secrecy, we will
need O(n*n) secret keys with a gigantic problem for exchanging such keys
securely. If instead we use public key cryptography, as we will see, O(n)
secret keys will suffice.
Data Encryption Standard (DES) - secret key, symmetric.
Uses 64 bit keys (56 of information plus parity bits).
It encrypts/decrypts data in chunks that are 64 bit long. Other sizes often
used in DES are 128 (112 of information) and 192 (168 of information). As
the size of the key grows, the difficulty of breaking the code grows,
exponentially. You may want to read about
how
the C library helps you deal with DES encryption (and passwords).
An alternative to DES is IDEA (International Data Encryption
Algorithm - 128 bit keys, 64 bit encryption blocks) which is used in PGP.
The Advanced Encryption Standard (AES - 128, or 192, or 256 bit keys) is
the replacement for DES.
[In 2003 the DoD committee on National Security Systems issued a memorandum
approving the use of AES for all levels of classified information.
That would imply that AES is considered unbreakeable or at least
unbreakable by anybody with less resources than NSA.]
[DES has found new life as Triple DES: 3 DES keys are used, k1, k2,
k3. The data is encrypted first with k1, the result encrypted with k2,
the result encrypted with k3. At the decrypting end the steps are
inverted in the inverse order, first k3, then k2, then k1.]
Block Cyphers: Both DES and RSA are block cyphers, that is
the message is broken into chunks, or blocks, that are individually
encrypted. This gives rise to a problem: an attacker may infer
something about the code by looking at the individual blocks
that may be repeated in different messages or in the same message.
For this reason Cypher Block Chaining was introduced.
Diffie-Hellman (1976) introduced the concept of public keys. [Apparently,
in 1973 Clifford Cocks in England came up with the same concept
and apparently in 1970 somebody at NSA did too.] If two
interlocutors want to talk we will have a Sender and a Receiver.
The Sender will find out from a "reliable source" the public key used
by Receiver and encode the message with that key. Only the intended
receiver will know the private key and decode the message. [To answer
the Receiver will use the public key of the Sender.]
Rivest-Shamir-Adleman (RSA) (1978)
D = E, i.e. same algorithm for encryption and decryption
Ke is public, so we call it Kp
Kd is secret, so we call it Ks
----------------------------------
Choose two primes p and q, let N = p*q
We will be able to send only messages whose numeric code is < N
Choose an integer e relatively prime to (p-1)*(q-1) = Z.
Find the smallest integer d such that
(d*e)mod Z = 1
[thus d is the modular inverse of e].
Then the public key Kp is [e,N] and the private key Ks is [d,N].
e
C = M mod N //This says that the message M must be smaller
//than N. If longer, break it up into
//chunks smaller than N and encrypt them
//individually.
d
M = C mod N
Apparently, given N and e, it is computationally hard to compute d,
if N is sufficiently large [al least 512 bits]. p and q must each
be more than 200 bits.
----------------------------------
Example: p = 13, q = 17, N = 13*17 = 221, Z = (p-1)(q-1) = 192
e = 5
d = 77
The number of bits we can encrypt is 7 since
2^7 = 128 < N = 221.
So if we want to send a message longer than
7 bits we will decompose it in 7 bit fragments
and encrypt them individually.
----------------------------------
The RSA algorithm is not good for protecting
large messages since with it encryption/decryption are fairly
slow - more that 1000 slower than DES. But it can
be used to transmit essential information, such as
secret keys and passwords. [Apparently on a 175Mhz Alpha
RSA encrypts 1kbps, while 56-bit DES encodes over 30Mbps.]
In RSA it is normal to use 512-bit and 1024-bit keys.
Secrecy: Principal A wants to send a secret message M to principal
B. [It is usual in the security area to use names like Alice and
Bob for the principals involved in the interaction.]
Let Kp(B) be the public key of B, Ks(B) the secret key of B.
A will send E(M, Kp(B)). B is the only one with
Ks(B), thus it is the only one who can read the message.
A --> E(M, Kp(B)) --> B
The Key distribution problem for public and private keys
is dealt with through a Public Key Infrastructure and the use of
digital certificates.
One-Time Pad: There is a an encryption method that is
unbreakable, but very inconvenient.
Suppose that we know that we need to send from A to B
a message of n bits. We give before hand to both A and B
a pad string s of n bits randomly generated. Then
A will encrypt his message M as M^s, where ^ means exclusive or.
And B will decrypt the encrypted message E with E^s.
The trick is that, take a message bit x and a pad bit y, we have
x^y^y = x = y^y^x
Try it for any of the values of x and y and you will see it is true.
The one-time pad is called one-time for a good reason.
Suppose that I use it on two messages, so PAD ^ MESSAGE1 and PAD ^ MESSAGE2.
If I do the exclusive or of these two encrypted messages PAD is eliminated and I get
MESSAGE1 ^ MESSAGE2. If I know either I can derive the other, and in any case
now decrypting becomeseasier because we may have good idea on possible
messages thus the search is reduced.
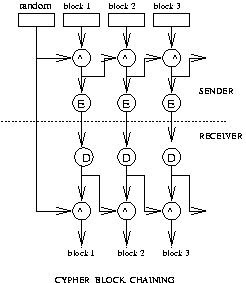
Cypher Block Chaining (CBC): Each message is started with
an extra block, say, the current daytime, which makes the block
unique. This plaintext block is not encrypted and sent as is.
For all successive
plaintext block, before encryption we will XOR it with the
encrypted block of the preceding (except first) plaintext block.
At the receiver
after the first cypher block, for all other cypher
blocks, after decryption, we will XOR them with the preceding
undecrypted cypher block. Note that block-chaining makes it harder
to break a code, but in the case of errors, not just the block
where the error occurred gets messed up, but also the blocks that follow.
Stream Cyphers: For the transmission of phone conversations,
for efficiency reasons, instead of block cyphers are used cyphers
that encrypt messages incrementally one symbol (may be one bit) at
a time. A frequently used technique is to xor (like
in one-time pad) the streamed data with an
appropriately generated binary stream (usually a sequence of random numbers
starting with an initial seed agreed to by sender and receiver0.
An example of stream cypher is RC4, due to Rivest, one of the authors
of RSA. It uses a 256 byte key R (there is a way to generate such a key from ordinary
smaller keys if desired) to generate a sequence of bytes that will
be Xor-ed with the plaintext stream to generate the cypher stream. The
algorithm goes as follows:
unsigned char nextPadByte() {
static int p = 0;
static int q = 0;
p = (p+1)%256;
q = (q+R[p])%256;
unsigned char temp = R[p]; R[p] = R[q]; R[q] = temp;
return R[R[p]+R[q]%256];
}
which generates successive bytes of the one-time pad for as long as it is
needed. RC4 is used for instance in SSL and WEP.
Steganography: On a totally different plane, a secret
message may be superimposed on a visible message. For example,
in an image where color is encoded as a 24bit number using
RGB coding (one byte per color), we may use one bit from each
color to send a message. The change in the picture would be
not easily detectable, and we could transmit a secret message.
[In a picture with 100,000 pixels, we would have 300,000 bits,
i.e. 7,500 bytes available for our secret message.]
We could get even less detectable changes by pre-agreeing
on a random generated sequence (say, with given seed), computing
from it a probabily, and then changing only the bytes for
which the probability is above a chosen threshold.
Of course we could also hide a message in transmitted music or voice.
But in this case the available data rate for the hidden channel will be
smaller. Note that sound and images are often transmitted using
lossy compression/uncompression schemes. The hidden communication may
use forward error correction to get around this problem.
Another use of steganography is in watermarking.
You record music or video using MPEG-3 or MPEG-4. You want to be
able to determine if a given CD or DVD has been copied from your
original. You insert in the record watermarks, extra data that
does not change the quality of the record, but identifies it.
Diffie-Hellman Key Exchange protocol
We want A and B to come up an agreed upon secret key without exchanging data
that bad guys can use to determine the secret key.
A choses a very large prime number p and A also chooses a very large number g which is a
primitive root modulo p (i.e., for every number n equal 1, 2, .. p-1, there is a number k
such that gkmod p is equal to n).
They make public these numbers. Then A choses a large integer x and keeps it secret.
Similarly B choses a large integer y and keeps it secret. Then they go thru the following steps:
- A sends to B gxmod p
- B sends to A gymod p
It is considered computationally hard (impossible) given g, p, and gx mod p
to compute x (similarly for y).
Now A computes (gymod p)x. It is equal to gxymod p.
Now B computes (gxmod p)y. It is equal to
gxymod p.
Thus both A and B have the value gxymod p that is not known by anybody else.
A and B can use this value as their secret key.
For example p = 23, g = 5; x = 6; then A computes
gxmod p = 56mod 23 = 8.
B chooses y = 15 and computes gymod 23 = 515 mod 23 = 19.
Then A computes 196mod 23 = 2 and B computes 815mod 23 = 2.
A and B have reached the same result!
Diffie-Hellman is vulnerable to man-in-the-middle attack if the identities of the two principals are
not authenticated.
Shamir's Sharing a Secret Problem, and Solution
Shamir of RSA fame proposed the following problem: n people share a secret D (say, the
combination for opening a bank's vault). They do not trust each other so they want to be sure
that D can be determined if at least k of them agree. Here is the suggested solution:
- Compute at random large numbers
a1, a2, .., ak-1
- Let y(x) be the polynomial D + a1 x + a2 x2 +
ak-1 x k-1
- Give to person j, for j from 1 to n, the value y(j)
- Since a polynomial of degree k-1 is fully determined when we are given k distinct values of
the polynomial, it follows that when k people get together they can determine the polynomial,
thus can compute D (the value of y at 0).
DIGITAL SIGNATURES and DIGEST FUNCTIONS (Integrity)
User A writes a document M, wants to distribute it
and be sure that
- all receivers R are sure that the document is the unmodified original one
(integrity, no tampering),
- it has been sent by A (no impersonation), and
- A cannot deny having sent it (non-repudiation).
A does not care who or how many principals(programs/people) read the message.
Digest Function: a function that, given a document M
generates a brief "fingerprint" or "message digest" or "hash value"
or "thumbprint" that identifies this document uniquely with almost
certainty.
A digest function must be secure, so that we cannot
from the digest determine the message that produced it, and must
avoid "collisions": it must be computationally unfeasible, given
a message, to find another message that generates the same digest.
MD5 (Rivest, 1992): A digest function that
generates a 128 bit
fingerprint from its text argument. It is much quicker to compute than
encrypting with DES [on a 175Mhz Alpha, MD5 digest is computed at
over 80Mbps]. Now the most frequently used digest function is
SHA-1,
which is more secure than MD5 and
generates a 160 bit fingerprint from its text argument. For simplicity
we use MD5 to refer to a generic hash function.
A sends:
M + E(MD5(M), Ks(A)) // Ks(A) = Secret key of A
['+' means concatenation, E(MD5(M), Ks(A)) is called the digital signature of the
message. It is also often called a Message Authentication Code (MAC) if obtained
using secret key cryptography.]
R uses the identity of A to determine the public key of A.
R uses this public key of A to decrypt the "digital signature" of M and obtain the hash value MD5(M).
R uses the Digest Function to compute the hash value of M.
If the two hash values are the same, all is well. Otherwise message was corrupted
or not sent by A.
A ----> M + E(MD5(M), Ks(A)) ---> B
If in addition to authentication and integrity we also
want secrecy then the message sent will be
A ----> E(M + E(MD5(M), Ks(A)), Kp(B)) ---> B
A weakness of the use of digital signatures is that it requires
knowledge of the public key of the interlocutors.
The danger is impersonation - if
there is no reliable way of distributing public keys. The solution, as we will see
later, is to use digital certificates and certificate authorities.
We have observed that with a digital signature we also achieve
non-repudiation since using public-key cryptography only the sender may
have created such a signature. If we had used secret key cryptography that
would be lost since now both the sender and the receiver could have
created the signature.
Using PGP to send a message
Suppose that A wants to send message M to B using PGP.
A obtains Kp(B) from some trusted public directory.
PGP computes a 128 bit long random sequence K that will be used as
IDEA session key. Then
A --> RSA(K, Kp(B)) + IDEA(M, K) --> B
Now B decrypts K by using RSA and his private key, then uses IDEA
with the session key K to decrypt M. Assuming that the public key being used
for B is truly of B, then only B will be able to read, and fast, the message
M. Of course this does nothing that authenticates A as sender of the
message.
Notice that we are sending a secret message only to B at the speed of IDEA
(fast) and with the safety of RSA (high). It is one of those rare cases
where we can get the best of two worlds - like a cheap ($12K) new Mercedes!
Alternative codes fast/reliable
could be used in place of IDEA/RSA to achieve the same effect.
Attempts at Authentication
Principal A wants to authenticate itself
to other principals. Let Kp(A) be the public key of A, Ks(A) the
secret key of A.
A will append E(A_id, Ks(A)) to its messages.
Any principal B that receives this information will use Kp(A)
to decode the signature, if it succeeds and finds "A_id",
it will "know" that only A could have sent the message.
In the following we use "+" to express "concatenation".
A --> A_id + E(A_id, Ks(A)) --> B
Note that this authentication, as it stands, is dangerous: somebody
could capture and save that message (A_id+E(A_id,Ks(A))), and then use
it to impersonate A by playing back (playback attack) a previous authentication message.
We can solve the problem as follows: when A wants to authenticate itself
to B, it asks B to send first to A a string x which is likely being sent
for the first time to A (choose x at random as a 100 digits number!
such a number is usually called a nonce). Then A
sends to B
A_id + E(A_id + x, Ks(A))
now nobody can have memorized the authentication message and play it back.
Note that also this authentication is dangerous if anybody, not just B, could
have sent to A the nonce x. Because then C could impersonate A in interacting
with B. It gets in the middle between A and B. Waits for A to make a request to B
and intercepts the communication.
A --> A_id --> C --> A_id --> B
A <-- x <-- C <-- x <-- B
A --> E(A_id + x, Ks(A)) --> C --> E(A_id + x, Ks(A)) --> B
and now B believes that C is really A, while A just thinks the
communication was lost. If the communication from now on is in
plaintext then C will be able
to talk with B impersonating A.
We get back to this later. This is a form of
man-in-the-middle.
attack. Later we will see another form.
Direct Authentication and Session Key exchange (using symmetric key)
We want a client to authenticate its identity to the server and the server
to authenticate its identity to the client. We assume that the true client and server
share a secret password P from which plus userId an algorithm can compute a key K.
We use the notation K(Client) and K(Server) to indicate the
value of K as assumed respectively by the client and the server. We should have K = K(Client) = K(Server).
[Instead of a protocol based on symmetric cryptography,
we could have used a protocol based on asymmetryc cryptography.]
- The client sends to the server the message
clientId
- The server selects at random an integer x [it is random so that likely it
was not used before] and sends to the client the message
x
- The client uses K(Client) to encode the message received,
selects at random a number y, and sends to the server the message
E(x, K(client)) + y
- At this point, if x is retrieved, the server is certain of the identity
of the client. Now the server sends to the client the message
E(y, K(server))
- The client uses K(Client) to decode the message. If y is
retrieved, the client is certain of the identity of the server.
Mutual authentication has been achieved.
If desired at this point the server can send to the client the message
E(SK, K(server))
where SK is the session key that the server and client can use
to exchange information during this session.
Note that only the specified client will be able to decode the session key.
This session key will be valid only for a specified time interval.
The fact that K is used only during the exchange that results
in the sharing of the session key SK, makes it more difficult for an hostile party to guess K.
Notice also that we have shown the case of the server giving to the client
the session key. The viceversa, with the client selecting the session key
and giving it to the server is also possible.
As already observed, nonces like x and y are used so that an intruder cannot
imitate an interlocutor by just remembering what that interlocutor
returned in another occasion (play-back attack).
Access to Protected Pages with HTTP
Nonces are used to authenticate requestors of protected
pages when using HTTP. Here are
portions of such an authentication interaction.
Portion of request from client:
GET /protected/page.html HTTP/1.1
Host: www.securesite.com
Portion of response from server:
HTTP/1.1 401 Unauthorized
WWW-Authenticate: Digest
nonce="754f34bd2a93c53762a73c175e376136"
Portion of new request from client:
GET /protected/page.html HTTP/1.1
Host: www.securesite.com
Authorization: Digest
username="giorgio"
nonce="754f34bd2a93c53762a73c175e376136"
response="4e7318ac52a625c148c41c4d525153fa"
where the response has been computed (MD5) from username, password, nonce,
hostname, page id. This is a challenge-response authentication,
no password is transmitted in plaintext or encoded.
Passwords and Logging-In Locally
Information about users and their passwords in Unix is usually in /etc/passwd where
passwords are displayed in encrypted form. The various fields of this file can be retrieved
with functions like getpwnam, getpwuid. The fact that the password file is public
makes it subject to a dictionary attack. An attacker can retrieve the file
and then encrypt all sorts of possible words and see if they match any of the users's
encrypted passwords.
To reduce the possibility of this attack a number of things are used.
First of all, in the /etc/passwd file it is not stored the encrypted password.
It is kept instead in the /etc/shadow file which is readable only by the root. A function
for accessing (only for root) information from the /etc/shadow file is getspnam.
[Of course, if the system is not physically protected, it may be rebooted and a
new root established.]
Another way to reduce attacks on passwords is the use of salt. We will only
consider the use of salt with MD5 encryption.
The function
char *crypt(const char *key, const char *salt);
is used to encrypt the password key with the specified salt. The value returned
has the following form (we are using an MD5 salt):
$1$yhP7/vfz$nvK0nYESg852hEX2F6Sfm1
where $1$yhP7/vfz$ is the salt that was used in crypt. In it the first 3 characters ($1$) and
last ($) indicate that we want MD5 encrypting. The value returned is saved in the
shadow file. Notice that the value thus saved contains the salt for this user.
By the way, the user can be prompted for a
password using the getpass function. Suppose that we currently have in the variable oldpass
the
value shown above ($1$yhP7/vfz$nvK0nYESg852hEX2F6Sfm1), then we can retrieve and verify the
user password with
char *newpass = crypt(getpass(), oldpass);
then if oldpass and newpass are equal, the user is who he says he is. Salt, when the user
password is first encrypted, should be a random value.
The use of a fixed value, say all zeros, would defeat its purpose. The salt is
essentially a small nonce.
Passwords and Logging-In Remotely
If we are logging in remotely we do not want to transmit passwords on the wire. If I use
telnet my password will travel as text on the line. Wicked people with things like ethereal
will be able to pick it up with ease.
There is first the problem of how the password is initially set up and shared.
For this we can use either a separate secure channel, or we use the Diffie-Hellman scheme.
If we assume that attackers can read what is being communicated,
but not insert data themselves, then we
can do as follows [we assume that B is really B].
(1) A obtains the public key of B (2) A sends to B its id (3) B sends to A a
nonce x (4) A sends to B E(A+x+password, Kp(B)) where password is the password that A wants to
establish with B.
Once the password is stored at both A and B,
A cannot log-in to B by just sending the encrypted password because that opens them to a
playback attack.
From now on we do not want to transmit the password either as plaintext or as
cyphertext.
We need to have a challenge-response protocol: the server sends a nonce to the client,
the client creates a digest combining the id of the client, the password, and the nonce.
Since the server has the same information as the client it can verify if the digest
received from the client is correct.
Direct exchanges of public keys: Man-in-the-Middle Attack
Alice and Bob are friends and want to communicate
with absolute secrecy.
They agree to exchange, say by email, public keys while authenticating
each other.
At the time that the public keys are exchanged a malicious third-party,
Mallory does the following:
Alice --> Alice_id --> Mallory --> Alice_id --> Bob
Mallory <-- x <-- Bob
Mallory --> E(x, Ks(Mallory)) --> Bob
Mallory <-- send me your public key <-- Bob
Mallory --> Public_key_of_Mallory --> Bob
Bob now thinks Mallory is Alice since
it can decrypt E(x,Ks(Mallory))
Alice <-- x <-- Mallory
Alice --> E(x, Ks(Alice)) --> Mallory
Alice <-- Send me your public key <-- Mallory
Alice --> Public_key_of_Alice --> Mallory
Now Alice has authenticated herself to Mallory.
Alice <-- Bob_id <-- Mallory
Alice --> y --> Mallory
Alice <-- E(y, Ks(Mallory)) <-- Mallory
Alice --> Send me your public key --> Mallory
Alice <-- Public_key_of_Mallory <-- Mallory
Alice now thinks that Mallory is bob since it
can decrypt E(y,Ks(Mallory))
When Bob sends data d to Alice it sends
E(d, Public_key_of_Mallory)
Mallory decrypts and sends to Alice
E(d, Public_key_of_Alice)
and similarly in the opposite direction.
From this moment on everything exchanged by Alice and Bob gets interpreted
by Mallory even if encrypted. Clearly the idea of exchanging naively
public keys is no good.
Some certified way of exchanging public keys is required, a public-key
infrastructure.
Authentication Server and Distribution of Session Key
Here is an
Authentication protocol (modified from a protocol by Needham - Schroeder,
and related to Kerberos) used when
there is an Authentication Authority S
that generates session keys for interaction between two
interlocutors A and B. It is carried out
when a
Client A wants
to communicate with a server B. It is assumed that the authentication server
and A share a secret key K(A) and the authentication server and B share a
secret key K(B). Usually
these secret keys are computed from userid, password pairs.
[This protocol could be adopted in a Napster like system to achieve security in
the interaction between peers.]
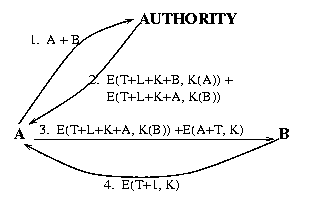
- A sends to S the cleartext message
A + B
to mean that A wants to interact with B.
- S generates a timestamp T, a duration L (Lifetime), and a session key K
and sends to A the message:
E(T + L + K + B, K(A)) + E(T + L + K + A, K(B))
- Now A uses its key K(A) to obtain the session key K, plus T and L; it
then sends to B the message
E(T + L + K + A, K(B)) + E(A + T, K)
- B uses K(B) to determine T, L, K and A.
The E(A + T, K) part is necessary to authenticate that the message
is really from A (only A can have obtained the session key K, as
demonstrated by the A+T value) and not from somebody that eavesdropped the
conversion between S and A and obtained the E(T + L + K + A, K(B)) part.
For this reason the E(A+T,K) part is called an authenticator.
Now also B has the session key K, plus T and L, and knows that
it can interact with A. It does so by sending to A the message
E(T+1, K)
to indicate that B is ready. This authenticates B to A since only B has
the session key K, as demonstrated by T+1.
Zero-Knowledge Proofs and Authentication
Public key cryptography has as weakness the problem of distributing safely
public keys. There are ideas going by the name of Zero-Knowledge
proofs, that may go around this problem, especially for problems of authentication.
Here is an example of what we mean by zero knowledge proof.
Suppose that Peggy wants to prove to Victor that she knows a magical incantation (say
abracadabra) for opening a door but does not want Victor to learn that incantation. That is
Peggy wants to prove to Victor that she has some knowledge without Victor learning that
knowledge. We can assume the following arrangement:
+------------+--------------+
| | Peggy |
| +--------+----------+ |
| | | |
| A | | B |
| +-------------------+ |
| |
+----------- -------------+
Victor
Victor does not know if Peggy is in the A or B corridor. Victor chooses at random
a corridor X (either A or B) and says to Peggy to come out thru corridor X. If
Peggy actually does come out thru corridor X the Victor can assume with 50% probability that
Peggy knows the incantation. If this game is played 20 times and each time Peggy comes out
from the correct corridor, then Victor is certain that Peggy knows the incantation with
1/1000000 probability of error. Notice that Victor has no no further knowledge about the
incantation.
The idea of zero-knowledge proofs, originally introduced by Goldwasser, Micali, and
Rackoff, was applied to the problem of authentication by
Fiat and Shamir
using number theory.
More About Digital Certificates, Certificate Authorities, and SSL
As already indicated, a digital certificate is associated with an
internet interlocutor to make secure its interactions with other interlocutors.
At a minimum a digital certificate will include:
- Name and Digital certificate of the certification authority that issued
this certificate
- The name and the public key of the owner of the certificate
- Serial number and expiration date of the certificate.
In addition it may contain also the owner's address, e-mail address, phone,
etc. The certificate is encoded by the issuing certificate authority using its
private key so that the content of the certificate cannot be tampered
with without detection.
Here is how the certificate works. The sender requests the certificate
of the recipient from the CA. This certificate is encrypted with the CA's
secret key and contains the recipients's public key and additional
information. The sender decodes the certificate with the
public key of the CA and encodes the message with the retrieved public key
of the receiver.
The standard for Digital Certificates is
X.509.
The public keys of a number of certification authorities are built in our
web browsers so that the browser can appropriately process certificates.
A message M can be sent as follows:
M + DigitalSignatureOfM + DigitalCertificateOfSender
and, if the certification authority is reliable, we are guaranteed
authentication and non-tampering. Thus digital certificates can be used
in place of passwords to identify principals. If in addition to
authentication and integrity we want secrecy, it is easy to do since the
DigitalCertificateOfReceiver contains the Public_key_Of_Receiver. Thus we send
E(M+DigitalSignatureOfM, Public_key_Of_Receiver) +
DigitalCertificateOfSender
A Certificate Authority, in addition to issuing certificates, will be
concerned with
renewing (i.e. extend the duration), and revoking
(i.e. terminating the
validity) existing certificates.
A Certificate Authority cannot appear as a single server to which all
users make appeal. Instead, as in the case of DSN (Distributed Name Service)
one needs a distributed structure of communicating certificate authorities.
At present there are a number of competing certificate authority services
and a server used in e-commerce
will have to keep certificates for the certification services it trusts.
Front ends to certificate authorities are often called Registration
Authorities.
SSL, the Secure Socket Layer, acts as an intermediate layer between the
application protocol, say HTTP, and the
transport protocol, say TCP. SSL has two subprotocols.
One specifies the format of the messages exchanged. The other specifies the
handshakes taking place between clients
and servers. The protocol allows the selection of the cryptographic
algorithm used. It always requires authentication
of the server. Authentication of the client is optional. [Server
authentication is almost always crucial - think of
client having to give to server its own visa card number - and it is done
using certificate. Client
authentication is rarer - necessary, for instance,
if client asks for bank balance; not necessary if client asks for today's
weather. In the case that the client
gives a credit card number, the application using SSL will have other
methods to make sure that the client is
who it claims to be.]
In their SSL interactions interlocutors use digital signatures, digital
certificates, and rely on certificate authorities. They use random numbers
(nonces) to eliminate the possibility of hostile interlocutors remembering
old interactions.
Communications between client and server are encrypted.
Public key cryptography is used only during session setup: the client,
usually a browser, selects a secret symmetric session key,
encrypts it with the public key of the server, and sends it to
the server. Afterwards client and server communicate with the
selected secret session key.
SSL has been modified into an Internet standard, the Transport Layer Security
(TLS) protocol, as expressed in
RFC 2246
A standard for e-commerce secure transactions is
SET.
It makes for interesting reading, which, in the case of the
business description,
is also easy.
The library openssl lets us use
cryptographic tools at various levels, defining our own protocols, or relying on
SSL.

