SECURE HASH STANDARD
Explanation: This Standard
specifies a Secure Hash Algorithm, SHA-1, for computing a condensed
representation of a message or a data file. When a message of any length <
264 bits is input, the SHA-1 produces a 160-bit
output called a message digest. The message digest can then be input to the
Digital Signature Algorithm (DSA) which generates or verifies the signature for
the message. Signing the message digest rather than the message often improves
the efficiency of the process because the message digest is usually much smaller
in size than the message. The same hash algorithm must be used by the verifier
of a digital signature as was used by the creator of the digital signature.
The SHA-1 is called secure because it is computationally infeasible to
find a message which corresponds to a given message digest, or to find two
different messages which produce the same message digest. Any change to a
message in transit will, with very high probability, result in a different
message digest, and the signature will fail to verify. The SHA-1 is based on principles similar to those
used by Professor Ronald L. Rivest of MIT when designing the MD4 message digest
algorithm ("The MD4 Message Digest Algorithm," Advances in Cryptology - CRYPTO
'90 Proceedings, Springer-Verlag, 1991, pp. 303-311), and is closely modelled
after that algorithm.
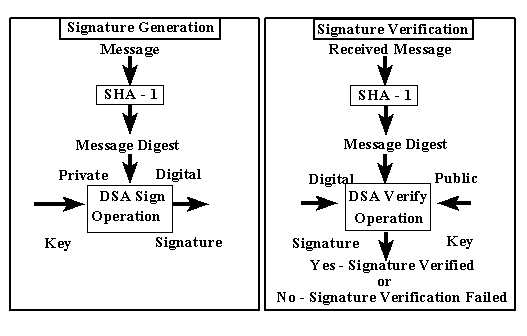
Figure 1:
Using the SHA-1 with the DSA
Applications: The SHA-1 may be used with the
DSA in electronic mail, electronic funds transfer, software distribution, data
storage, and other applications which require data integrity assurance and data
origin authentication. The SHA-1 may also be used whenever it is necessary to
generate a condensed version of a message.
Objectives: The objectives of this standard are to:
- a. Specify the secure hash algorithm required for use with the Digital
Signature Standard (FIPS 186) in the generation and verification of digital
signatures;
- b. Specify the secure hash algorithm to be used whenever a secure hash
algorithm is required for Federal applications; and
- c. Encourage the adoption and use of the specified secure hash algorithm
by private and commercial organizations.
1. INTRODUCTION
The Secure Hash Algorithm
(SHA-1) is required for use with the Digital Signature Algorithm (DSA) as
specified in the Digital Signature Standard (DSS) and whenever a secure hash
algorithm is required for federal applica- tions. For a message of length <
2^64 bits, the SHA-1 produces a 160-bit condensed representation of the
message called a message digest. The message digest is used during generation
of a signature for the message. The SHA-1 is also used to compute a message
digest for the received version of the message during the process of verifying
the signature. Any change to the message in transit will, with very high
probability, result in a different message digest, and the signature will fail
to verify.
The SHA-1 is designed to have the following properties: it
is computationally infeasible to find a message which corresponds to a given
message digest, or to find two different messages which produce the same
message digest.
2. BIT STRINGS AND INTEGERS
The following
terminology related to bit strings and integers will be used:
- a. A hex digit is an element of the set {0, 1, ... , 9, A, ... , F}. A
hex digit is the representation of a 4-bit string. Examples: 7 =
0111, A = 1010.
- b. A word equals a 32-bit string which may be represented as a sequence
of 8 hex digits. To convert a word to 8 hex digits each 4-bit string is
converted to its hex equivalent as described in (a) above. Example:
1010 0001 0000 0011 1111 1110 0010 0011 = A103FE23.
- c. An integer between 0 and 232 - 1
inclusive may be represented as a word. The least significant four bits of
the integer are represented by the right-most hex digit of the word
representation. Example: the integer 291 = 28+25+21+20 = 256+32+2+1 is
represented by the hex word, 00000123.
- If z is an integer, 0 <= z < 264,
then z = 232x + y where 0 <= x <
232 and 0 <= y < 232. Since x and y can be represented as words X and Y,
respectively, z can be represented as the pair of words (X,Y).
- d. block = 512-bit string. A block (e.g., B) may be represented as a
sequence of 16 words.
3. OPERATIONS ON WORDS
The following logical
operators will be applied to words:
- a. Bitwise logical word operations
X ^ Y = bitwise logical "and" of X and Y.
X \/ Y = bitwise logical "inclusive-or" of X and Y.
X XOR Y = bitwise logical "exclusive-or" of X and Y.
~ X = bitwise logical "complement" of X.
- Example:
01101100101110011101001001111011
XOR 01100101110000010110100110110111
--------------------------------
= 00001001011110001011101111001100
- b. The operation X + Y is defined as follows: words X and Y represent
integers x and y, where 0 <= x < 232
and 0 <= y < 232. For positive integers
n and m, let n mod m be the remainder upon dividing n by m. Compute
- z = (x + y) mod 232.
- Then 0 <= z < 232. Convert z to a
word, Z, and define Z = X + Y.
- c. The circular left shift operation Sn(X), where X is a word and n is an integer with 0 <=
n 32, is defined by
- Sn(X) = (X << n) OR (X >>
32-n).
- In the above, X << n is obtained as follows: discard the left-most
n bits of X and then pad the result with n zeroes on the right (the result
will still be 32 bits). X >> n is obtained by discarding the
right-most n bits of X and then padding the result with n zeroes on the
left. Thus Sn(X) is equivalent to a circular
shift of X by n positions to the left.
4. MESSAGE PADDING
The SHA-1 is used to compute
a message digest for a message or data file that is provided as input. The
message or data file should be considered to be a bit string. The length of
the message is the number of bits in the message (the empty message has length
0). If the number of bits in a message is a multiple of 8, for compactness we
can represent the message in hex. The purpose of message padding is to make
the total length of a padded message a multiple of 512. The SHA-1 sequentially
processes blocks of 512 bits when computing the message digest. The following
specifies how this padding shall be performed. As a summary, a "1" followed by
m "0"s followed by a 64-bit integer are appended to the end of the message to
produce a padded message of length 512 * n. The 64-bit integer is l, the
length of the original message. The padded message is then processed by the
SHA-1 as n 512-bit blocks.
Suppose a message has length l <
264. Before it is input to the SHA-1, the
message is padded on the right as follows:
- a. "1" is appended. Example: if the original message is
"01010000", this is padded to "010100001".
- b. "0"s are appended. The number of "0"s will depend on the original
length of the message. The last 64 bits of the last 512-bit block are
reserved for the length l of the original message.
- Example: Suppose the original message is the bit string
01100001 01100010 01100011 01100100 01100101.
- After step (a) this gives
01100001 01100010 01100011 01100100 01100101 1.
- Since l = 40, the number of bits in the above is 41 and 407 "0"s are
appended, making the total now 448. This gives (in hex)
- 61626364 65800000 00000000 00000000
- 00000000 00000000 00000000 00000000
- 00000000 00000000 00000000 00000000
- 00000000 00000000.
- c. Obtain the 2-word representation of l, the number of bits in the
original message. If l < 232 then the
first word is all zeroes. Append these two words to the padded message.
- Example: Suppose the original message is as in (b). Then l =
40 (note that l is computed before any padding). The two-word
representation of 40 is hex 00000000 00000028. Hence the final padded
message is hex
- 61626364 65800000 00000000 00000000
- 00000000 00000000 00000000 00000000
- 00000000 00000000 00000000 00000000
- 00000000 00000000 00000000 00000028.
The
padded message will contain 16 * n words for some n > 0. The padded
message is regarded as a sequence of n blocks M1 , M2, ... ,
Mn, where each Mi contains 16 words and M1 contains the first characters (or bits) of the
message.
5. FUNCTIONS USED
A sequence of logical
functions f0, f1,..., f79 is used in
the SHA-1. Each ft, 0 <= t <= 79,
operates on three 32-bit words B, C, D and produces a 32-bit word as
output. ft(B,C,D) is defined as follows:
for words B, C, D,
- ft(B,C,D) = (B AND C) OR ((NOT B) AND
D) ( 0 <= t <= 19)
- ft(B,C,D) = B XOR C XOR D (20 <= t
<= 39)
- ft(B,C,D) = (B AND C) OR (B AND D) OR
(C AND D) (40 <= t <= 59)
- ft(B,C,D) = B XOR C XOR D (60 <= t
<= 79).
6. CONSTANTS USED
A sequence of constant
words K(0), K(1), ... , K(79) is used in the SHA-1. In hex these are given
by
- K = 5A827999 ( 0 <= t <= 19)
- Kt = 6ED9EBA1 (20 <= t <= 39)
- Kt = 8F1BBCDC (40 <= t <= 59)
- Kt = CA62C1D6 (60 <= t <= 79).
7. COMPUTING THE MESSAGE DIGEST
The message
digest is computed using the final padded message. The computation uses
two buffers, each consisting of five 32-bit words, and a sequence of
eighty 32-bit words. The words of the first 5-word buffer are labeled
A,B,C,D,E. The words of the second 5-word buffer are labeled H0, H1, H2, H3, H4. The words of the 80-word sequence are labeled
W0, W1,...,
W79. A single word buffer TEMP is also
employed.
To generate the message digest, the 16-word blocks
M1, M2,...,
Mn defined in Section 4 are processed in
order. The processing of each Mi involves
80 steps.
Before processing any blocks, the {Hi} are initialized as follows: in hex,
- H0 = 67452301
- H1 = EFCDAB89
- H2 = 98BADCFE
- H3 = 10325476
- H4 = C3D2E1F0.
Now
M1, M2, ...
, Mn are processed. To process Mi, we proceed as follows:
- a. Divide Mi into 16 words
W0, W1,
... , W15, where W0 is the left-most word.
- b. For t = 16 to 79 let Wt =
S1(Wt-3
XOR Wt-8 XOR Wt-
14 XOR Wt-16).
- c. Let A = H0, B = H1, C = H2, D =
H3, E = H4.
- d. For t = 0 to 79 do
- TEMP = S5(A) + ft(B,C,D) + E + Wt +
Kt;
- E = D; D = C; C = S30(B); B = A; A
= TEMP;
- e. Let H0 = H0 + A, H1 =
H1 + B, H2
= H2 + C, H3 = H3 + D,
H4 = H4 +
E.
After processing Mn, the
message digest is the 160-bit string represented by the 5 words
- H0 H1
H2 H3
H4.
8. ALTERNATE METHOD OF COMPUTATION
The
above assumes that the sequence W0, ... ,
W79 is implemented as an array of eighty
32-bit words. This is efficient from the standpoint of minimization of
execution time, since the addresses of Wt-3, ... ,Wt-16 in step
(b) are easily computed. If space is at a premium, an alternative is to
regard { Wt } as a circular queue, which
may be implemented using an array of sixteen 32-bit words W[0], ... W[15].
In this case, in hex let MASK = 0000000F. Then processing of Mi is as follows:
- a. Divide Mi into 16 words W[0], ...
, W[15], where W[0] is the left-most word.
- b. Let A = H0, B = H1, C = H2, D =
H3, E = H4.
- c. For t = 0 to 79 do
- s = t ^ MASK;
- if (t >= 16) W[s] = S1(W[(s +
13) ^ MASK] XOR W[(s + 8) AND MASK] XOR W[(s + 2) ^ MASK] XOR W[s]);
- TEMP = S5(A) + ft(B,C,D) + E + W[s] + Kt;
- E = D; D = C; C = S30(B); B = A; A
= TEMP;
- d. Let H0 = H0 + A, H1 =
H1 + B, H2
= H2 + C, H3 = H3 + D,
H4 = H4 +
E.
9. COMPARISON OF METHODS
The methods of
Sections 7 and 8 yield the same message digest. Although using the method
of Section 8 saves sixty-four 32-bit words of storage, it is likely to
lengthen execution time due to the increased complexity of the address
computations for the { W[t] } in step (c). Other computation methods which
give identical results may be implemented in conformance with the
standard.

