CIS 9615. Analysis of Algorithms

Amortized Analysis

 

Amortized analysis considers the averages time expense of a group of operations in the worst-case.

It is different from the average expense of all instances.

1. Aggregate analysis

If n operations cost T(n) time in total, then each of them has an amortized cost of T(n)/n.

Example: For a stack S containing n objects, operations PUCH(S, x) and POP(S) take O(1) time, and MULTIPOP(S, k) takes O(n) time, while the amortized cost of the three is O(1), since each object can be popped at most once for each time it is pushed.

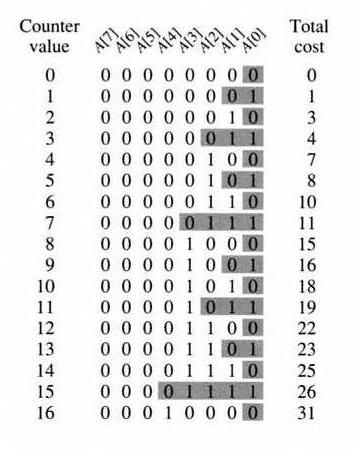
Example: For a k-bit binary counter, the worst case cost of an INCREMENT operation is Θ(k). However, the time taken by n INCREMENT operations is not Θ(nk), but n + n/2 + n/4 + ... < 2n. Therefore the amortized cost of INCREMENT is Θ(1).
08-01 (28K)

2. The accounting/potential method

If certain objects give credit as the difference between the amortized cost and actual cost of certain operation, certain later operation can be paid by the credit.

Example: For a stack containing n objects, let PUSH have amortized cost 2, and POP and MULTIPOP have amortized cost 0. Therefore, each actual PUSH operation generates 1 credit on the object, which can be spent by the following POP and MULTIPOP. Again, the amortized cost of the three is O(1).

Example: For a k-bit binary counter, let a change from 0 to 1 have amortized cost 2, and 1 to 0 have amortized cost 0. Since the actual cost of changing 0 to 1 is 1, a credit is produced by such an operation on the bit for the other operation to spend. Again, the amortized cost of INCREMENT is Θ(1).

The potential method is similar to the accounting method, except it uses a "potential" defined on the whole data stucture, rather than "credits" on individual data objects.

Example: For a stack containing n objects, define the potential to be n.

Example: For a binary counter, define the potential as the number of 1s in it.

 

3. Dynamic tables

In a dynamic table, object insertion/delection at the end of the table may trigger table expansion/contraction for the allocating/releasing of memory.

08-02 (57K)

The cost of the algorithm:

08-03 (24K)

Therefore, the amortized cost of the algorithm is about 3 (assignments), a constant.

The same conclusion can be obtained by the accounting method or the potential method.

If the deletion algorithm triggers a table contraction, it can be analyzed similarly.

When both table expansion and contraction are allowed, it is better to set different load-factor thresholds to trigger them, to avoid frequent expansion-contraction cycle.

Assume expansion happens when the table is 1/2 full, and contraction happens when the table is 1/4 full, the amortized cost of insertion and deletion is O(1). [Proof]