
Greedy Algorithms
Compared with dynamic programming: faster, though may miss the optimal solution.
A problem exhibits optimal substructure if an optimal solution to the problem contains optimal solutions to the sub-problems. Roughly speaking, a greedy algorithm is optimal if its greedy choices are included in optimal choices (details).
Dynamic programming solution: consider Sij, the set of all activities compatible with ai and aj where fi < sj, then finally decide the size of the maximum compatible subset of S0,n+1. For each Sij, the size of the maximum compatible subset can be obtained by going through all ak in the set, so to recursively reduce the problem to Sik and Skj.
Greedy solution: recursively find the activity that is compatible with the current schedule while having the earliest finish time, and add it into the schedule.
The solution can be proved to be optimal: the earliest-finished activity must be in the optimal solution.
A recursive algorithm initially called as Recursively-Activity-Selector(s, f, 0, n+1), with the activities sorted by finish time.

A more efficient iterative algorithm:
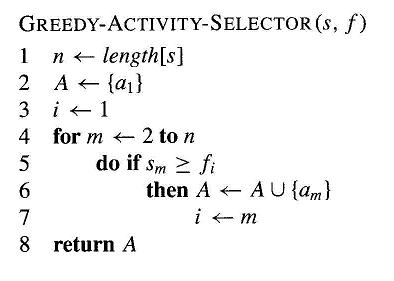
What are the growth orders of these algorithms?
Assuming binary prefix coding, a solution can be represented by a binary tree, with each leaf corresponds to a unit, and its path from root represents the code for the unit. An optimal code is a full binary tree with the minimum expected path length.
In the following algorithm, C contains a set of symbols, and f contains the frequency values of the units. Q is a priority queue, implemented by a heap.

Example:
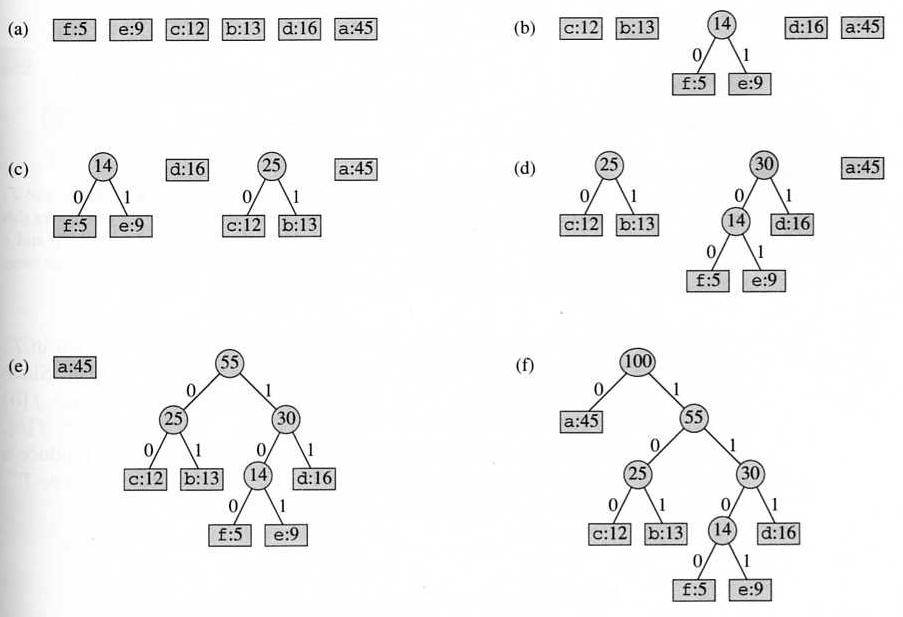
The running time of the algorithm is O(n lg n): n elements in a min-heap.
The average code length equals to the sum of all the probability values in the internal nodes of the tree.
Compared to optimal binary search tree: similarity and difference.
Best-First Search: if the next step is selected at the neighborhood of all explored points, "hill climbing" become "best-first search".