Linear Structures and Hash Tables
A dynamic set S usually supports the following "dictionary operations":
When implemented, a data structure represents the relation/order among objects in a domain as relation/order among data items in a computer. Different data structures handle the above operations differently.
There are two basic ways to represent a relation in computer:
For a linear data structure, the order among elements is implicitly represented in an array, and explicitly in a linked list. Between the two, an array is more efficient in access at any position ("random access"), while a linked list is more efficient in insertions and deletions at a given position.
A linked list can also be implemented by two arrays, one of which keeps the elements themselves, and the other keeps the index of the successor for each element. Similarly, multiple arrays can be used to represent an array of objects with multiple fields by using the same index to tie the fields together.
In an Object-Oriented Programming language, linked lists are often implemented in two ways, with or without a specific "head" object containing the reference to the first node. Without such a head, the "node" class and the "list" class are merged, and the list is defined recursively as either empty or a node succeeded by a list.
To move in both directions in a linked list, an additional link can be used to turn a singly-linked list into a doubly-linked list.

The following are some common list operations, where L is a list, k is a key, x is a node to be inserted after node y in a list.
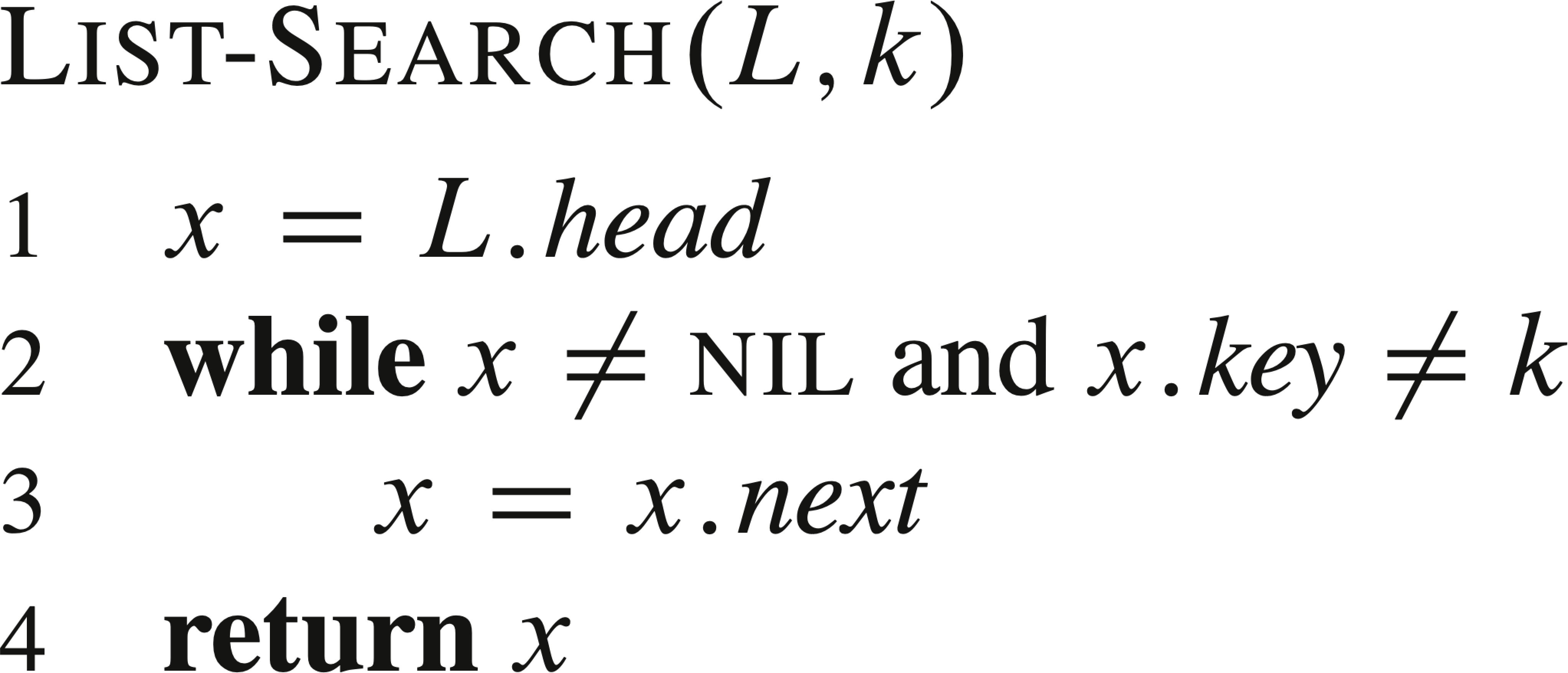
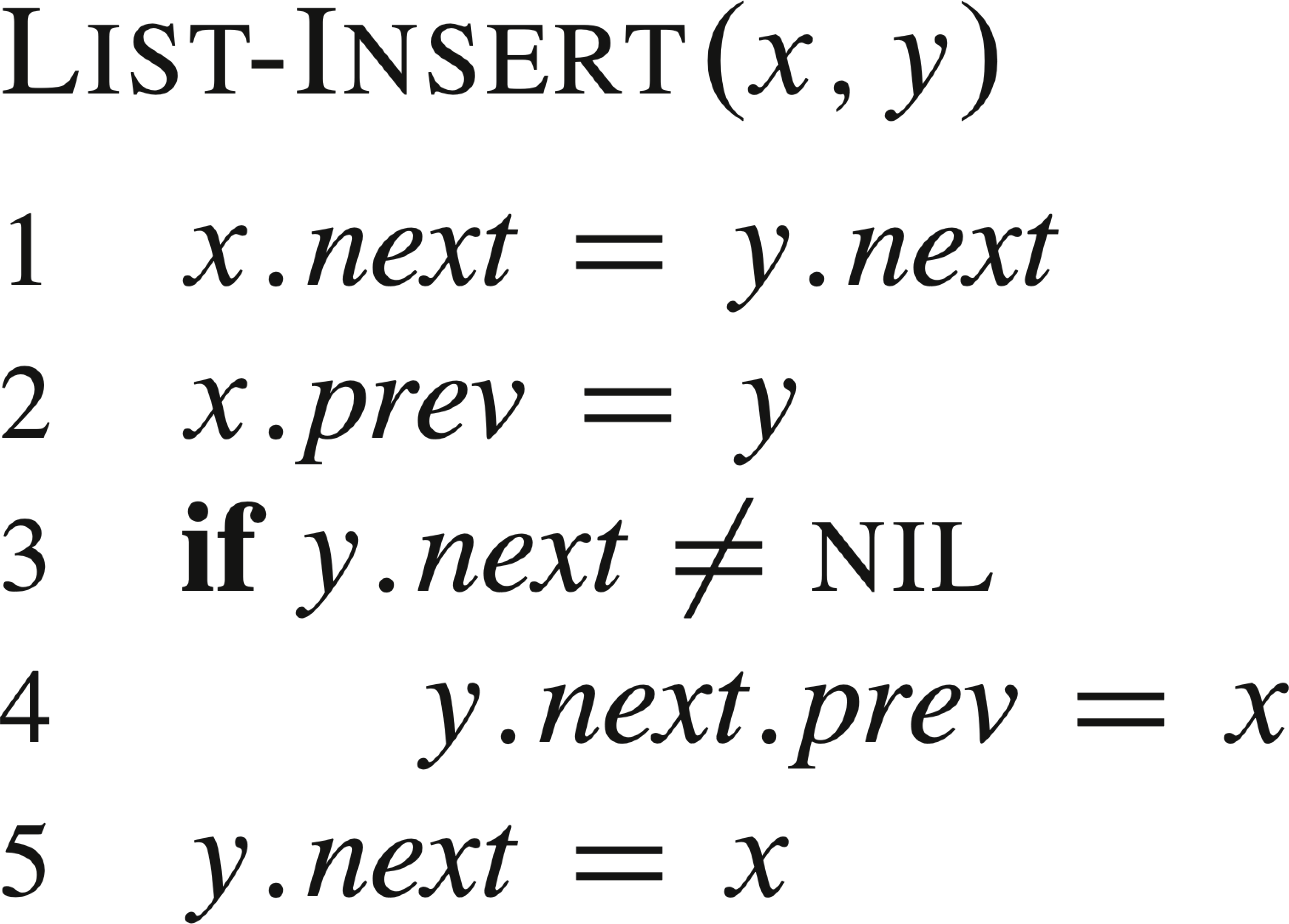

A L.tail can be added to directly access the last element. If the first and the last nodes points to each other, the link becomes circular.
To turn an array of length n into a circular array, use index = (index mod n) + 1. In a linked list, let the last element point to the first element.
Insert/Delete on stack and queue are taken as Θ(1) operations, and the size of the data structure automatically grows when needed.
Both stack and queue can be implemented by array and linked list:
| STACK | QUEUE | |
| array | operations happen at the highest index value | a circular array is needed to work on both ends |
| linked list | a reference points to the last node | two references points to both end, and in a singly-linked list, deletion can only happen at one end |
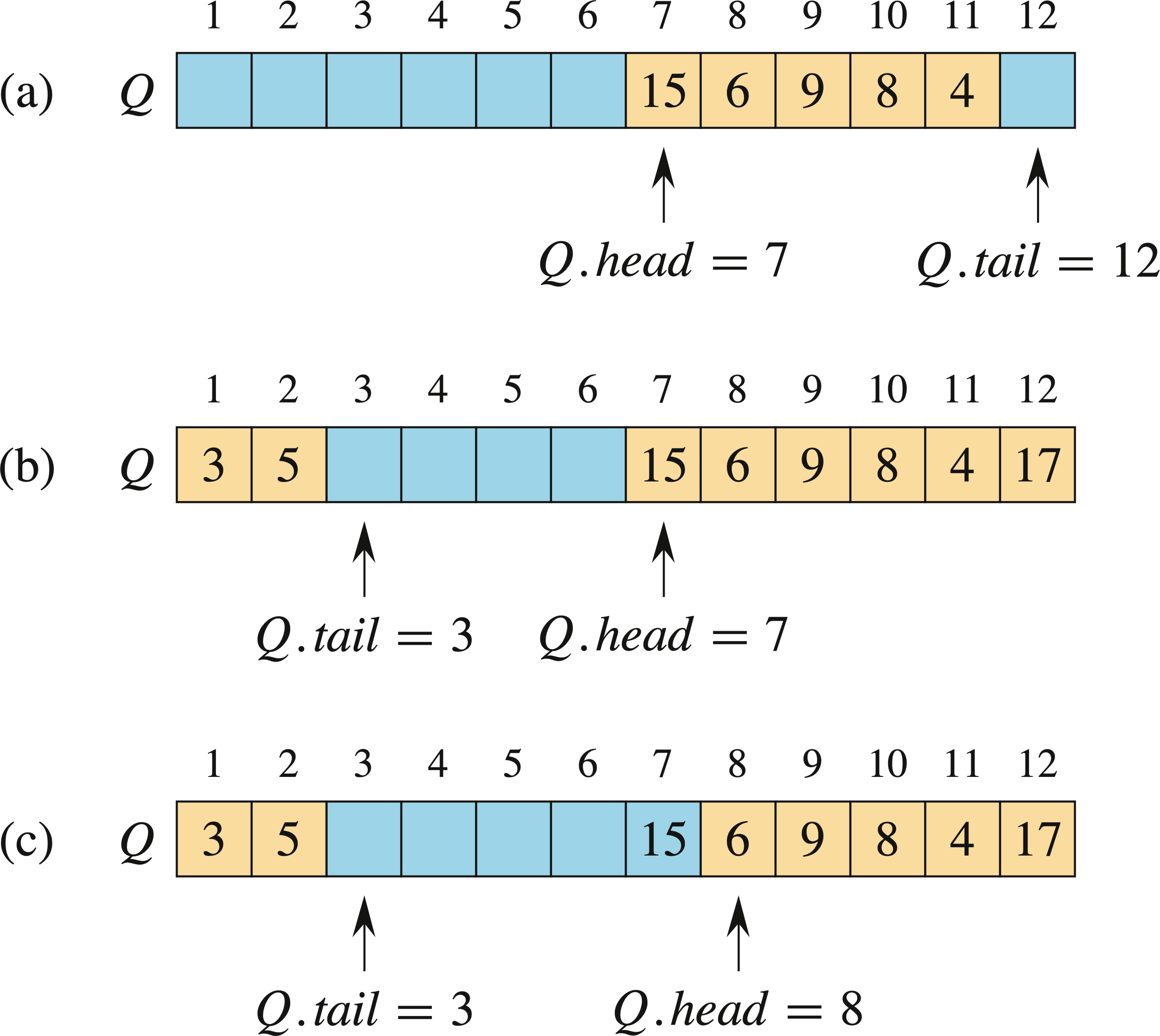
 Array-Queue:
Array-Queue:
Among the three operations, each insertion and deletion usually requires a search (as duplicate keys are not allowed), therefore search is the representative operation in efficiency analysis. Since search is normally a mapping from a key to an index in the table, the intuition behind hash table is to directly build such a mapping index = h(key), without comparing the key with the elements in the table. Since the range of index is much smaller than the range of key, the mapping is many-to-one, not one-to-one.
The design of a hash table consists of two major decisions: (1) to define a hash function index = h(key), (2) to handle "collisions", the situation where multiple keys are mapped into the same index.
Typically, the size of a hash table is proportional to the number of keys actually stored, while being much smaller than the range of possible keys.
A good hash function should distribute the keys evenly in the table. Often, a hash function works in two steps: (1) to convert a key into an integer, (2) to calculate the index from the integer. Therefore, hash function discussion often assumes that the function is a mapping from an integer (key) to an integer (index).
The most common hash function is to take the reminder of the key divided by the size of the hash table, that is, h(k) = k mod m, assuming index in [0, m − 1]. A more complicated version is h(k) = f(k) mod m, where f(k) does additional calculation to reduce collision, and the reminder operation makes the function value to cover the whole table. If it is easier to turn the keys into real numbers, the hash function can be h(k) = floor(g(k) * m), where g(k) maps k into the range of [0, 1).
Common collision handling methods can be divided into two types, open addressing, where all elements are stored in the table itself, and separate chaining, where elements are stored outside the table in (sorted) linked-lists ("buckets"). Separate chaining requires additional space, though is conceptually simpler than open addressing.
 In open addressing, the hash function generates a probe sequence to tell the element where to go if the slot indicated by the hash function is already occupied by a different key. Such a sequence can depend on the key (such as double hashing) or follow a fixed pattern (such as linear probing and quadratic probing). In either way, element comparisons are necessary, as collision can happen in multiple places. After deletion, the released space is often marked for the following search to pass through. Since insertion includes search, a new key can be stored in a previously occupied space only after the searching stops at a never-occupied space somewhere down the path. Another strategy is lazy deletion that relocates some element in a following search. To make things simple, we can also only insert into an empty cell, and let the "previous-occupied" marks be cleared periodically by re-hashing all elements.
In open addressing, the hash function generates a probe sequence to tell the element where to go if the slot indicated by the hash function is already occupied by a different key. Such a sequence can depend on the key (such as double hashing) or follow a fixed pattern (such as linear probing and quadratic probing). In either way, element comparisons are necessary, as collision can happen in multiple places. After deletion, the released space is often marked for the following search to pass through. Since insertion includes search, a new key can be stored in a previously occupied space only after the searching stops at a never-occupied space somewhere down the path. Another strategy is lazy deletion that relocates some element in a following search. To make things simple, we can also only insert into an empty cell, and let the "previous-occupied" marks be cleared periodically by re-hashing all elements.
Elastic hashing and Funnel Hashing is a new approach that divides a hashtable into sub-tables to improve the expected search cost in open addressing.
In general, the average cost of the major operations of a hash table is considered Θ(1), though the worst-case cost is Θ(n).