CIS 5511. Programming Techniques
Growth of Functions
A central topic in algorithm analysis is to compare the time complexity (or efficiency) of algorithms (for the same problem).
As the running time of an algorithm is represented as T(n), a function of instance size, the problem is transformed into the categorization of these functions.
1. Asymptotic notations
To simplify the analysis of the time expense of algorithms, the following assumptions are usually made:
- A size measurement can be established among the (infinite number of) instances of a problem to indicate their difficulty, so that the time spent by an algorithm on an instance is a nondecreasing function of its size (at least after a certain point);
- To compare the efficiency of algorithms on all problem instances, what matters is the instances larger than a certain size, as there are only finite smaller ones, but infinite larger ones since size has no upper bound;
- No matter where the threshold is set, in general the algorithm that grows faster will cost more than another one that grows slower, so what really matters is not T(n), but its derivative T'(n);
- Since it is impossible to compare the growth rates of all functions, it is often enough to categorize them by order of growth, with a simple function to identify each category.
The asymptotic efficiency of an algorithm is studied, that is, how its running time increases with the size of input in the limit, roughly speaking.
- Θ(g(n)) = {f(n) : There exist positive constants c1, c2, and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0}. We say that g(n) is an asymptotically tight bound of f(n), and write f(n) = Θ(g(n)). [It actually means f(n) ∈ Θ(g(n)). The same for the following.]
- O(g(n)) = {f(n) : There exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0}. We say that g(n) is an asymptotically upper bound of f(n), and write f(n) = O(g(n)).
- Ω(g(n)) = {f(n) : There exist positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0}. We say that g(n) is an asymptotically lower bound of f(n), and write f(n) = Ω(g(n)).
- o(g(n)) = {f(n) : For any positive constant c > 0, there exist a constant n0 > 0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0}. We say that g(n) is an upper bound of f(n) but not asymptotically tight, and write f(n) = o(g(n)).
- ω(g(n)) = {f(n) : For any positive constant c > 0, there exist a constant n0 > 0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0}. We say that g(n) is a lower bound of f(n) but not asymptotically tight, and write f(n) = ω(g(n)).
 Examples:
Examples:
- 4n3 − 10.5n2 + 7n + 103 = Θ(n3)
- 4n3 − 10.5n2 + 7n + 103 = O(n3)
- 4n3 − 10.5n2 + 7n + 103 = Ω(n3)
- 4n3 − 10.5n2 + 7n + 103 = O(n4)
- 4n3 − 10.5n2 + 7n + 103 = Ω(n2)
- 4n3 − 10.5n2 + 7n + 103 = o(n4)
- 4n3 − 10.5n2 + 7n + 103 = ω(n2)
Intuitively, the five notations correspond to relations =, ≤, ≥, <, and >, respectively, when applied to compare growth order of two functions (though not all functions are asymptotically comparable). All of the five are transitive, the first three are reflexive, and only the first one is symmetric.
Relations among the five:
- f(n) = Θ(g(n)) if and only if f(n) = O(g(n)) and f(n) = Ω(g(n)).
- f(n) = O(g(n)) if and only if f(n) = Θ(g(n)) or f(n) = o(g(n)).
- f(n) = Ω(g(n)) if and only if f(n) = Θ(g(n)) or f(n) = ω(g(n)).
- f(n) = O(g(n)) if and only if g(n) = Ω(f(n)).
- f(n) = o(g(n)) if and only if g(n) = ω(f(n)).
One way to distinguish them:
- f(n) = Θ(g(n)) if and only if Lim[f(n)/g(n)] = c (a positive constant).
- f(n) = o(g(n)) if and only if Lim[f(n)/g(n)] = 0.
- f(n) = ω(g(n)) if and only if Lim[f(n)/g(n)] = ∞.
The common growth orders, from low to high, are:
- constant: Θ(1)
- logarithmic: Θ(logan), a > 1
- polynomial: Θ(na), a > 0
- exponential: Θ(an), a > 1
- factorial: Θ(n!)
Polynomial functions can be further divided into linear (Θ(n)), quadratic (Θ(n2)), cubic (Θ(n3)), and so on.
Asymptotic notions can be used in equations and inequalities, as well as in certain calculations. For example,
2n2 + 3n + 1 = Θ(n2) + Θ(n) + Θ(1) = Θ(n2).
In algorithm analysis, the most common conclusions are worst-case expenses expressed as O(g(n)), which can be obtained by focusing on the most expensive step in the algorithm, as in the analysis of Insertion Sort algorithm.
2. Analysis of recurrences
When an algorithm contains a recursive call to itself, its running time can often be described by a recurrence, i.e., an equation or inequality that describes a function in terms of its value on smaller inputs.
A "divide-and-conquer" approach often uses D(n) time to divide a problem into a number a of smaller subproblems of the same type, each with 1/b of the original size. After the subproblems are solved, their solutions are combined in C(n) time to get the solution for the original problem. This process is repeated on the subproblems, until the input size becomes so small (less than a constant c) that the problem can be solved directly (usually in constant time) without recursion. This approach gives us the following recurrence:
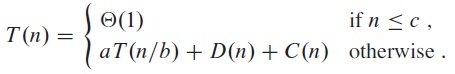 For example, for the Merge Sort algorithm, we have
For example, for the Merge Sort algorithm, we have
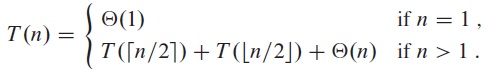
This is the case, because each time an array of size n is divided into two halves, and to merge the results together takes linear time.
Often we need to solve the recurrence, so as to get a running time function without recursive call.
One way to solve a recurrence is to use the substitution method, which uses mathematical induction to prove a function that was guessed previously.
For example, if the function is
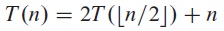
one reasonable guess is T(n) = O(n lg n). To show that this is indeed the case, we can prove that T(n) ≤ c n lg n for an appropriate choice of the constant c > 0. We start by assuming that this bound holds for halves of the array, then, substituting into the recurrence yields,
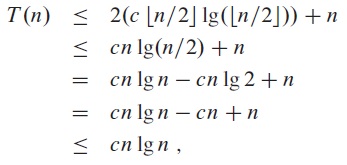
where the last step holds as long as c ≥ 1.
Furthermore, mathematical induction requires us to show that the solution holds for the boundary cases, that is, we can choose the constant c large enough so that T(n) ≤ c n lg n holds there. For this example, if the boundary condition is T(1) = 1, then c = 1 does not work there because c n lg(n) = 1 1 lg(1) = 0. To resolve this issue we only need to show that for n = 2, we do have T(n) ≤ c 2 lg 2 as long as c ≥ 2.
In summary, we can use c ≥ 2, and we have shown that T(n) ≤ c n lg n for all n ≥ 2.
To get a good guess for recurrence function, one way is to draw a recursion tree. For example, if the function is
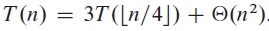
we can create the following recursion tree:
To determine the height of the tree i, we have n / 4i = 1, that is, i = log4n. So the tree has log4n + 1 levels.
At level i, there are 3i nodes, each with a cost c(n / 4i)2, so the total is (3/16)icn2.
At the leaves level, the number of nodes is 3log4n, which is equal to nlog43 (because alogbc = clogba). At that level, each node costs T(1), so the total is nlog43T(1), which is Θ(nlog43).
After some calculation (see Section 4.4 of the textbook for details), the guess T(n) = O(n2) can be obtained.
Finally, there is a "master method" that provides a general solution for divide-and-conquer recurrence. Intuitively, the theorem says that the solution to the recurrence is determined by comparing the costs at the top and bottom levels of the recursion tree:
 The above example falls into Case 3.
The proof of the master theorem is given in the textbook. It is important to realize that the three cases of the master theorem do not cover all the possibilities.
As a special case, when a = b we have logba = 1. The above results are simplified to (1) Θ(n), (2) Θ(n lg n), and (3) Θ(f(n)), respectively, depending on whether f(n) is linear, or faster/slower than linear. We can see that Merge Sort belongs to Case 2.
The above example falls into Case 3.
The proof of the master theorem is given in the textbook. It is important to realize that the three cases of the master theorem do not cover all the possibilities.
As a special case, when a = b we have logba = 1. The above results are simplified to (1) Θ(n), (2) Θ(n lg n), and (3) Θ(f(n)), respectively, depending on whether f(n) is linear, or faster/slower than linear. We can see that Merge Sort belongs to Case 2.

 Examples:
Examples:
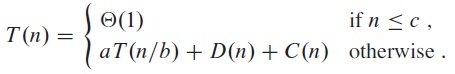 For example, for the Merge Sort algorithm, we have
For example, for the Merge Sort algorithm, we have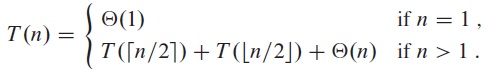
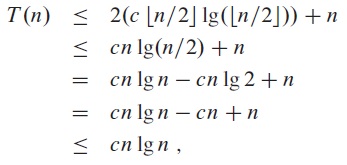

 The above example falls into Case 3.
The proof of the master theorem is given in the textbook. It is important to realize that the three cases of the master theorem do not cover all the possibilities.
As a special case, when a = b we have logba = 1. The above results are simplified to (1) Θ(n), (2) Θ(n lg n), and (3) Θ(f(n)), respectively, depending on whether f(n) is linear, or faster/slower than linear. We can see that Merge Sort belongs to Case 2.
The above example falls into Case 3.
The proof of the master theorem is given in the textbook. It is important to realize that the three cases of the master theorem do not cover all the possibilities.
As a special case, when a = b we have logba = 1. The above results are simplified to (1) Θ(n), (2) Θ(n lg n), and (3) Θ(f(n)), respectively, depending on whether f(n) is linear, or faster/slower than linear. We can see that Merge Sort belongs to Case 2.