Heuristic Search
The other extreme is "completely-informed search", where at each node the best option is known. Actually in such a case no "search" is really needed, since the path from the initial state to the final state is known.
Both above cases can be handled well in computer science. AI is interested in the situation in the middle: the intermediate nodes do have information on how promising each option is, though the information is not always accurate and certain.
A "heuristic function" is a function used to rank the alternatives in each step according to available information. Such a function is usually based on experience and intuition about the given problem.
Heuristic search is similar to depth-first search and breadth-first search, except that its "open-node list" is a priority queue, in which the nodes are sorted by a heuristic function. Consequently in every step the algorithm explores the current-best direction, therefore it is also called "best-first search". The actual efficiency of such an algorithm is determined by the quality of the heuristic function.
Beside looking for a path to a goal state, search can also be used to solve optimization problems, where each state has an evaluation value attached, and the problem is to find the state with the highest value. In this situation, local (i.e., without memory) best-first search is also called "hill climbing". Such a procedure stops at local maxima.
A well-known example is the General Problem Solver, which uses Means-Ends Analysis to get a heuristic function.
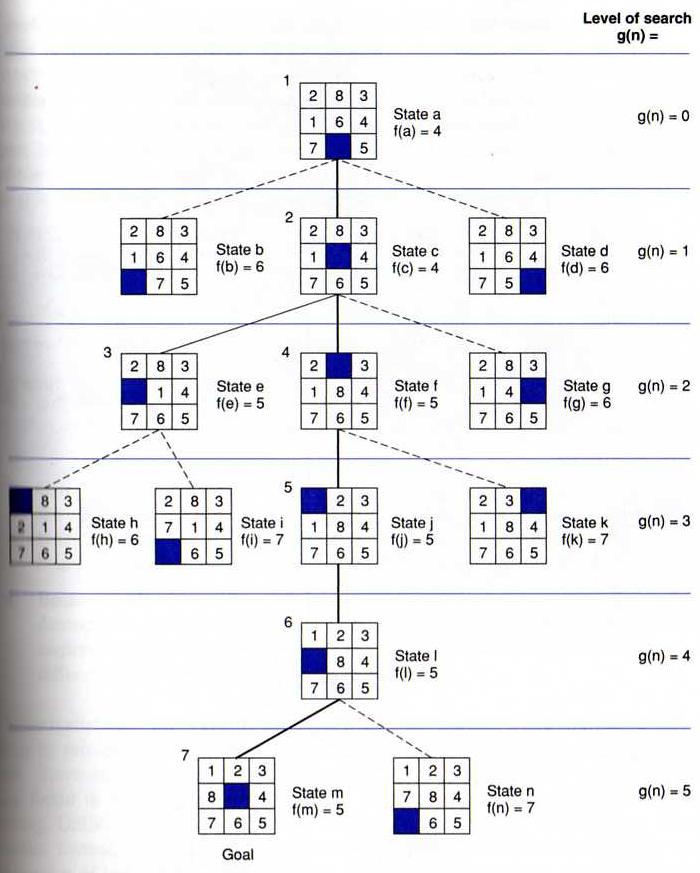
A* algorithm is a typical heuristic search algorithm, in which the heuristic function is an estimated shortest distance from the initial state to the closest goal state, and it equals to the traveled distance plus the predicted distance ahead. That is, f(n) = g(n) + h(n).

Other sample Prolog implementations of best-first search: Program 1, Program 2.