State Space Search
If each state is represented by a node, and each possible change is represented by a link, then a "problem" can be represented as a graph (the "state space"), with a "solution" corresponding to a path from the initial state to a final state.
In this way, a solution consists of a sequence of operations, each of which changes one state into another one, and the whole sequence changes the initial state into a final state in multiple steps.
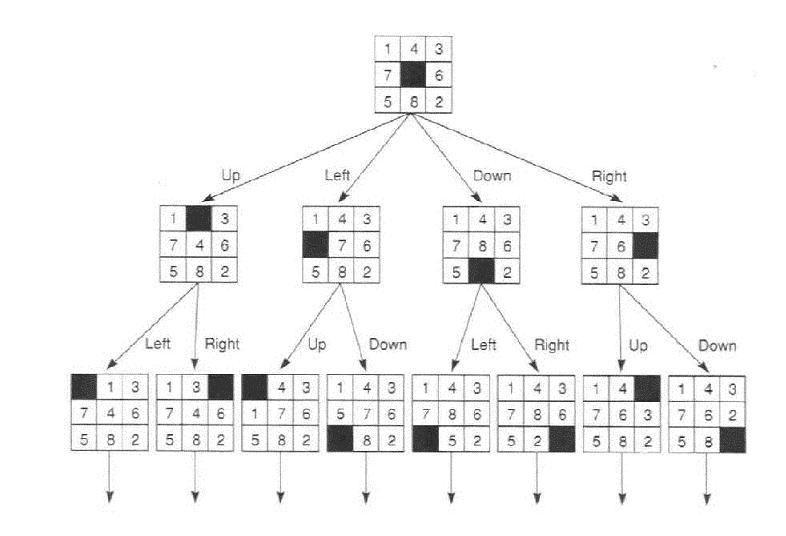
Example: 8-puzzle.
Initial state:
Goal state:
Partial state space:

Tower of Hanoi is another example.
The search strategy should be correct, complete, and efficient. Sometimes we also want it to be able to find the optimal solution (such as the shortest path).
Even though a solution is a path that, by definition, starts at the initial state and ends at a final state, sometimes it is better to start the search from the goal (say, the only final state), and to go backwards. More complicated methods combine the two (forward and backward, or data-driven and goal-driven) search directions.
After the starting node is decided, there are two common ways to systematically search a graph without additional information (i.e., beside the nodes and links): depth-first and breadth-first. Both algorithms remembers the nodes that have been visited so far, and separate them into an "open" group (for nodes with unvisited neighbor) and a "closed" group (for nodes without unvisited neighbor). Their difference is: depth-first search uses a stack to keep the "open" group, so it tries to go as far away from the starting node as possible; breadth-first search uses a queue to keep the "open" group, so it tries to stay as close to the starting node as possible.
In depth-first search, if it is possible to move on both directions in a link, search can be done without the stack. The program can start at the root, then go all the way done, then back up, i.e. "backtrack" to the previous node to try another possibility.
A variation of depth-first search is called depth-first search with iterative deepening. The algorithm repeatedly does depth-first search with a depth bound, which is then increased if the current iteration fails to find a solution.
Generally speaking, different search strategies may work better on different problems.
path(Z, Z). path(X, Y) :- move(X, W), not(been(W)), assert(been(W)), path(W, Y). move(a, b). move(b, a). move(a, c). move(c, d). move(a, e). move(d, f).We can have the following sample run:
?- assert(been(a)), path(a,f). true. ?- listing(been). :- dynamic been/1. been(a). been(b). been(c). been(d). been(f). ?- retractall(been(_)). true. ?- assert(been(a)), path(a, X). X = a ; X = b ; X = c ; X = d ; X = f ; X = e ; false. ?- assert(been(a)), path(a, X). X = a ; false.The assert(been(a)) is used to prevent SWI-Prolog from complaining "undefined predicate" when not(been(W)) is called before any been fact is inserted.
From the result of trace, we can see that the search is depth-first.
The last call path(a, X) only gives one answer, because all the "been" facts inserted during the previous run are still in the database. To remove them, use retractall(been(_)).
Another program (path/3) that does not use "global variables" but a "local variable" to keep the visited node list is given here:
path(Z, Z, _). path(X, Y, L) :- move(X, W), not(member(W, L)), path(W, Y, [W|L]).Try it as the following:
?- path(a, X, [a]).and ask for all the answers. The result should be the same as above. If the goal is repeated, the result will be repeated, too, because this program does not change the database.
The on-line tutorial has code for Graph structures and paths and Search.