3203. Introduction to Artificial Intelligence

Learning: Symbolic Approaches

 

1. Introduction

Learning is an important aspect of intelligence, and a promising solution to many AI problems. It has been a central issue in the field from the very beginning — Alan Turing (1950) suggested that the most likely way to get a "thinking machine" is to build a "child machine" first, then to "educate" it. Many ideas have been proposed, often under the name of "machine learning". In the following only some representative approaches are briefly introduced.

Roughly speaking, learning is the ability of an agent to improve its behavior based on experience. There are two critical aspects in such a definition:

We will revisit these issues while describing various approaches of learning.

 

2. Concept learning

One type of concept learning is to learn a concept from given examples, which can be positive or negative. Since the examples are already classified, this is a form of supervised learning.

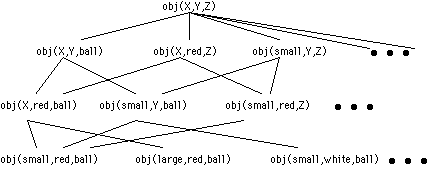
One approach is to gradually refining the hypothesis space. If all hypothesis are Boolean expressions, then the version space contains the hypothesis that are consistent with the examples. The learning is carried out by a candidate-elimination algorithm. In this process, a positive example specifies what a concept should include, and a negative example specifies what it should not include. They can be used to eliminate candidates that are either too general or too specific, so as to reduce the version space.

A Prolog implementation of this algorithm is here that works on the following hypothesis space, where each object is specified by size, color, and shape.

If the examples are described by their attribute values, but not classified, concepts can be learned via unsupervised learning or clustering by recursively merge or split the current class(es), with the hope to achieve the minimum intra-class distances and the maximum inter-class distances.

When the system needs to distinguish the instances of multiple given concepts, the procedure is sometimes represented as a "decision tree": given an object or a situation specified by a set of attributes, the tree decides which concept it belongs to. Each internal node in the tree represents a test on one of those attributes, and the branches from the node are labeled with the possible outcomes of the test. Each leaf node is a Boolean classifier for the input instance. It is similar to the "20 Questions" game.

To learn an efficient decision tree: to recursively split the class into subclasses using a property, until all subclasses contains examples of the same categorization. When there are multiple ways to split a class, try to do so as evenly as possible.

 

3. Inferential learning

Non-deductive inference (such as induction, Abduction, and analogy) are often considered as learning, because their conclusion usually contains information beyond that in the premises. Various types of approaches have been explored in AI.

Ryszard S. Michalski proposed an inferential theory of learning, in which various types non-deductive inference, like induction and analogy, are formalized in the framework of predicate logic, as ways to generate useful hypotheses.

Using inductive logic programming, general relationships (like the "rules" in Prolog) can be derived from concrete examples (like the "facts" in Prolog). The approach is similar to that of supervised concept learning (a tutorial). At the current time, this technique only produces relatively simple programs.

The approach taken in NARS is based on the assumption that quantitative measurement of evidential support is necessary in inferential learning. The working examples can help to explain how the system works.

 

4. Genetic programming

While most learning approaches make changes according to available evidence, genetic programming learns by making random changes, then selectively keeping the good ones.

Closely related to genetic algorithm, in genetic programming a program (typically in a functional programming language, such as Lisp) is represented as a binary tree.

Genetic programming takes four steps to solve problems:

  1. Generate an initial population of random compositions of the functions and terminals of the problem.
  2. Execute each program in the population and assign it a fitness value according to how well it solves the problem.
  3. Create a new population of computer programs by copy, crossover, and mutation, according to fitness values of the programs.
  4. The best computer program that appeared in any generation, the best-so-far solution, is designated as the result.