1. Introduction

The most common used AI technique in game is search. In some other problem-solving activities, state change is solely caused by the action of the system itself. However, in multi-player games, states also depend on the actions of other players (systems) who usually have different goals.

A special situation that has been studied most is two-person zero-sum game, where the two players have exactly opposite goals, that is, each state can be evaluated by a score from one player's viewpoint, and the other's viewpoint is exactly the opposite. This type of game is common, and easy to analyze, though not all competitions are zero-sum!

There are perfect information games (such as Chess and Go) and imperfect information games (such as Bridge and games where dice are used). Given sufficient time and space, usually an optimum solution can be obtained for the former by exhaustive search, though not for the latter. However, for most interesting games, such a solution is usually too inefficient to be practically used.

2. Minimax Procedure

First, we distinguish two types of nodes, MAX and MIN, in the state graph, determined by the depth of the search tree.

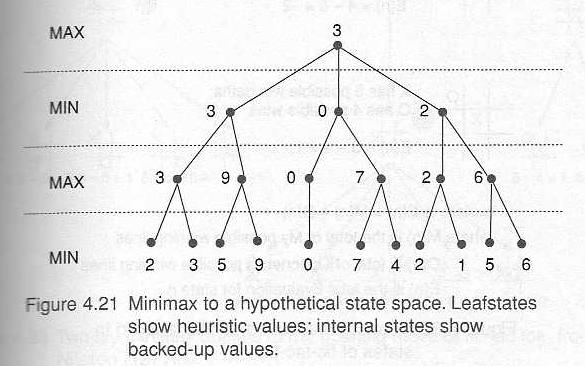
Minimax procedure: starting from the leaves of the tree (with final scores with respect to one player, MAX), and go backwards towards the root (the starting state).

At each step, one player (MAX) takes the action that leads to the highest score, while the other player (MIN) takes the action that leads to the lowest score.

All nodes in the tree will all be scored, and the path from root to the actual result is the one on which all nodes have the same score.

Example:

Because of computational resources limitation, the search depth is usually restricted, and estimated scores generated by a heuristic function are used in place of the actual score in the above procedure.

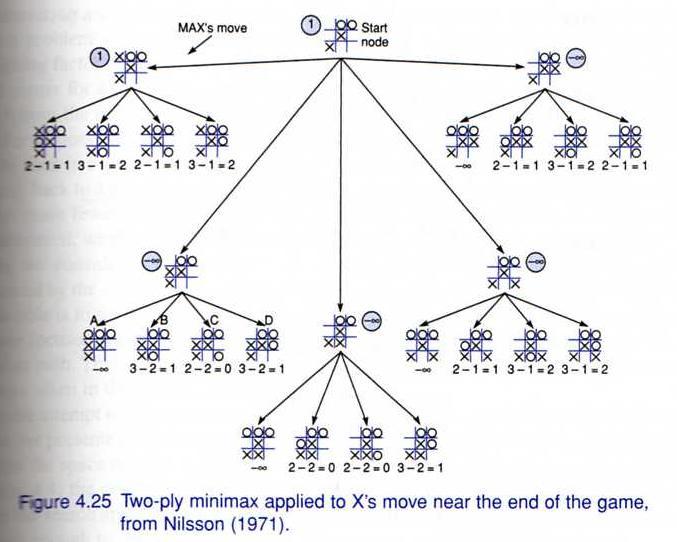
Example: Tic-tac-toe, with the difference of possible win paths as the henristic function.

3. Alpha-Beta Pruning

Based on explored nodes' score, inequity can be set up for nodes whose children haven't been exhaustively explored. Under certain conditions, some branches of the tree can be ignored without changing the final score of the root.

In Alpha-Beta Pruning, each MAX node has an alpha value, which never decreases; each MIN node has a beta value, which never increases. These values are set and updated when the value of a child is obtained. Search is depth-first, and stops at any MIN node whose beta value is smaller than or equal to the alpha value of its parent, as well as at any MAX node whose alpha value is greater than or equal to the beta value of its parent.

Examples: in the following partial trees, the other children of node (5) do not need to be generated.

 (1)MAX[>=3] ----- (2)MIN[==3] ----- (3)MAX[==5] 
     |                 |------------ (4)MAX[==3]
     |
     |------------ (5)MIN[<=0] ----- (6)MAX[==0]
                       |-----------X
                       |-----------X


 (1)MIN[<=5] ----- (2)MAX[==5] ----- (3)MIN[==5] 
     |                 |------------ (4)MIN[==3]
     |
     |------------ (5)MAX[>=8] ----- (6)MIN[==8]
                       |-----------X
                       |-----------X

4. Sample Games

• Some games have been solved, so a computer can play perfectly.
• IBM's Deep Blue won a Chess match against a world champion, though it is not perfect.
• The game Go (online demo) has a huge state space, so humans are still better.