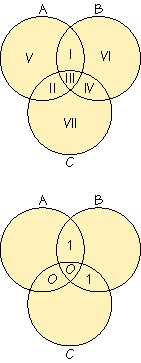
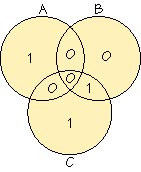
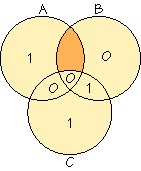
c1 = a1+a2+a3, c2 = a1+a3+a4, c3 = a2+a3+a4

1: message, 2: code word, 3: received code, 4: error correction
Error detection with parity-check sums: adding an extra bit to keep an even parity (or odd parity).
How error-correcting code works: (1) divide bits in code into (overlapping) groups, (2) decide the parity of every group, (3) confirm parity during encoding and decoding.
Example: When the message is a1a2a3a4, the code word is a1a2a3a4c1c2c3, where
c1 = a1+a2+a3, c2 = a1+a3+a4, c3 = a2+a3+a4




1: message, 2: code word, 3: received code, 4: error correction

The weight of a binary code is the minimum number of 1's that occur among all nonzero code words of that code.
Assume the weight of a binary code is t. The code will detect (though not fix) t-1 errors. If t is odd, the code will correct (t-1)/2 errors, if t is even, the code will correct (t-2)/2 errors. For example, the weight of the above code (Table 17.1, page 534) is 3, so it can either detect 2 errors or correct 1 error.
The distance between two binary strings of equal length is the number of positions in which the two strings differ.
Nearest-Neighbor Decoding Method
Another distance-based explanation of error correcting code.
Modular Arithmetic: m mod n is the remainder when m is divided by n.
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Credit card number, in binary code, can be encrypted and decrypted by adding the same binary key.
Homework: Chapter 17 Exercises No. 11, 21, 29, 32, 43