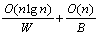 (1.1)
(1.1)
Analyzing a parallel algorithm means predicting the resources
that the algorithm requires, such as time, memory, disk space
and communication bandwidth. For most parallel programs time is
of the primary concern. Generally, by analyzing many candidate
algorithms for solving a given problem, a most efficient one can
often be identified. Such an analysis may indicate more than one
viable candidates, but several inferior ones are often discarded
in the process. In this paper we propose a methodology for analyzing
parallel programs. In particular, this method can assess the scalability
of sequential and parallel programs.
Analyzing the scalability of a algorithm means predicting its
potential elapsed times for varying input size, processor speed,
communication network and file system speeds. The results can
be useful in the design, implementation and maintenance of practical
applications.
We use a complexity-based method to capture the performance critical
parameters and their impact on the overall system elapsed time.
The sequential program's elapsed time is the basis of comparison.
Therefore scalability analysis requires models for both the sequential
and the parallel algorithms. We call these timing models.
Timing models capture the essential performance critical parameters
in one equation. Scalability analysis begins with a calibration
of the base points, i.e., uni-processor speed, file system and
network speeds. We then can scale up/down any parameters to conduct
what-if analysis.
This paper introduces techniques in building and using steady
state timing models via a set of diverse algorithms. Computational
results are used to validate the timing model predictions.
Keywords: Parallel programming, performance evaluation, scalability analysis, parallel program analysis.
Analyzing a parallel algorithm means predicting the resources
that the algorithm requires, such as time, memory, disk space
and communication bandwidth. For most parallel programs, we assume
time is of the primary concern. Generally, by analyzing many candidate
algorithms for solving a given problem, a most efficient one can
often be identified. Such an analysis may indicate more than one
viable candidates, but several inferior ones are often discarded
in the process.
Unlike conventional program complexity analysis, program scalability
analysis requires two specifications: a) characteristics of an
algorithm ; and b) characteristics of the processing environment.
For each program, a timing model should be established using these
specifications in order to generate estimated elapsed times. Scalability
analysis is to investigate the changes in elapsed times while
we alter algorithmic and processing specifications.
In this paper, since our main interests are in complexity analysis, we use the words algorithm and program interchangeably.
In sequential program scalability analysis, computing and input/output are the two major timing factors. For example, a typical sort program requires O(nlgn) computing steps and O(n) bytes for input/output when processing an input of size n. This gives a simple timing model as follows:
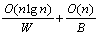 (1.1)
(1.1)
where W is the computing speed in "instructions
per second" and B is the file system's speed
in "bytes per second". We further assume that each input
consists of 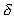 bytes and W
is a customized measure in "number of inputs per second".
This way the constant in the time complexity O(nlgn)
can be "hidden" in W. Thus, the new model
becomes:
bytes and W
is a customized measure in "number of inputs per second".
This way the constant in the time complexity O(nlgn)
can be "hidden" in W. Thus, the new model
becomes:
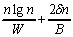 (1.2)
(1.2)
To begin scalability analysis, we need to establish the base points
of the program performance map by some computational experiments.
In this example, we first measure B by timing the
read and write blocks in the sort program that transfers 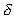 bytes 2n times. We then run the sort program to
obtain the total elapsed time (Tseq) sorting a problem
of size n. Finally, we derive a customized W
using B, n,
bytes 2n times. We then run the sort program to
obtain the total elapsed time (Tseq) sorting a problem
of size n. Finally, we derive a customized W
using B, n, 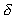 and (1.2).
These numbers establish the base point of the performance map
for the sort program.
and (1.2).
These numbers establish the base point of the performance map
for the sort program.
We then use (1.2) to examine the scalability of the sort program
by generating performance maps with varying W, B and n.
Table 1-3 illustrate the scalability analysis results for the
sort program.
| N | CPU(sec.) | I/O (sec.) | Time(sec.) |
| 10000 | 0.03 | 0.06 * | 0.09 * |
| 20000 | 0.05 | 0.13 | 0.18 |
| 40000 | 0.12 | 0.26 | 0.37 |
| 80000 | 0.25 | 0.51 | 0.76 |
| 160000 | 0.53 | 1.02 | 1.56 |
| 320000 | 1.13 | 2.05 | 3.17 |
| 640000 | 2.37 | 4.10 | 6.47 |
| 1280000 | 4.99 | 8.19 | 13.19 |
| 2560000 | 10.48 | 16.38 | 26.86 |
| 5120000 | 21.94 | 32.77 | 54.71 |
| 10240000 | 45.86 | 65.54 | 111.39 |
| 20480000 | 95.66 | 131.07 | 226.73 |
| 40960000 | 199.19 | 262.14 | 461.33 |
| 81920000 | 414.13 | 524.29 | 938.42 |
| 1.64E+08 | 859.77 | 1,048.58 | 1,908.35 |
* Calibrated points for B=2.5 MB/Sec. and W=5.2 MIPS
on a DEC Alpha/120 MHZ processor and NFS mount file system via
Ethernet.
Table 1. Sequential MergeSort Scalability by Input Size
| 10000 | 0.09 | 0.08 | 0.06 | 0.04 | 0.03 |
| 20000 | 0.18 | 0.16 | 0.12 | 0.09 | 0.07 |
| 40000 | 0.37 | 0.33 | 0.25 | 0.18 | 0.15 |
| 80000 | 0.76 | 0.68 | 0.51 | 0.38 | 0.31 |
| 160000 | 1.56 | 1.39 | 1.04 | 0.79 | 0.66 |
| 320000 | 3.17 | 2.83 | 2.15 | 1.64 | 1.38 |
| 640000 | 6.47 | 5.79 | 4.42 | 3.40 | 2.89 |
| 1280000 | 13.19 | 11.82 | 9.09 | 7.04 | 6.02 |
| 2560000 | 26.86 | 24.13 | 18.67 | 14.58 | 12.53 |
| 5120000 | 54.71 | 49.25 | 38.33 | 30.14 | 26.04 |
| 10240000 | 111.39 | 100.47 | 78.63 | 62.24 | 54.05 |
| 20480000 | 226.73 | 204.88 | 161.19 | 128.42 | 112.04 |
| 40960000 | 461.33 | 417.64 | 330.26 | 264.73 | 231.96 |
| 81920000 | 938.42 | 851.04 | 676.28 | 545.20 | 479.67 |
| 1.64E+08 | 1,908.35 | 1,733.59 | 1,384.06 | 1,121.92 | 990.84 |
Table 2. Scalability by Input Sizes and I/O Speeds (W=5.2MIPS)
| 10000 | 0.09 | 0.08 | 0.07 | 0.07 |
| 20000 | 0.18 | 0.16 | 0.14 | 0.13 |
| 40000 | 0.37 | 0.32 | 0.29 | 0.27 |
| 80000 | 0.76 | 0.64 | 0.58 | 0.54 |
| 160000 | 1.56 | 1.30 | 1.16 | 1.08 |
| 320000 | 3.17 | 2.63 | 2.34 | 2.17 |
| 640000 | 6.47 | 5.33 | 4.71 | 4.34 |
| 1280000 | 13.19 | 10.79 | 9.49 | 8.71 |
| 2560000 | 26.86 | 21.83 | 19.11 | 17.47 |
| 5120000 | 54.71 | 44.18 | 38.47 | 35.05 |
| 10240000 | 111.39 | 89.38 | 77.46 | 70.31 |
| 20480000 | 226.73 | 180.81 | 155.94 | 141.02 |
| 40960000 | 461.33 | 365.72 | 313.93 | 282.86 |
| 81920000 | 938.42 | 739.64 | 631.96 | 567.36 |
| 1.64E+08 | 1,908.35 | 1,495.66 | 1,272.12 | 1,137.99 |
Table 3. Scalability by Input Size and Processor Speeds (B=2.5
MBPS)
From Table 1, we know that MergeSort is an I/O intense program.
Tables 2 and 3 illustrate that upgrade to a faster file system
can improve the overall processing time more than upgrading the
processor.
Note that the processing parameters W and B may not scale linearly due to swapping and other factors. However, modern processing and input/output hardware devices are fast enough that these imprecision can be either tolerated or compensated using simple statistical techniques. Note also that the computational experiments are only necessary if one needs the best possible prediction. Empirical data can often be used if only qualitative measures are needed.
Unlike a sequential program, a parallel program is associated with greater development expenses and illusive potential. The key problem is that there are more performance sensitive parameters in parallel processing than that in sequential programming. However, using simple extensions to the above scalability analysis method, we can establish a parallel program scalability analysis method called steady state timing models.
In traditional parallel program evaluation, Amdahl's law [1] has been most widely used:
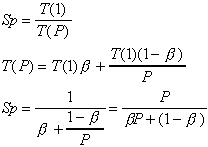
where Sp is speedup, T(1) is the execution
time using one processor, T(P) is the execution
time using P processors, 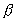 is the percentage of total serial part of the program. Thus (
is the percentage of total serial part of the program. Thus (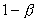 )
of the program can be processed in parallel using P
processors.
)
of the program can be processed in parallel using P
processors.
A cursory reading of Amdahl's Law may result in an assumption
that 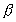 is a constant for a given serial
program. This assumption is incorrect. Gustafson [3]
first recognized that the percentage of total serial part
is a constant for a given serial
program. This assumption is incorrect. Gustafson [3]
first recognized that the percentage of total serial part 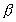 is a function of the number of processors P. Gustafson's
formulation attempts to calibrate the sequential execution time
T(1) based on the parallel execution time T(P).
This is shown as follows:
is a function of the number of processors P. Gustafson's
formulation attempts to calibrate the sequential execution time
T(1) based on the parallel execution time T(P).
This is shown as follows:
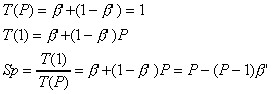
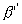 is a ratio between the sequential portion
elapsed time and the total elapsed time using P
processors. The erroneous assumption of
is a ratio between the sequential portion
elapsed time and the total elapsed time using P
processors. The erroneous assumption of 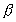 equates this percentage to a ratio between perceived pure sequential
portion elapsed time and the total elapsed time using a single
processor. The error is that the perceived parallel portion can
only be defined when P is known.
equates this percentage to a ratio between perceived pure sequential
portion elapsed time and the total elapsed time using a single
processor. The error is that the perceived parallel portion can
only be defined when P is known.
To see the differences, let P=10, a parallel execution
results 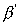 =0.6, namely 40%
of the elapsed time is spent on parallel processing (using 10
processors) and 60% is for sequential processing. If we considered
=0.6, namely 40%
of the elapsed time is spent on parallel processing (using 10
processors) and 60% is for sequential processing. If we considered
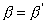 , the Amdahl's law would predict Sp
= 10/(6.4) =1.6 while Gustafson's law gives Sp =
10 - 5.4 = 4.6.
, the Amdahl's law would predict Sp
= 10/(6.4) =1.6 while Gustafson's law gives Sp =
10 - 5.4 = 4.6.
This difference disappears if we compute 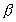 according to the correct assumption. For example, let 10
seconds be the total elapsed time for the parallel algorithm that
gives the
according to the correct assumption. For example, let 10
seconds be the total elapsed time for the parallel algorithm that
gives the 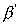 measure. The total sequential
elapsed time for the same algorithm should be 46 = 4 10
+ 6 seconds. This yields
measure. The total sequential
elapsed time for the same algorithm should be 46 = 4 10
+ 6 seconds. This yields 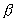 = 6/46 = 0.13. Then the Amdahl's law gives the identical
result: Sp = 10/(1.3+0.87) = 4.6.
= 6/46 = 0.13. Then the Amdahl's law gives the identical
result: Sp = 10/(1.3+0.87) = 4.6.
However, regardless of their equivalence, both laws are too simple
to be useful in parallel program scalability analysis. There are
three considered deficiencies:
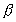 or
or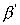 . Many practical programs
contain variable degrees of parallelism that cannot be precisely
modeled using simple percentages.
. Many practical programs
contain variable degrees of parallelism that cannot be precisely
modeled using simple percentages.
The importance of scalability analysis has long been recognized.
In 1980, Ruby Lee defined a model of efficiency, utilization and
quality for parallel programs [6]. This model
intends to grasp the quality of a parallel program as a ratio
of efficiency speedup and redundancy (extent of parallel workload
increase). This definition ignores the possibility of non-search
space compact algorithms (see Section 2) that can require
less parallel workload than their sequential counter-parts. The
model also lacked processor and communication capacity specifications.
Harmonic mean speedup [4] considers a parallel
computer with n processors executing m
programs in various modes with different performance levels. The
harmonic mean performance of such multimode computer is a measure
using a weighted distribution. The use of the weighted distribution
gives too much latitude that permits one to "bend" the
analysis results (towards either in favor of using more processors
or in favor of using fewer processors).
Scalability metric [5] concerns with a
list of attributes that are considered important to the scalability
of a parallel computer system. It can help to guide parallel program
development. However, it lacks a generic analysis tool.
Scalability definition [7] was based
on the ratio of the asymptotic speedup of an algorithm on a real
machine to the asymptotic speedup on an ideal realization on an
EREW PRAM (Exclusive Read Exclusive Write Parallel Random Access
Machine). It does not include any resource specifications, such
as processor and network capacities. However, carefully applying
this method had found that communication latency is inversely
related to scalability [5].
The LogP model [8] tracks the communication
overhead by analyzing detailed message passing patterns and latencies.
It has been used to demonstrate the negative effects by the use
of massively many processors [8]. It does
not include processing time modeling.
Trace driven simulation systems use computer generated trace information
from running a parallel program to track the inter-dependencies
of all overheads. It has been useful to identify architecture
dependent bottlenecks. However, the cost of such an approach is
prohibitively high. The lack of a generic evaluation method makes
them useful only for restricted purposes.
According to [5], the evolution path of scalable computers includes the following measures:
These measures are influenced by many hard-to-control factors ranging from program decomposition method, compiler efficiency to hardware features.
Given a running parallel program, the key performance contributing
parameters of a parallel processing environment are: P
(number of processors), W (processing capacity of
every processor), B (disk I/O rate), and u
(network capacity). Similar to sequential program scalability
analysis, we treat these as customized parameters
that can be significantly different from manufacturer's specifications.
W includes all effects of advanced multiple functional
unit, memory and cache support under the influence of the quality
of a compiler. B includes disk caching and possible
parallel access support, such as provided by the RAID (Redundant
Array of Inexpensive Disks) systems. u includes
hardware protocol and messaging support effects. It denotes the
worst-case latency when all processors are transmitting.
For example, if u=10,000 bytes per second, we expect
the network to transmit 10,000 bytes in 1 second and 0.5 second
for 5,000 bytes even if all processors are transmitting at the
same time. It reflects the worst-case deliverable bandwidth
and latency.
Similarly, the parallel program can be characterized by: size
of the problem (n) it solves, computing density
(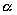 ), communication density (
), communication density (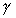 )
and disk I/O data density (
)
and disk I/O data density (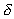 ) per input.
Since these are time independent parameters and can be estimated
or measured easily in the serial program.
) per input.
Since these are time independent parameters and can be estimated
or measured easily in the serial program.
A steady state speedup model is a ratio between
steady state timing models for sequential and parallel algorithms
solving the same problem. Since the timing models project all
effects into the time domain, the speedup model captures the global
interdependencies of all parameters in one equation. An efficiency
model can then be obtained (Eff = Sp/P). If
the models are precise, the analysis accuracy is only affected
by the values of parameters.
The speedup and efficiency models are used to generate performance
maps for the given parallel program (and the serial program).
These maps reveal speedup and efficiency behavior of the program
under any combinations of algorithmic and processing parameters.
Generally, it is hard to develop an abstraction for a parallel program running on multiple parallel processors because there are an explosive number of possibilities with a wide variety of structures. However, from the view point of quantifying the intrinsic dependencies among the key performance contributing parameters of a running parallel program, we can relate all parameters in the time domain by introducing resource capacity specifications as we have done for the sequential program scalability analysis.
In this paper, we use five examples to illustrate the application
of steady state timing models. They disclose some counter-intuitive
results of well-known algorithms.
Sequential and parallel program examples in this paper have been
compiled and run using a cluster of workstations and the Synergy
parallel programming system. Example programs and performance
data can be retrieved via: .
In steady state timing analysis we are looking for the lower bound
(best-case) parallel execution time (assuming the best load balancing),
if the algorithm is solution space compact (see Section 2.1).
Otherwise the timing prediction will be the upperbound (worst
case) elapsed time. The results are expected to be correct within
a constant error in the context of all assumptions.
Throughout this paper, we use the following notations:
We define a base algorithm as a sequential algorithm solving
a problem of interest. A correct parallel implementation of the
base algorithm should generate identical outputs as the serial
algorithm for all possible inputs. In general, there exists at
least one correct parallel implementation for every serial algorithm.
Conversely, there exists at least one correct serial equivalent
(base) algorithm for every possible parallel algorithm.
We base our parallel implementations on the three forms of parallelism
related to those of Flynn[13] and others
[12].
In this paper, SIMD and SPMD, MIMD and MPMD are synonyms. Note
that this treatment is different from hardware classifications
that consider SPMD as MIMD running multiple copies of the same
program.
We define that speedup is a ratio between a base serial
(not necessary the best) program's execution time and its parallel
implementation's execution time, e.g. Sp = Tseq/Tpar.
There are three possibilities:
Considering the inherent overheads in parallel processing, we
identify two factors for linear and superlinear speedups:
It is relatively easy to create a large program and report a linear
or superlinear speedup while the runs using single and smaller
number of processors suffer from insufficient resources, such
as memory or cache. We consider this an "unfair" practice.
In order to identify parallel algorithmic advantages, we prefer
"fair" speedup bases -- sequential runs without resource
constraints.
Note that an "unfair" speedup is in fact an advantage
of parallel processing in that the partitioned parallel programs
are typically much less demanding on local resources than their
serial counterpart.
Definition 1. A sequential algorithm
is search space compact (SSC) if all possible parallel
implementations of the same algorithm must require equal
or more total number of calculation steps (including those in
parallel) for all inputs.
Definition 2. A sequential algorithm is non-search space
compact (NSSC) if there exists at least one parallel
implementation of the same algorithm, computing at least
one input, that requires less total number of calculation steps
(including those in parallel) than the total pure sequential steps.
Note that the emphasis of implementing the same serial
algorithm in parallel restricts the freedom of parallel implementation
only to realizing application dependent SIMD, MIMD and pipelining
parallelisms. This restriction applies to both serial to parallel
and parallel to serial program transformations.
Definition 3. A certificate is a verification algorithm
that given a solution to a problem it can verify if the solution
is correct or not.
Theorem 1. Let the complexity of a certificate be f(n)
and solution algorithm g(n), the solution algorithm
is NSSC if
Example: An O(n2) comparison-based sort
algorithm is non-solution space compact, since the sort verification
algorithm requires O(n), we find
In particular, suppose that a serial algorithm requires n2
comparisons to produce a sorted output. Then
In (2.1), the left-hand-side represents the worst-case number
of comparisons of the serial sort algorithm, right-hand-side represents
the total worst-case parallel computing steps are:
There is an apparent reduction in parallel comparison steps!
This implies the possible superlinear speedup in parallel execution.
This "magical power" of instruction reduction comes
from the way we define our speedup. The multiplicative
power of nonlinear functions is the source of "parallel instruction
reduction". Such reduction exists in all serial algorithms
that are amenable to a divide-and-conquer strategy using exclusively
partitioned inputs. Further, for every such NSSC algorithm,
there exists an optimal number of partitions of input such that
the total number of computing steps is minimized.
On the other hand, an O(nlgn) sort algorithm is
SSC since we cannot find an
Corollary 1. All NP-Complete algorithms are non-solution
space compact.
Proof:
One condition for an algorithm to be in the NP-complete class
is that there exists a certificate that given the solution it
can verify the solution in polynomial time [11].
All NP-complete algorithms require exponential time complexity.
The conclusion follows.
Matrix multiplication algorithms are SSC. NP-hard optimization
algorithms are SSC. However, for algorithms using branch-and-bound
heuristics, the sub-problems are NSSC. Therefore, it is possible
for these algorithms to achieve superlinear speedup on selected
inputs.
The SSC and NSSC classifications are also applicable to parallel
algorithms designed only for parallel machines, such as the line
drawing algorithms (SSC) for the massive parallel processor CM2
[9] and the parallel sort algorithms [12]
(SSC).
Note that the NSSC's "parallel instruction reduction power"
can be eliminated if we use a "strictly fair" comparison
base. For example, for parallel sort, computing speedup using
a serial algorithm with the same partitioning factor (a
serial divide-and-conquer algorithm) as the number of parallel
processors can eliminate superlinear speedup (see Section 3).
For optimization algorithms, superlinear speedup can be eliminated
if we force the sequential algorithm to following the best parallel
search path.
However, in practice, it is inconvenient to alter a serial algorithm
whenever we add a processor (for the parallel sort ) or change
an input (for optimization algorithms) for performance evaluation.
In this paper, we prefer speedup be computed using a "fair"
sequential run. Theoretically, superlinear speedup is then only
possible for NSSC algorithms. For SSC algorithms delivering superlinear
speedups, we know immediately that there is a resource factor
in the comparison basis.
The conventional program time complexity analysis investigates
the asymptotic order of execution steps of a program as a function
of its input size. The steady state timing model of a program
characterizes its asymptotic execution time as a function of performance
critical parameters in addition to the input size. In this paper,
we use the following:
For convenience, we also use MIPS (Million Inputs Per Second),
KBPS (Kilo-Bytes Per Second) and MBPS (Million Bytes Per Second)
as aggregate measures.
For a sequential program, the timing model is merely an equation
in the following form:
Similarly,
For the parallel program solving the same problem, the timing
model contains four basic parts:
where Tcomp is for pure parallel calculation (this corresponds
to the
Tsync accumulates all possible waiting times due to serial dependencies.
There are two kinds of waiting time:
In this paper, the dynamic waiting time is set to zero to provide
an upper bound for evaluating various load balance schemes.
Having the sequential and parallel timing models, we can easily
obtain the speedup and efficiency models as follows:
Parallel algorithm scalability analysis is to investigate the
performance map generated by values of Sp and Eff
under varying algorithmic and processing parameters. Note that
for NSSC algorithms we may have Sp >> P and
Eff >> 1.
Suppose that we are to internally sort a large data set. We have
access to a few supercomputers linked by high speed networks and
to a few workstations linked by a slow network. We ask if it is
worth splitting the data via the network to multiple processors
and then merge the results in each of these environments?
Let us use randomized Quicksort [11].
Assuming balanced partitioning and
The first term is the pure computing time. The second term is
the summation of disk read and write times.
Using the split-sort-merge scheme, we then have a parallel sorting
model:
The first term is the computing costs for splitting, parallel
sort and merging. The second term is disk I/O. The third term
is the total communication cost.
Table 1 is produced using (3.1) and (3.2) with assumptions representing
a networked supercomputer system. It illustrates the fact that
larger input size has little impact on improving speedup
under current assumptions. In this table all measurement units
are in seconds, except for n and Sp.
2. Preliminaries
and Limitations
n : Input size,
P : Number of processors,
Sp : Speedup, and
Eff : Efficiency = Sp/P.
SI(P)MD : Single Instruction (or Program) Multiple Data
MI(P)MD : Multiple Instruction (or Program) Multiple Data, and
Pipeline : Sequentially dependent multiple processors processing
multiple consecutive data sets.
2.1 Superlinear Speedup
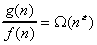 , for all n>0
and some
, for all n>0
and some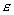 > 0.
> 0.
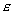 = 1.
= 1.
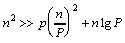 , for all n > P >2.
(2.1)
, for all n > P >2.
(2.1)
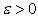 .
.
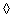
2.2 Steady State Timing Models
P : Number of processors.
W : Customized processor power (in number of inputs per second).
u : Network capacity (in bytes per second).
B : Disk speed (in bytes per second).
n : Size of problem input.
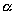 : Computing density (in instructions per input).
: Computing density (in instructions per input).
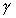 : Communication density (in bytes per input).
: Communication density (in bytes per input).
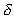 : Disk access density (in bytes per input).
: Disk access density (in bytes per input).
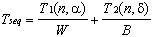 . (2.2)
. (2.2) 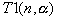 is the total number of instructions required
to solve a problem of size n.
is the total number of instructions required
to solve a problem of size n. 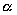 denotes
the average calculation steps per input. Different input can change
denotes
the average calculation steps per input. Different input can change
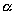 without altering the problem size (n).
For example, complex domains (-2, -2) (2,2) and (-0.1,-0.1) (0.1,0.1)
for a Mandelbrot set displayed on the same screen size can result
in drastically different total execution times (Section 8). For
other algorithms,
without altering the problem size (n).
For example, complex domains (-2, -2) (2,2) and (-0.1,-0.1) (0.1,0.1)
for a Mandelbrot set displayed on the same screen size can result
in drastically different total execution times (Section 8). For
other algorithms, 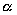 can be a constant function
implying that the total calculation steps remain the same for
all inputs. Matrix multiplication is an example (Section 5).
can be a constant function
implying that the total calculation steps remain the same for
all inputs. Matrix multiplication is an example (Section 5).
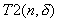 is the total disk access volume
of the program. If not dominating, we omit T2
in subsequent discussions.
is the total disk access volume
of the program. If not dominating, we omit T2
in subsequent discussions.
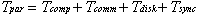 (2.3)
(2.3)
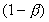 part in Amdahl's law), Tcomm is
for pure communication, Tdisk is for disk access (possibly in
parallel) and Tsync is for program-to-program synchronization.
A similar formulation for parallel programs can be found in [19].
part in Amdahl's law), Tcomm is
for pure communication, Tdisk is for disk access (possibly in
parallel) and Tsync is for program-to-program synchronization.
A similar formulation for parallel programs can be found in [19].
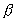 part in Amdahl's law.
part in Amdahl's law.
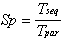 , (2.4)
, (2.4)
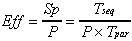 . (2.5)
. (2.5)
3. Sorting in Parallel
3.1 An O(nlgn) Sorter Using Supercomputers
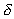 =
8 bytes (size of the sort key), the sequential timing model is:
=
8 bytes (size of the sort key), the sequential timing model is:
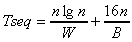 . (3.1)
. (3.1)
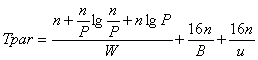 . (3.2)
. (3.2)
| 1.00 | ||||||||
Table 4 also illustrates an important utility of the timing models:
visualization of the quantitative overhead changes. In this
case, the apparent impeding friction is disk I/O.
In order to find the best parallel processor/network configuration
for this application, Figure 2 shows the performance map of the
parallel sorter using three processors with varying uni-processor
power and networking speeds (P=3, n = 1018
and = 8).
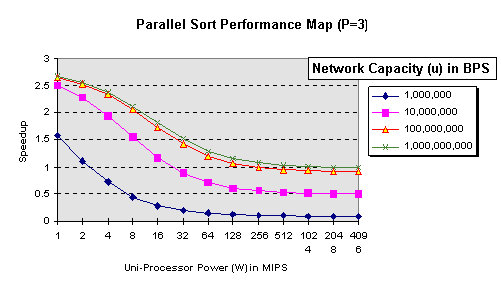
Figure 2 illustrates that good speedup is promised if connecting
low power processors (<= 1 MIPS) on a fast network
(>=100 MBPS). For any network speed, parallel
sort using multiple networked fast processors (W > 128
MIPS), a slow disk (10 MBPS) and an O(nlgn)
algorithm is not worthwhile.
We can also use these results to investigate possible improvements.
For example, we can reduce disk I/O time by changing the second
term of (3.2) from 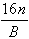 to
to 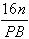 .
Since P is small, we quickly realize that this will
not affect the overall conclusion. However, if the disk system
is significantly faster (say 100 times B), this
conclusion will change (see next section).
.
Since P is small, we quickly realize that this will
not affect the overall conclusion. However, if the disk system
is significantly faster (say 100 times B), this
conclusion will change (see next section).
Since speedup is a ratio between sequential and parallel running
times, inefficient serial programs can result in better speedups
(smaller W's). In this section we show how to demonstrate
superlinear speedup using a cluster of workstations and an O(n2)
sorter.
The sequential and parallel models are as follows:
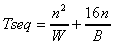 , (3.4)
, (3.4)
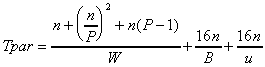 . (3.5)
. (3.5)
Table 2 shows the predicted (using (3.4) and (3.5)) and achieved
speedups using a non-dedicated cluster of 2-5 DEC Alpha workstations.
In this environment, uni-processor power W=5MIPS,
network capacity (a low-end Ethernet) u=60,000 BPS
and disk I/O capacity B=3.5 MBPS (NFS mounted via
Ethernet).
| Problem Size (n) | ||||||
|
|
|
| ||||
For this environment, larger problem sizes caused better speedups.
The lower uni-processor power (5 MIPS) has caused the higher computing/IO
and computing/ communication ratios.
As mentioned earlier, superlinear speedup would be impossible
if we insisted on the best serial program as the comparison basis.
For example, partitioning the input in the serial program should
improve the sequential execution performance without using parallel
processors. Table 3 shows the elapsed times (in seconds) by dividing
and solving the problem in 2 and 4 subsets using one processor.
This explains why any O(n2) sort algorithm
is NSSC (non-search space compact).
Table 6. Elapsed Times of Sequential Sorter Using Partitions
Finally, as suspected, in this processing environment a single
workstation using an O(nlgn) algorithm can beat
the best multi-processor run using O(n2)
algorithms.
MPP stands for Massively Parallel Processing. It denotes the use
of many fine grained parallel processors. One often wonders if
a given program can effectively take advantage of all these processors.
We use an embarrassingly parallel example to quantify the efficiency
loss when using many processors even with little communication
overhead and very high computing density.
This example involves plotting a fractal image of (x,y)
resolution. This requires calculating the color indices of n
= x y pixels. The color of each pixel represents the orbit
length of a corresponding complex point based on a simple equation
(such as Fatou's). Since each pixel can be calculated entirely
independent of all others, we can use as many processors as pixels.
Further, parallelism exists at many grain levels -- we have at
least three ways to split the calculations: by pixel, by rows
or columns, and by tiles. Many graphics, image processing and
numerical programs share the same characteristics as this example.
We investigate the following: Is it possible to achieve linear
speedup (Sp = P) for a "smart" parallel
implementation? Can this program benefit from massively many processors?
In this case, given a complex domain, 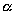 refers to the average computing steps required per pixel,
refers to the average computing steps required per pixel, 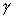 refers to the average number of data bytes (both in and out) per
pixel. Assuming that the local memory latency is negligible, the
model is:
refers to the average number of data bytes (both in and out) per
pixel. Assuming that the local memory latency is negligible, the
model is:
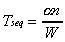 . (4.1)
. (4.1)
This is an obvious SSC algorithm. Therefore, linear speedup is
only possible if we use "unfair" bases.
In the parallel timing model, assuming 1 < P n, the pure computing time is:
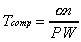 .
.Since there is no cross data sharing, the total fractal communication time is:
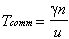 .
.Assuming further that all processors can terminate at the same time, dynamic synchronization time is zero. No static synchronization exists; thus Tsync = 0. The parallel execution time is:
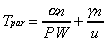 . (4.2)
. (4.2)Speedup can be decided:
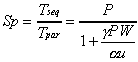 . (4.3)
. (4.3)The efficiency is:
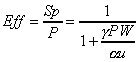 . (4.4)
. (4.4)From (4.3) and (4.4), we can conclude the following:
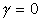 , linear speedup is impossible.
But
, linear speedup is impossible.
But 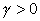 for all meaningful parallel implementations.
This confirms the SSC characteristics.
for all meaningful parallel implementations.
This confirms the SSC characteristics.
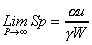 . This tells
that the weaker the individual processor power (or worse
the compiler and operating system, since W is a
customized measure), the better the speedup.
. This tells
that the weaker the individual processor power (or worse
the compiler and operating system, since W is a
customized measure), the better the speedup.
 )
and a parallel processing environment (by u and
W), the coarser the parallel grain (larger
)
and a parallel processing environment (by u and
W), the coarser the parallel grain (larger 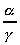 ratio)
the better speedup and efficiency.
ratio)
the better speedup and efficiency.
In order to find a desirable aggregate processor power, Figure
3 shows the processor powers using different uni-processors and
inter-connection network speeds (varying W and u)
for fractal computing. In this calculation, we assumed P=512,
computing density 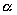 =32,000
(instructions per pixel), communication density
=32,000
(instructions per pixel), communication density 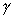 =8
(number of I/O bytes per pixel).
=8
(number of I/O bytes per pixel).
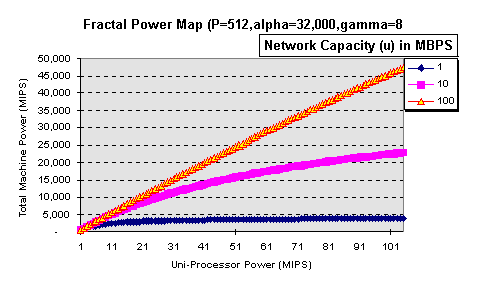
Figure 3 suggests that as long as we have fast interconnection
network, MPP is a way to acquire larger computing powers. However,
the efficiency map suggests something else (Figure 4).
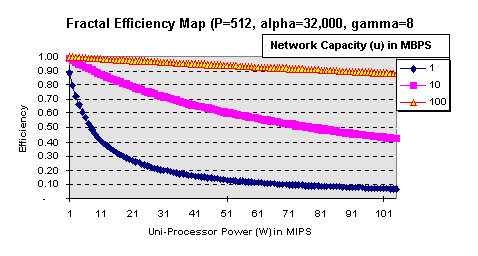
An 87% efficiency level can be obtained if we use 512 101 MIPS
processors with a sustained 100 MBPS network. The use of higher
power uni-processors or the use of greater than 512 processors
must generate lower efficiency. Also note that these numbers change
as the input () changes. This result also implies unless a parallel
program is only to process one particular input, it should not
rely on a fixed number of processors (logical or physical).
Furthermore, improving the 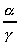 ratio
is critical to good performance. Since
ratio
is critical to good performance. Since 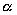 is determined by a given input, wiring one processor to each pixel
is detrimental to parallel performance (due to larger
is determined by a given input, wiring one processor to each pixel
is detrimental to parallel performance (due to larger 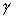 see Section 9 for details). This is an argument for coarse-grain
parallel processing and against fine grain partitioning techniques.
This argument also challenges the use of MPP since it is impossible
to make efficient use of massively many processors (> 512)
even for this "best-case" application.
see Section 9 for details). This is an argument for coarse-grain
parallel processing and against fine grain partitioning techniques.
This argument also challenges the use of MPP since it is impossible
to make efficient use of massively many processors (> 512)
even for this "best-case" application.
The "mainstream" parallel processing culture has been on the fine-grain side [16] even though communication overhead analysis showed adverse effects using too many processors [5] and [8]. Using the same interconnection network technology, we can build more efficient parallel processors using a fewer high power uni-processors than using massively many weaker processors. It seems that as the uni-processor power increases, there is a clear need to re-evaluate fine grain parallel processing techniques.
It is usually hard to compare parallel programs. Using steady
state timing models, parallel programs can be related by their
performance behaviors.
A Monte Carlo simulator typically uses a simulated time (t)
that is absent in the previously defined notations. In this case,
the size of the problem (n) is the number of units
being simulated, e.g., financial instruments, molecules, bodies,
etc. In this section, we assume a "typical" Monte Carlo
simulator in that for each simulated time slice, the unit computations
are independent and data sharing mutually exclusive. Dependencies
exist between time slices.
The sequential timing model for this Monte Carlo simulator, without disk I/O, is:
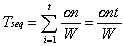 . (5.1)
. (5.1)
In this case, 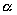 refers to the average number
of computing steps per simulated object per time slice and
refers to the average number
of computing steps per simulated object per time slice and 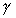 refers
to the average number of bytes required for input and output per
object per time slice.
refers
to the average number of bytes required for input and output per
object per time slice.
The parallel timing model, 1 < P n, can be expressed as:
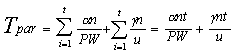 . (5.2)
. (5.2)
Note that (5.2) includes Tsync in the two summations.
The speedup and efficiency are:
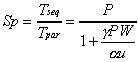 . (5.3)
. (5.3)
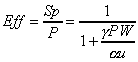 . (5.4)
. (5.4)
Note that (5.3) and (5.4) are identical to (4.3) and (4.4). Therefore,
a Monte Carlo simulator should have same performance behavior
as a fractal program that is much simpler in structure.
Performance comparisons can help to detect design and coding mistakes. For example, when designing computational experiments, we should notice that both the number of simulated objects and the length of simulated time should have no impact on the speedup and efficiency (unless one wants to manufacture good performance reports with unjustified comparison bases).
Matrix multiplication is frequently used in many science and engineering programs. Its common sequential algorithm is as follows. Let A, B and C be n*n matrices and C is initialized to zero:
1. for i=1 to n 2. for j=1 to n 3. for k=1 to n 4. C[i,j] = C[i,j] + A[i,k] * B[k,j] 5. end 6. end 7. end
Line 4 is also called the "dot product" that can be
performed independently for each entry in C. This is an SSC algorithm
as discussed earlier.
The sequential timing model is:
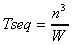 (6.1)
(6.1)
For parallel implementations, there are two types of messages:
exclusively read and cross shared. Each dot product must use one
row of A and one column of B. To prevent doing redundant work,
one of them (let's say A) must be mutually exclusively distributed,
such that no two processors would get the same row. This amounts
to n2 exclusively readable data items
on the network. The other matrix (B) must be broadcast to all
processors. This requires at most Pn2 data
items on the network (assuming no hardware broadcast support).
For networks with hardware broadcast support, this may be reduced
to O(n2). Using steady state timing models,
instead of calculating message delays, we need the total communication
volume. This simplifies the modeling process.
Assuming double precision arithmetic (8 bytes per number), the parallel timing model is then:
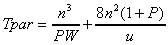 (6.2)
(6.2)The speedup model is:
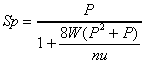 (6.3)
(6.3)
This is one of those earliest programs with well documented parallel
performance results. (6.3) can be used to validate all published
matrix multiplication performance results.
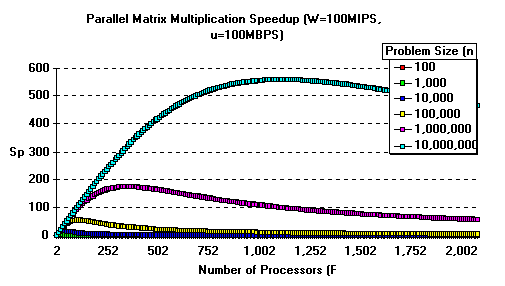
Figure 5 shows the typical speedup map of this system without
hardware broadcast support: speedup deteriorates quickly as P
increases. This is an example of algorithms with high order computing
complexity (n3) and lower order communication
complexity (n2). Therefore larger problem
size (n) can compensate for the communication costs.
The benefit of using steady state models is that we can visualize
the order changes and predict the speedup "bumps" prior
to programming.
Algorithms for solving linear or non-linear equation systems require large number of serially dependent steps. The key characteristics of this application group are fine grain, dynamic parallelism and frequent communication.
For a linear system Ax=b, Gaussian elimination can
be used to find the solutions directly or a factorization of A,
such that A=LU where L is a lower-triangular
matrix and U is an upper-triangular matrix [10].
Once A is factorized, we can quickly find solutions
for different constraints (b's).
Gaussian elimination involves eliminating unknowns one column
at a time until we obtain an none-zero upper-triangular matrix
(and a lower-triangular matrix of multipliers for LU factorization).
We consider the elimination of a column a wave of calculation.
There are (n-1) waves in total with the first wave
of size (n-1). The second wave must not proceed
until the corresponding unknowns are solved in the first wave.
The overall triangularization algorithm is to process waves of
sizes: (n-1), (n-2), ..., 1.
The variable elimination at each column can be processed in parallel.
The largest independently computable row requires 3 n
multiplication. This number reduces as the program progresses.
This is an NSSC algorithm since it's verification algorithm is
of a polynomially smaller complexity.
The sequential timing model is:
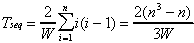 . (7.1)
. (7.1)Assuming there are 1 < P n processors. Each processor can eliminate an independent variable within a column. Tcomp is:
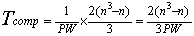 .
.For each wave i, the size of data volume is 28(n-i)2 (assuming double precision arithmetic), because each processor must take a row in A and return the revised row to update A. We have Tcomm as follows:
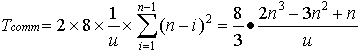 .
.Further, since the static synchronization is accounted for in the summations of Tcomp and Tcomm, we have Tsync = 0. The parallel timing model is then:
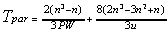 . (7.2)
. (7.2)The speedup model is:
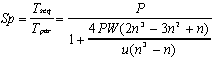 . (7.3)
. (7.3)
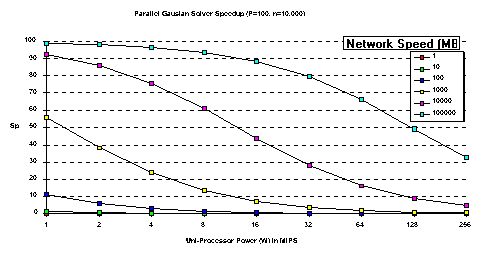
The inhibiting factor for this parallel implementation is the
O(n3) communication volume.
Unless the network speed u >> PW (7.3), the
total parallel processor power, the communication overhead offsets
all benefits of parallel processing (see the < 100 MBPS lines
in Figure 6). Current technological trends indicate that P
W can easily exceed u.
Greater efficiency can be brought by using a smaller number of
processors and some algorithmic improvements. [2]
shows that it is possible to use a divide-and-conquer strategy
(block factorization) to reduce the communication volume to O(n2)
with a large constant. This algorithm would then
have the similar performance behavior as the matrix multiplication
algorithm.
Synchronous and asynchronous iterative solvers are SSC since their verification and solution algorithms are of the same order. The use of steady state models helps to quantify the frequency of communication in order to obtain the best possible overall processing time [17].
Parallel processing grain size affects two major forms of overhead:
communication and synchronization. Fine grain parallel processing
permits a large number of independent processors at the expense
of increased communication overhead. Coarse grain parallel processing
saves communication overhead while risking synchronization penalty
[20]. Since the computing density of a
process is input dependent, the synchronization overhead exists
for parallel computers using homogeneous and heterogeneous processors.
In the following discussion, we identify the best grain sizes
assuming the best load-balancing. In order to achieve the optimal
performance, it is necessary to adapt the identified solutions
using practical load-balancing algorithms [20].
Defining the best parallel processing grain used to be an architecture
dependent problem. Namely, one must first understand the features
of a parallel processor before deciding the "best fit"
between the application and these features. It was necessary since
older parallel processors typically used low power uni-processors
with small local memories.
As low-cost high performance commodity uni-processors become widely
available, this "old-fashioned" programming paradigm
needs an re-evaluation, especially with the decreasing cost of
memory devices. In order to find the true potential of an algorithm,
we prefer finding the best possible parallel performance before
compromising to architecture specific restrictions. This will
give us the "big picture" with marked costs for
the compromising details.
For example, a typical Mandelbrot fractal program has three nested
loops as follows.
Input:
a (magnifying glass real coordinate), b (magnifying glass complex coordinate), size (magnifying glass size), limit (maximal visible colors), n (display resolution)
Program:
1. for i=1 to x 2. ca = a + i * size/x 3. for j=1 to y 4. zx = 0 5. zy = 0 6. count = 0 7. cb = b + j * size/y 8. while ((zx*zx+zy*zy)<4) and (count < limit) 9. count = count + 1 10. nzy = 2 * zx * zy + cb 11. zx = zx*zx - zy*zy+ ca 12. zy = nzy 13. end while 14. plot at (i,j) with color (count) 15. end for 16. end for
The sequential and parallel timing models are shown in (4.1) and
(4.2).
In search for the largest computing/communication ratio, we study
the factors that impact communication overheads since the computing
density is determined by the given input.
First, given problem size, for this program the result data volume is a constant. Secondly, the work distribution data volume varies according to partitioning strategies. Assuming single precision arithmetic (4 bytes per number), there are at least three partitioning possibilities with varying communication penalties:
Since 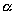 remains the same for a given input
and
remains the same for a given input
and 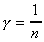 of total communication volume (distribution
+ result data volume), equations (4.3) and (4.4) indicate that
cutting the first loop can produce the largest
of total communication volume (distribution
+ result data volume), equations (4.3) and (4.4) indicate that
cutting the first loop can produce the largest 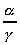 ratio (grain size =n/x=y).
ratio (grain size =n/x=y).
Further, if P << x, packing working assignments
with xy/P columns each can reduce the data distribution
volume to 2 4P (compared to 4x). The
optimal grain size is between [xy/P, y], that should
be determined experimentally according to some load balancing
algorithm.
For Monte Carlo simulators, parallelism does not exist on the
top level (t). The speedup model (5.3) indicates
that the next highest level (n) should be exploited.
(5.3) indicates that P < n is a good choice.
Similar to the fractal program, the optimal grain size is between
[n/P, n/kP], 1 < k < n/P,
adjusted according to some load balancing algorithm.
For parallel sorters, the parallel models (3.2) and (3.5) do not
include the switching costs (time for switching from communicating
with one processor to another). Intuitively the smallest possible
grain size is 1 (implying P=n). In this case, however,
both parallel algorithms degenerate into an inefficient insertion
sort algorithm (O(n2)). To avoid such
degeneration, the only choice left is P < n or
grain size = n/P. It is also desirable to have smaller
P values since it is part of the parallel overhead
((3.2) and (3.5)).
For parallel matrix multiplication, the intuitive grain level
is one dot-product per processor (or P = n2).
However, the parallel timing model (6.2) suggests a large communication
overhead ((n4)) that would offset all
benefits of parallel processing. Similarly, P = n
and other finer grain partitioning are equally undesirable. The
only choices are P < n or grain size > n2/P.
For a parallel Gaussian Elimination program, parallelism decreases
as the calculation progresses. The natural choice is P n
or one variable elimination per processor. Coarser grain parallel
processes can save on communication costs (7.2). Finer grain parallelism
will entail larger communication overhead as illustrated above
(case (c)).
We can conclude from all above examples that the highest
abstraction level that preserves application specific
SIMD, MIMD and pipelined potential is the best parallel processing
grain level. Due to hardware implementation difficulties, this
coarse grain requirement is not well supported by existing parallel
computers. There are many parallel processors that permit high
interconnection capacity only at much smaller grain sizes. The
timing models can then be used to compare the potential speed
difference between the fine and coarse grain designs. The generalization
to other algorithms is straightforward.
For studies of a specific parallel processor, modeling accuracy becomes important. Modeling accuracy is affected by both the model precision and parameter accuracy. Model precision depends on the skills of the modeler. Assuming precise models, this section illustrates practical steps toward obtaining accurate values of algorithmic and processing environment parameters. These values define the base points on the performance maps. Curves can then be generated using respective performance models.
For most algorithms, there are only three time independent
parameters: computing density 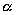 communication density
communication density 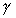 and input/output
density
and input/output
density 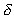 . Values of these parameters can
be obtained by instrumentation statements inserted into the serial
program. Since they are time independent, there is no consequence
for this "intrusion".
. Values of these parameters can
be obtained by instrumentation statements inserted into the serial
program. Since they are time independent, there is no consequence
for this "intrusion".
For example, the value of 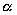 =32,000
in Figure 3 was calculated by counting the total number of operations
for plotting the fractal image of complex domain (1,1) (-1,-1)
divided by the total number of pixels. Similarly
=32,000
in Figure 3 was calculated by counting the total number of operations
for plotting the fractal image of complex domain (1,1) (-1,-1)
divided by the total number of pixels. Similarly 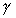 and
and 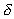 can be obtained.
can be obtained.
Uni-processor capacity W, interconnect capacity
u and input/output capacity B have
time dependent values and are generally difficult to obtain.
We overcome the difficulties by defining them as "customized
measures" for each application. The following steps can ensure
a reasonable result.
By definition, B is the average input/output capacity
in bytes per second. Inserting counting and timing instructions
to the base serial program can get an estimated B
value (typically < 10 MBPS for standard non-dedicated SCSI-2
systems, a little higher for dedicated systems without parallel
support).
Similarly, W is the application dependent average processing capacity of each processor. Due to the inherent differences between parallel and serial processes solving the same problem, assuming heterogeneous processors, we use the following heuristic to capture its value:
For communication capacity (u), we use the following:
These are the upper (u2) and lower (up)
bounds of u. For SSC algorithms, negative u
(communication) values indicate under-estimated W(processor
capacity). For NSSC algorithms, we have to find an input instance
that would force the parallel system to follow a close-to worst-case
search path and re-run the tests.
For most existing multi-processor systems, the input/output capacity
B is also dependent on P, since they
share the same network. One can then obtain the upper (B2)
and lower (Bp) bounds of B
using the similar procedure for u.
These values define the base points on the performance maps. Multi-scenario analysis can then be conducted using any values between the upper and lower bounds. If the goal is only to have qualitative conclusions, we can omit detailed statistical analysis. Otherwise, one can use various distributions to approximate the actual behavior of W, u and B. The timing models can then be applied to each time step.
Steady state timing models are found uses in the following situations:
These assessments can guide effective parallel system development
preventing costly mistakes in early stages.
A parallel program has the potential to accelerate its processing
speed. However, it also embodies new forms of friction that cannot
be well understood using conventional program analysis methods.
Unlike sequential programs whose resource use complexities can
be analyzed before programming, a parallel program often relied
on programming experiments to explain its behavior. The results
of experimentation were only of limited value since they contained
uncontrolled factors ranging from programming style to hardware
features. For exactly the same reasons, parallel programs could
not be easily compared.
The steady state timing method simply relates the non-orthogonal
parameters in the time domain by introducing resource capacity
specifications. It is worth noting that as the speeds of computing,
communication and input/output devices improve, the accuracy of
steady state models increases.
In this paper, we have used steady state timing models to reveal
a few important insights in parallel processing: finding the best
processor/network configuration, finding the best grain size and
parallel program comparison. These results have important practical
implications. For example, since there is an optimal processor/network
configuration for each application input, parallel programs should
not include direct manipulation of processors since the optimal
number of processors will change as the input changes. For parallel
compilers, since the best processing grain is found at the top-level
abstraction, the new emphasis should be, in addition to existing
local optimization schemes, to analyze the top-level data dependencies
and gradually "dig" down to finer grains only if the
network can sustain the increased traffic.
The use of steady state timing models encourages the discovery
of application specific performance features as opposed to architecture
specific features. This suggests a discipline in parallel program
design and implementation that can be taught in universities.
The analysis results can also help the hardware engineers to build
more effective parallel architecture that can endure rapid processor
and networking technology changes.
We have used timing models to quantify asynchronous linear system
solver implementations. The results showed that it is possible
to trade the abundance of computing power for limited network
bandwidth by systematically relaxing the data exchange requirements
in parallel iterative algorithms [17].
We have also found that it is possible to quantify the overhead
of fault tolerant techniques for parallel systems such that an
optimal compromise of performance and reliability (performanability)
can be defined [18].
In conclusion, we observe that analytical tools of such nature exist in many engineering disciplines and in sequential programming. For parallel programming to be of wide-spread use, we believe such a tool is necessary. The rapid quantitative improvements in uni-processor and inter-connection network speeds fostered the needs for qualitative changes in parallel programming and system design paradigms. This reported merely makes the needs more explicit.
To my colleagues, Drs. Giorgio Ingargiola, James Korsh, Charles Kapps, Arthur Poe, Xiangcuan Ge, Jianming Zhao, Ruijin Qi and to my students, John Dougherty and Kostas Blathras for proofreading earlier drafts of this paper and for applying the timing model method to their work. To CIS750, CIS669 class students for validating the timing model results using the Synergy parallel programming system.