Parallel Processing of Linear
Systems Using Asynchronous Iterative Algorithms
Kostas Blathras
kostas@thunder.ocis.temple.edu
Daniel B. Szyld
szyld@math.temple.edu
Yuan Shi
shi@falcon.cis.temple.edu
Temple University
Philadelphia, PA 19122
April 1997
Abstract
Iterative algorithms for solving systems of linear equations
require data exchanges at each iteration step due to data dependencies.
When processed in parallel, this requirement forces frequent data exchanges
among parallel sub-tasks resulting in long execution. These dependencies
also prohibit effective parallel program generation by existing parallel
compilers.
Asynchronous iterative algorithms can reduce much of the
data dependencies by using older data received earlier in time. This, however,
can cause an increase in total iterations for the algorithm to converge.
Considering that the total network capacity is typically far less than
the overall computing capacities of multiple processors, the motivation
of this study is to identify the possible time savings by reducing inter-processor
communication at the expense of increased calculations.
In particular, we report a performance study on parallel
implementations of a non-uniform magnetic field simulation program. We
use a time complexity-based analysis method to understand the inherent
interdependencies between computing and communication overheads for the
parallel asynchronous algorithm. The results show not only that the computational
experiments closely match the analytical results but also that the use
of asynchronous iterative algorithms is beneficial for a vast number of
parallel processing environments.
Keywords: Parallel Processing, Asynchronous Algorithms,
Parallel Iterative Methods.
1. Introduction
In this paper we present several aspects of the parallel
asynchronous solutions of linear algebraic systems of the form
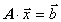 ,
(1)
,
(1)
where 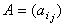 is a large
is a large 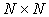 matrix, and x and b are N-vectors. This problem lies
at the core of many scientific and engineering applications. The computational
test problem we use in this paper is that of the determination of the magnetic
field in a region outside of a permanent magnet [10]; see further Sect.
3. Since full direct methods for the solution of (1) require
matrix, and x and b are N-vectors. This problem lies
at the core of many scientific and engineering applications. The computational
test problem we use in this paper is that of the determination of the magnetic
field in a region outside of a permanent magnet [10]; see further Sect.
3. Since full direct methods for the solution of (1) require 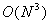 operations and usually sparse methods lack parallelism, we concentrate
in this paper on iterative methods, which are used in practice due to their
reduced time complexity.
operations and usually sparse methods lack parallelism, we concentrate
in this paper on iterative methods, which are used in practice due to their
reduced time complexity.
When developing the parallel iterative algorithms for
the solution of (1), the most difficult problem is the inherent data dependencies.
For example, consider the classical (point) Jacobi iteration method
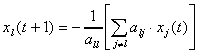 , l=1,2,…N; t=0,1, …;
(2)
, l=1,2,…N; t=0,1, …;
(2)
where t is the iteration index, starting from
an initial vector 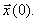 If each of p processors
compute one of the components of x in (2), i.e., p=N, this
implies a very large amount of data "shuffling" between processors at each
iteration. Furthermore, all processors must synchronize at that point creating
a time barrier.
If each of p processors
compute one of the components of x in (2), i.e., p=N, this
implies a very large amount of data "shuffling" between processors at each
iteration. Furthermore, all processors must synchronize at that point creating
a time barrier.
In an asynchronous version of (2), each processor would
compute xl using the most recent information available
from the other processors, i.e., values of xl which may
be older than xj(t), say possibly xj(t-k),
where k would depend on l and j; see further Sect.
2, where we use an equivalent notation. In other words, asynchronous iterative
algorithms do not require exchange of the most recent values. The convergence
of (2) would naturally be delayed by the use of less recent values of xj,
but since no idle time for synchronization is necessary, and less overall
communication takes place, asynchronous algorithms have the potential of
outperforming standard synchronous iterative methods. We should mention
here that, under certain hypothesis, asynchronous iterative methods are
guaranteed to converge to the solution of the linear system (1); see, e.g.,
[9,14].
One of the goals of this paper is to illustrate the applicability
of asynchronous iterative methods. In particular, we want to point out
how these methods can be implemented on inexpensive clusters of workstations,
even personal computers, connected with 10 Mbps shared medium Ethernet.
We use a passive object programming system named Synergy [8], which provides
tuple spaces as communication and synchronization mechanisms. The choice
of this programming tool is discussed in Sect. 4.1.
In practical block two-stage asynchronous iterative methods,
each processor solves a small linear system, not just one equation, as
in (2). Each processor uses an (inner) iterative method, e.g., Gauss-Seidel,
for the approximate solution of the linear system. One of the critical
questions about two-stage methods is what criteria to use to stop the inner
iterations in each processor; see, e.g., [13, 18]. In this paper, we compare
two widely used stopping criteria: one based on the size of the (inner)
residuals, and the other on a fixed number of inner iterations. We report
that a fixed number of inner iterations is a better choice for the architecture
considered in this paper; see Sects. 4.3 and 6.
Another question which we address is load balancing.
Should the partition of the domain be fixed by the number of available
processors (static block allocation) or do we gain by dividing the computational
domain dynamically to account for the different computational complexity
of the tasks in each region? To answer this question we develop a timing
model. Using the timing model, we conclude that when the communication
network is slow, as is the case of the hardware considered in this paper,
the static block allocation is preferred. It follows as well, that a dynamic
block allocation would be preferable for faster networks; see Sects. 4.4
and 6.
We report on a systematic procedure for identifying the
optimal data exchange for a given asynchronous iterative algorithm and
parallel processing environment. Our experience showed that it is possible
to gain speed using asynchronous algorithms and clusters of workstations
on a slow Ethernet. Our scalability models also show that asynchronous
algorithms are beneficial for all parallel environments in which the sum
of multiple processors' capacity (in instructions per second) far exceeds
the sum of networking capacities (in bytes per second).
The overall organization of this paper is as follows.
In Sect. 2, we describe the applicable class of asynchronous iterative
algorithms. In Sect. 3, we describe the computational test problem used
in this study. In Sect. 4, we detail the asynchronous parallel program
design and implementation. In Sect. 5, we present timing analysis for evaluation
of various implementation alternatives. In Sect. 6, we present computational
results. Conclusions are found in Sect. 7.
2. Block Asynchronous Iterative Algorithms
The asynchronous methods studied here for the solution
of (1) are based on the Block Jacobi algorithm, see, e.g., Varga [22].
Let the matrix A to be partitioned into 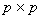 blocks
blocks
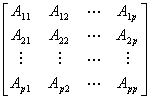 (3)
(3)
with the diagonal blocks 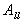 being square nonsingular of order
being square nonsingular of order 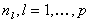 ,
, 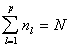 ,
and the vectors x and b are partitioned conformally.
,
and the vectors x and b are partitioned conformally.
ALGORITHM 1 (Block Jacobi). Given an initial approximation
of the vector
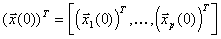
For t=1,2,…,until convergence For l=1 to
p, solve
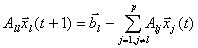 .
(4)
.
(4)
The entire linear system can be solved in parallel by
p processors, and the iteration vector at each step is
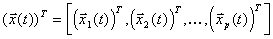 .
.
The solution of the system (4) is the block counterpart
to the iterations in (2). Thus as the discussion of Sect. 1 indicates,
this algorithm exchanges data for each value of t, and has at that
point a synchronization barrier. For the solution of each sub-system (4)
one can chose to use a different iterative method, such as Gauss-Seidel,
and this class of methods are called two-stage iterative methods; see e.g.,
[13,14], and the extensive references given therein.
For the asynchronous block Jacobi method, unlike in Algorithm
1, the processors are allowed to start the computation of the next iteration
of the block without waiting for the simultaneous completion of the same
iteration of other components. In other words, components of  are updated using a vector which is made of block components of previous,
not necessarily the latest, iterations. As in the standard references for
asynchronous algorithms, such as [6], the iteration subscript is increased
every time any (block) component of the iteration vector is computed. Thus,
one defines, the sets
are updated using a vector which is made of block components of previous,
not necessarily the latest, iterations. As in the standard references for
asynchronous algorithms, such as [6], the iteration subscript is increased
every time any (block) component of the iteration vector is computed. Thus,
one defines, the sets  by
by 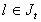 if the l-th block component of the iteration vector is computed
at the t-th step. Thus the Asynchronous Block Jacobi method can
be described as follows.
if the l-th block component of the iteration vector is computed
at the t-th step. Thus the Asynchronous Block Jacobi method can
be described as follows.
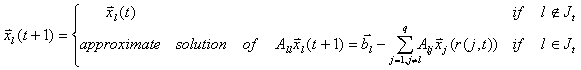 The term r(l,t) is used
to denote the iteration number of the l-th block-component being
used in the computation of any block-component in the t-th iteration,
i.e., the iteration number of the j-th block-component available
at the beginning of the computation of
The term r(l,t) is used
to denote the iteration number of the l-th block-component being
used in the computation of any block-component in the t-th iteration,
i.e., the iteration number of the j-th block-component available
at the beginning of the computation of 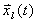 ,
if
,
if 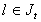 . We always assume that the terms r(l,t)
of our asynchronous iterative algorithms satisfy the following minimal
criteria as described in [14] and other references therein.
. We always assume that the terms r(l,t)
of our asynchronous iterative algorithms satisfy the following minimal
criteria as described in [14] and other references therein.
-
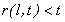 for all
for all 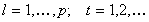
-
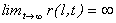 for all
for all 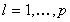
-
The set
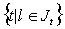 is unbounded for all
is unbounded for all 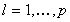 Convergence
of the Asynchronous Block Jacobi algorithm follows from results in [14];
see also [9].
Convergence
of the Asynchronous Block Jacobi algorithm follows from results in [14];
see also [9].
3. The Computational Test Problem
We use a magnetic field simulation problem as the test
case for it represents typical physical simulation applications and it
has a non-uniform geometry that requires load balancing when processed
in parallel. The processing environment is a cluster of shared 10 mbps
Ethernet connected DEC/Alpha workstations. Our simulation is to determine
the magnetic field in a region outside a permanent magnet [10]; i.e., solve
for 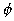 satisfying
satisfying
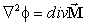 (5)
(5)
where 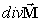 is the volume magnetic
charge density.
is the volume magnetic
charge density.
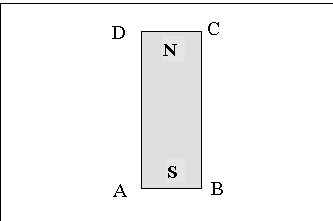 Figure 1: A Rectangular Magnet
For simplicity we chose to solve the two dimensional form
of the problem; see Fig. 1. The magnet is assumed to be uniformly magnetized,
i.e.,
Figure 1: A Rectangular Magnet
For simplicity we chose to solve the two dimensional form
of the problem; see Fig. 1. The magnet is assumed to be uniformly magnetized,
i.e., 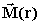 is a constant vector. Thus equation
(5) is reduced to the Laplacian everywhere except for the surface of the
magnet
is a constant vector. Thus equation
(5) is reduced to the Laplacian everywhere except for the surface of the
magnet
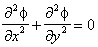 .
(6)
.
(6)
The rectangular domain in Fig. 1 is discretized using
an uniform grid with h horizontal and vertical spaces. Thus, the
grid points are labeled (i,j), i.j=1,2,3,...,n and we denote by
i,j the value of the function 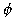 at the point of (i,j). The discretization of (6) using centered
differences is then
at the point of (i,j). The discretization of (6) using centered
differences is then
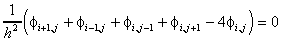 .
(7)
.
(7)
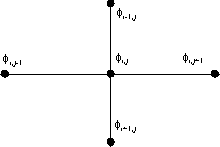 Figure 2: Grid around point (i,j)
Figure 2: Grid around point (i,j)
Therefore, the value of the magnetic field on each grid
point 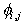 is a function of its four nearest
neighbors, see Fig. 2.
is a function of its four nearest
neighbors, see Fig. 2.
The Gauss-Seidel iteration scheme on equation (7) is
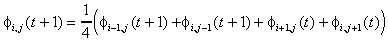 . (8)
. (8)
This means that for the calculation of 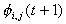 in each iteration cycle t, we use the most recent computed values
of that point's four first-neighbors. The boundaries of the rectangular
magnet have the following variations of (8) in order to incorporate the
discontinuities of
in each iteration cycle t, we use the most recent computed values
of that point's four first-neighbors. The boundaries of the rectangular
magnet have the following variations of (8) in order to incorporate the
discontinuities of 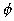 .
.
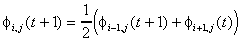 (Vertical edges)
(Vertical edges)
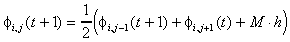 (Horizontal edges)
(Horizontal edges)
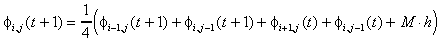 (Corners)
(Corners)
4. Parallel Algorithm Development
A parallel program is typically more complex than its
sequential counterpart. In this section, we first discuss our programming
tool choice. We then discuss our partitioning choices and introduce a number
of parallel implementation alternatives. Finally, we present an analysis
method that can be used to evaluate the parallel algorithms by capturing
the inherent interdependencies between the computing and communication
overheads.
4.1 Parallel Programming Tool
The choice of programming tool can have a large impact
on parallel implementation complexity and processing efficiency. An ideal
parallel processing environment for parallel asynchronous iterative algorithms
should be totally asynchronous with information over-write capabilities.
This is because for asynchronous parallel algorithms, the sender and receiver
are running independent of each other, and the receiver must obtain the
latest information or otherwise introduce artificial synchronization barriers;
see [20].
All message passing systems, such as MPI [19] and PVM
[5], use bounded buffers. This implies a synchronous semantics, namely
the sender should only send when the receiver is there to receive. Moreover,
the messages do not over-write each other. If we were to use any message
passing system, we had to implement the new messaging semantics on top
of the provided messaging channels. This would introduce much programming
complexity and processing overhead. Thus, we consider that these systems
are not appropriate for programming parallel asynchronous algorithms.
The Synergy system uses passive objects for parallel program
communication and synchronization. A passive object is coarse-grain data
structure with a set of pre-defined operators. An example passive object
is a tuple space with three operators: Read, Put and Get.
The semantics of these operators is similar to rd, get and
put operations in the Linda system [1] provided that tuples are
uniquely named and First-In-First-Out (FIFO) ordered. Writing to the same
named tuple means over-writing the existing tuple's content. This characteristic
ideally meets the asynchronous iterative algorithm's requirement. The object
passiveness restricts the operators from dynamically creating new objects
at runtime. They can only create instances within an object thus leaving
the outset communication topology fixed for each application. This feature
was designed to facilitate automatic generation of efficient client/server
programs from a fixed application configuration topology. For a more detailed
description of Synergy, we refer the reader to [8].
Passive objects embed multithreaded controls under a simple
asynchronous programming interface. Thus, there is no explicit process
manipulation and synchronization statements in either the sender or the
receiver programs. Unless specifically coded, each individual program has
a single thread control within its programming space.
4.2 Data Partition Choice
A typical parallel implementation of a block iterative
algorithm, such as Block Gauss-Seidel [6,16], assigns several mesh points
to each processor such that each processor only communicates with its four
nearest neighbors; see Fig. 3, where there are p=9 processors and
n=36.
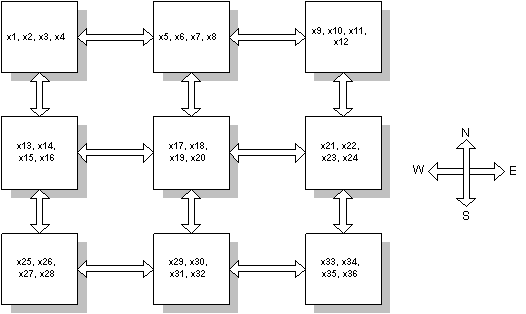 Figure 3: Typical parallel block-matrix operations
Figure 3: Typical parallel block-matrix operations
This intuitive parallel implementation, called tiles,
has the following drawbacks:
-
In comparison with partitioning in stripes, the tile
partitioning requires less overall inter-processor communication data volume
but more communication sessions at each iteration due to more interfaces
with the neighbors. Since establishing a communication session between
processes needs more time than moving a few thousand bytes of data on a
typical interconnection network hardware, for many practical problems the
tile partitioning is guaranteed to deliver poor performance when compared
to striping. This conclusion was recorded in studies comparing striping,
tiling and penciled partitions on clusters of workstations [11], the IBM
SP2, iPSC/860 and Cray T3D processors [17].
-
Low calculation amount per data exchange due to the small
grain size. This also causes low efficiency.
-
Pipelined processors with short data streams are not effective
in saving time.
A parallel implementation is more effective if we can increase
the calculation amount per data exchange, reduce the synchronization frequency
and decrease the communication sessions. Therefore, in this paper, we focus
on developing striped block asynchronous algorithms; see Fig. 4.
 Figure 4: Row block decomposition
We abuse the notation and say that
Figure 4: Row block decomposition
We abuse the notation and say that 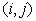 q implying that the grid point
q implying that the grid point 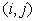 is
in the block of variables assigned to processor q
is
in the block of variables assigned to processor q 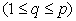 .
.
Each grid point on the simulation mesh requires the values
of its first neighbors during iteration t, as seen in (8). If we
divide the rectangular grid of points into blocks of rows, with each block
considered one work assignment and this block of rows corresponds
to a diagonal block 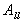 of the matrix A
in (1), as shown in (3). Therefore, in Fig. 4, only the top and bottom
rows of each block needs to be exchanged between neighboring processors.
of the matrix A
in (1), as shown in (3). Therefore, in Fig. 4, only the top and bottom
rows of each block needs to be exchanged between neighboring processors.
4.3 Stopping Criteria
One way to look at the block asynchronous algorithm is
to think of it as a relaxation from the point algorithm (2). In other words,
we reduce the inter-process communications by transmitting the most
recent approximations only after each processor has performed a specified
amount of calculations (inner iterations). We define this amount
of calculations as the dataflow reduction criterion (DRC), i.e.,
stopping criteria in the approximation process. An inter-processor information
exchange is called an outer iteration.
There are two distinct ways of defining DRC: one by measuring
the size of the inner residuals; and another by setting a fixed number
of inner iteration limit. For the first case, let us define the residual
computed in the processor q as
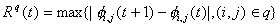 .
.
This quantity is kept in the processor's memory between
successive iterations, and it is checked if the residual is reduced by
a specific amount. We use a threshold 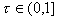 and
we say that the residual threshold criterion is met, when the residual
is reduced by a factor of
and
we say that the residual threshold criterion is met, when the residual
is reduced by a factor of 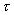 , i.e., when
, i.e., when 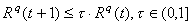 .
.
4.4 Load Balancing and Block Allocation Methods
The overall processing of the parallel program is as follows.
A master process partitions the matrix into work assignments and distributes
them to parallel workers. A worker process starts calculations after it
receives a work assignment and some global information. It starts information
exchange with its neighbors when the DRC is satisfied. Since multiple copies
of the same worker code run simultaneously, it is easy to imagine that
workers will exchange data with their neighbors at different times.
After a worker receives values of the border elements
from its neighbors, it will resume the same calculation process until the
next DRC is met. A block is considered solved locally when the residual
of the block q falls below a prescribed e,
i.e., when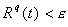 . The master process then collects
all solved blocks and performs a Gauss-Seidel iteration across the reconstructed
linear system to check if the local solutions are indeed globally convergent.
The system terminates if a global convergence is reached. Otherwise the
master re-partitions the system and re-transmits the blocks. The re-calculation
cycles can generate very large communication volume. A system becomes unstable
when the number of re-calculations is too large. An unstable system indicates
that the processors are diverging into local solutions.
. The master process then collects
all solved blocks and performs a Gauss-Seidel iteration across the reconstructed
linear system to check if the local solutions are indeed globally convergent.
The system terminates if a global convergence is reached. Otherwise the
master re-partitions the system and re-transmits the blocks. The re-calculation
cycles can generate very large communication volume. A system becomes unstable
when the number of re-calculations is too large. An unstable system indicates
that the processors are diverging into local solutions.
To further reduce the communication we can restrict the
number of workers and put an exact amount of rows on each (static partition).
This strategy can cause work load imbalance thus negatively impact our
performance since our computational test problem is a magnet with non-uniform
geometry. To ease the load imbalance, we can put many smaller blocks (dynamic
partitioning) in an FIFO queue having the processors fetch the block assignments
when they become idle. This way computing-intensive blocks will be automatically
processed more often. The drawback is that it requires more network traffic.
4.4.1 Static Allocation Algorithm Details
A static parallel block iterative algorithm has a master
and many workers. The master program is responsible for constructing the
n n grid geometry, partitioning the grid into blocks of rows, assigning
these blocks to the p worker modules residing on different processors,
receiving results, and composing the solution matrix. Each row block that
is assigned to a worker module is composed of n/p rows.
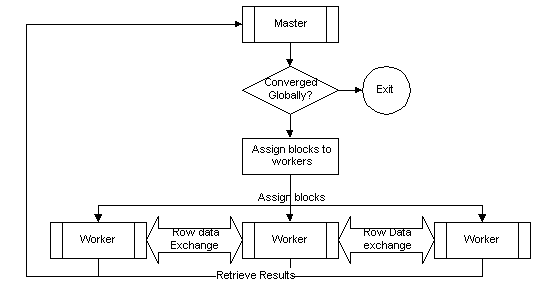
Figure 5: Static block allocation method
A worker module q performs Gauss-Seidel iterations
on the grid points of the assigned block which is composed of rows with
indexes between 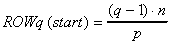 and
and 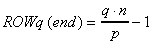 ,
until it meets the DRC. At this point it will transmit to their neighbors
values of the grid points on their border rows, and receive from them the
updated values from the neighbors. In particular, worker q will
transmit
,
until it meets the DRC. At this point it will transmit to their neighbors
values of the grid points on their border rows, and receive from them the
updated values from the neighbors. In particular, worker q will
transmit
-
To its upper neighbor (worker q-1),
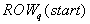 and receive from it
and receive from it 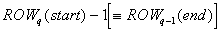
-
To its lower neighbor (worker q+1),
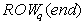 and receive from it
and receive from it 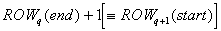 In both cases, if the
neighboring workers have not reached the threshold control criteria yet,
worker q is going to use values received from its neighbors in a
previous outer iteration. The worker will repeat the above procedure, until
the local convergence criterion is met. At that point it will return all
its approximated grid point values to the master module.
In both cases, if the
neighboring workers have not reached the threshold control criteria yet,
worker q is going to use values received from its neighbors in a
previous outer iteration. The worker will repeat the above procedure, until
the local convergence criterion is met. At that point it will return all
its approximated grid point values to the master module.
After receiving all locally converged blocks from the workers,
the master module checks if the global convergence criterion 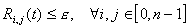 ,
where
,
where 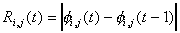 .
.
If not, then it reassigns the blocks to the p workers.
This procedure is repeated until the global convergence criterion is met.
4.4.2 Dynamic Allocation Algorithm Details
In this variation of the block-asynchronous parallel algorithm,
only the worker module is modified, so that it uses the tuple space as
the working assignment queue. As in the static version, a working assignment
(a row-block partition of the grid) is a tuple. The tuple space is used
as a FIFO queue containing all non-convergent tuples that have met the
given DRC.
A dynamic worker module first reads global data (problem
geometry) from the tuple space. It then extracts a work assignment tuple
to compute. After the DRC is met, it will insert its border rows to be
used by neighboring partitions. If local convergence is reached, it inserts
the result for the master to retrieve. Otherwise, it reinserts the work
assignment into the working tuple space. Such reinsertion will place the
tuple at the end of the FIFO queue (see Fig. 6). If the number of working
tuples is greater than the number of processors, a slow converging region
will be processed by multiple processors. This can reduce load imbalance.
5. Parallel Program Evaluation
In this section, we build timing models for the static
and dynamic partitioning algorithms. The objective is to identify the relative
merits of both algorithms judging from their inherent interdependencies
between the parallel computation and communication times. Note that the
performance difference between inner iteration limit control and residual
threshold control cannot be modeled analytically but can be observed via
computational results.
Timing models [21] are program time complexity-based models.
Timing analysis requires timing models for the sequential algorithm and
the corresponding parallel algorithm. Our scalability analysis requires
calibrating the processing parameters by running once the sequential and
parallel programs on a target environment.
We use the following symbols in the timing model analysis.N
Number of grid points (= n n)Qc Number of floating point
operations required per grid pointQN Number of bytes
required per grid pointI Number of inner iterationsE Number
of outer iterationsW Processor power in number of algorithmic steps
per secondu Network capacity in number of bytes per secondNote that
W=W'/c represents the delivered processing power in number of algorithmic
steps (as related to their time complexity models) per second, where W'
is the actual processor power in number of machine instructions per second
and c is a constant reflecting the average number of machine instructions
generated from each algorithmic step. For our computational test problem,
Qc= 11.
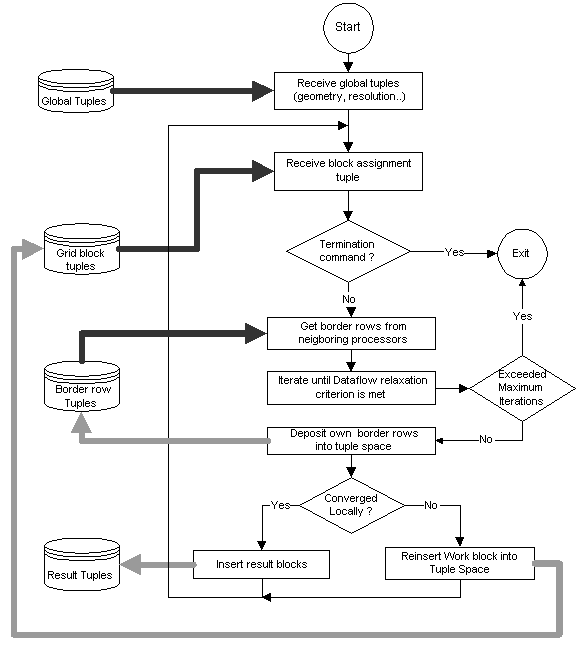 Figure 6: Dynamic blockallocation - Worker module
Figure 6: Dynamic blockallocation - Worker module
5.1 Sequential Gauss-Seidel Model
The sequential processing time can be modeled as
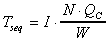 .
(9)
.
(9)
To calibrate W, we run the sequential algorithm
on two different processors: Intel486/100 MHZ and DEC Alpha/120 MHz. Here
is a summary of the statistics.
|
Resolution (n n)
|
3232
|
6464
|
128128
|
256256
|
|
Iterations (I)
|
612
|
2258
|
8812
|
31790
|
|
Intel 486 time (sec)
|
4.7
|
67.8
|
1179.3
|
16810.2
|
|
DEC Alpha time (sec)
|
3.0
|
42.4
|
789.3
|
11742.8
|
Using (9) and the above table, we can derive the graph in Fig. 7 depicting
W , in million steps per second (Msps), as a function of the problem
size N (grid resolution).
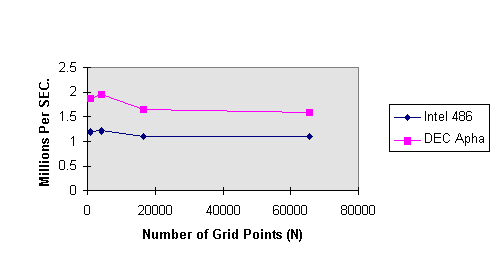 Figure 7. W as a Function of N
Figure 7. W as a Function of N
From Fig. 7 we can readily observe that there are little swapping effects.
All programs can fit into memory. We can also notice the presence of a
large constant c for this algorithm in comparison to other well
known algorithms such as matrix multiplication and Linpack (see table below).
|
Linpack |
Matrix Multiply (200200) |
| Intel486/100MHz/8MB |
2.4 Msps |
4.3 Msps |
| Alpha/120MHz/32MB |
6.4 Msps |
29.4 Msps |
5.2 Static Block Allocation Algorithm
Parallel iterative algorithms can be modeled as a compute-aggregate-broadcast
system as shown in Fig. 8.
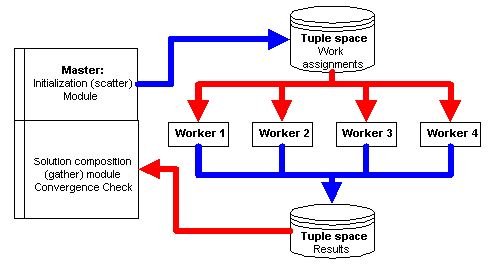 Figure 8. Compute-Aggregate-Broadcast (CAB)
Figure 8. Compute-Aggregate-Broadcast (CAB)
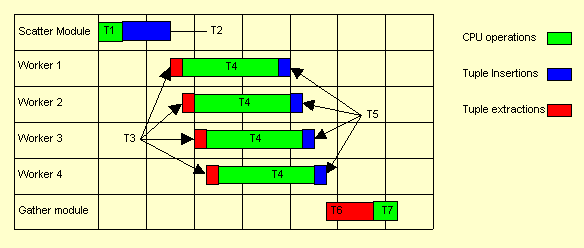 Figure 9. CAB Timing Profile
This type systems have a typical timing profile as shown
in Fig. 9, where T1 is the Master initialization time, T2 is the task (tuple)
distribution time, T3 is the Worker tuple extraction time, T4 is the Worker
local solution computing time, T5 is the Worker result submission time,
T6 is the Master result tuple extraction time, and T7 is the Master sanity
checking. The program may re-iterate T2-T7 if global convergence check
fails. Otherwise, it terminates. Note that for parallel processors using
shared-medium networks or buses, communication times T2 and T3 do not overlap,
nor do T5 and T6.
Figure 9. CAB Timing Profile
This type systems have a typical timing profile as shown
in Fig. 9, where T1 is the Master initialization time, T2 is the task (tuple)
distribution time, T3 is the Worker tuple extraction time, T4 is the Worker
local solution computing time, T5 is the Worker result submission time,
T6 is the Master result tuple extraction time, and T7 is the Master sanity
checking. The program may re-iterate T2-T7 if global convergence check
fails. Otherwise, it terminates. Note that for parallel processors using
shared-medium networks or buses, communication times T2 and T3 do not overlap,
nor do T5 and T6.
To simplify the analysis, we express the total parallel
processing time as
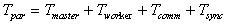 ,
(10)
,
(10)
where 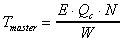 which defines
Master's total pure computation time,
which defines
Master's total pure computation time, 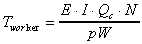 which defines the maximum worker pure computation time (among p
parallel workers), and
which defines the maximum worker pure computation time (among p
parallel workers), and
 . (11)In (11),
. (11)In (11), 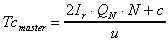 which defines the master's total communication time including broadcast
of global geometry, distribution of working tuples and extraction of result
tuples, and
which defines the master's total communication time including broadcast
of global geometry, distribution of working tuples and extraction of result
tuples, and 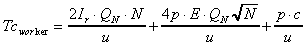 which defines the total worker's
communication time including extraction of global information, extraction
of working tuples, return of result tuples and intermediate exchange of
data with neighboring processors. Lastly,
which defines the total worker's
communication time including extraction of global information, extraction
of working tuples, return of result tuples and intermediate exchange of
data with neighboring processors. Lastly, 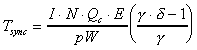 which defines the worst-case load imbalancing overhead assuming
which defines the worst-case load imbalancing overhead assuming 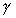 times difference between the fastest and slowest processors and
times difference between the fastest and slowest processors and 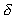 times differences between the fastest converging block and the slowest
converging block.
times differences between the fastest converging block and the slowest
converging block.
Finally, we can define the static block algorithm timing
to be
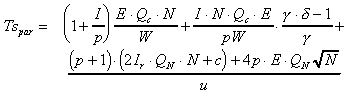 (12)
(12)
5.3 Dynamic Block Allocation Algorithm
The dynamic block allocation algorithm has a similar model except that
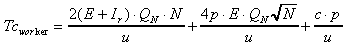 .
.
Here, assuming the best load balancing (Tsync = 0), the only difference
in the is in the tuple re-insertion overhead. Therefore, the total dynamic
time model is
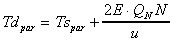 .
(13)
.
(13)
An important investigation is to quantitatively decide when to use static
and when to use dynamic block allocation algorithm in terms of parallel
processing environments and problem sizes. Figs. 10 and 11 are obtained
with numerical calculations using (12) , (13) and the following assumptions:
N = 256 256
W = 2.5 Mflops (million algorithmic steps per second)
u = 100 K Bytes Per Second
c = 100 K bytes (Global broadcast data size)
Qc = 11 Operations per grid point
QN = 8 bytes per grid point
p = 5
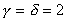 (two times difference in load imbalance).
(two times difference in load imbalance).
Fig. 10 illustrates that for the given parallel processing
environment, only the static algorithm will out-perform the sequential
one. However, static algorithm's convergence time will increase more rapidly
than the dynamic algorithm as we increase local iterations to reduce communication.
Fig. 11 indicates that when the network speed goes above a certain point
(approximately sustained 600 KBPS), the dynamic algorithm will out-perform
the static algorithm.
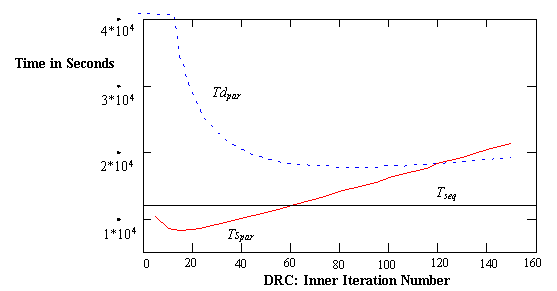 Figure 10. Static vs. Dynamic with Respect to Inner Iteration
Control (I)
Figure 10. Static vs. Dynamic with Respect to Inner Iteration
Control (I)
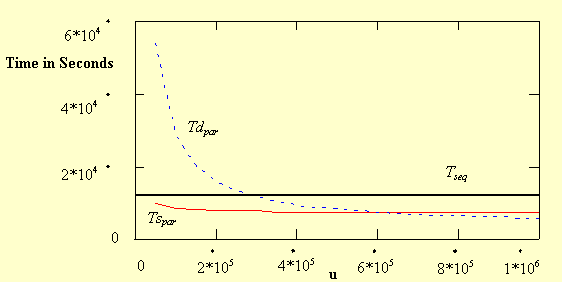 Figure 11. Static vs. Dynamic with Respect to Network Speed
(u)
Figure 11. Static vs. Dynamic with Respect to Network Speed
(u)
6. Computational Results
Our computational results validate the predictions of
the timing models, e.g., the shape of the curve Tdpar
in Fig. 10 is confirmed in Fig. 13(a), and that of Tspar
in Fig. 10 is confirmed in Fig. 15(a). The experiments reveal the quantitative
performance consequences of data exchange frequencies and compare residual
and inner iteration control methods. We have produced four sets of experiments.
These are dynamic block allocation with residual threshold control,
dynamic block allocation with inner iteration control, static
block allocation with residual threshold control, and static block
allocation with inner iteration control. The parallel processing environment
is a cluster of five (5) DEC/Alpha workstations running the OSF/1 operating
system. The workstations use a shared 10 mbps Ethernet. The parallel programming
environment is C and Synergy V3.0 system.
For each set of experiments, we report elapsed times,
total outer iterations and the number of total iterations.
Elapsed time measures the actual wall-clock time of the application. Total
outer iteration records the changes in outer iteration by the respective
iteration control methods. Total iteration records the changes in maximal
number of inner iterations performed by a parallel worker process. The
problem size is 256256 grid points (or N = 65,536 equations). Parallel
processing will yield no advantage for problems of smaller sizes.
From the performance charts (Figs. 12-15), we observe the following:
-
The elapsed time curves of inner iteration control of both
dynamic and static allocations obey the timing model predictions, compare
Fig. 10 Tdpar and Tspar curves
with Figs. 13(a) and 15(a). Considering that the timing models have ignored
some dynamic details, the predicted optimal static DRC is very close to
computational results. The predicted DRCs are 17 (Tspar)
and 80 (Tdpar) respectively (Fig. 10). The actual static
and dynamic optimal DRCs are 19 (Fig. 15(a)) and 30 (Fig. 13(a)).
-
The total iteration increases linearly as we cut-off the
data exchanges, see Figs. 12(c) - 15(c).
-
Using the 11,742.8 second sequential elapsed time (see Sect.
5.1) as comparison we have the following results. Dynamic allocation with
threshold control finishes in 8,551.35 seconds,
or speedup=1.37 (see Fig. 12(a)). Dynamic allocation with iteration control
finished in 6,756.39 seconds, or speedup=1.74 (see
Fig. 13(a)). Static block algorithms performed
better. Static threshold control finished in 5,746.01
seconds, or speedup=2.04 (see Fig. 14(a)). Static allocation with iteration
control finished in 3,577.92 seconds, or speedup=3.28 (Fig. 15(a)). The
best speedup represents 66% parallel processing efficiency using five processors.
Residual threshold control is consistently slower than inner
iteration control.
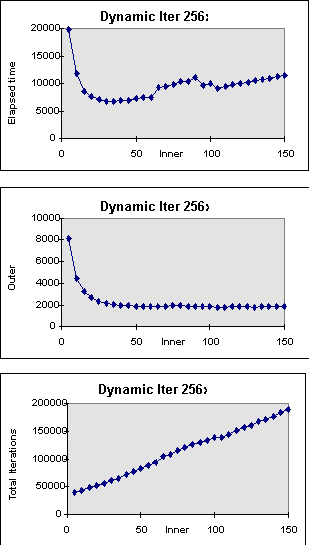 Figure 12. Dynamic Block Allocation with Inner Iteration Control
Figure 12. Dynamic Block Allocation with Inner Iteration Control
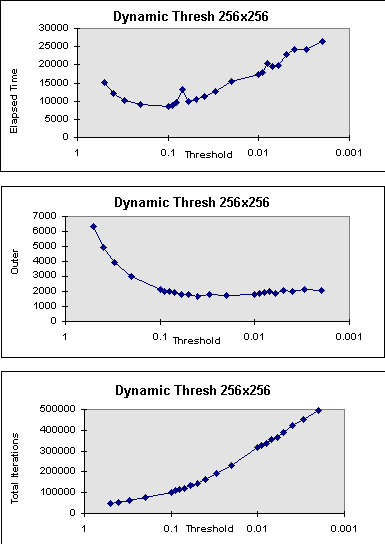 Figure 13. Dynamic Block Allocation with Residual Threshold
Control
Figure 13. Dynamic Block Allocation with Residual Threshold
Control
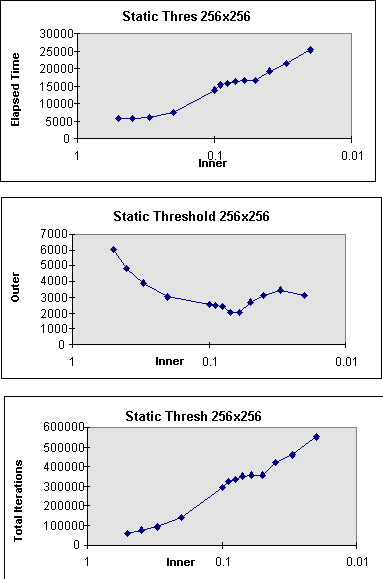 Figure 14. Static Block Allocation with Residual Threshold Control
Figure 14. Static Block Allocation with Residual Threshold Control
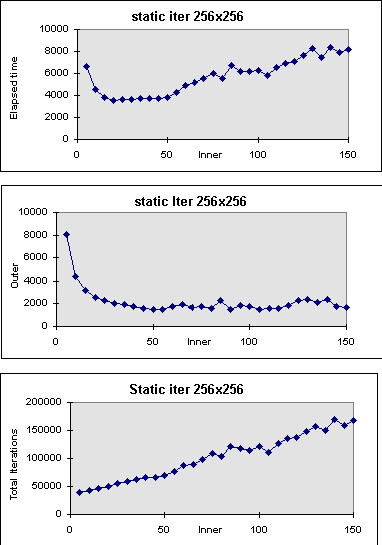
Figure 15. Static Block Allocation with Inner Iteration Control
7. Conclusions
In this paper we report our analysis and computational
results of an investigation that trades the abundance of computing power
for scarce network bandwidth using asynchronous iterative algorithms. We
consider that message-passing parallel systems are inappropriate for asynchronous
parallel programs.
Our results show that it is possible to gain overall processing
speed by sacrificing some local convergence speed. We have also found that
the convergence time increases linearly (see Sect. 6) as we reduce data
exchange frequency. Since overall cumulative speed of multiple processors
is typically many times of the interconnection network speed, for most
practical applications asynchronous iterative algorithms are more advantageous
than synchronous algorithms when processed in parallel.
Our experiences in applying the timing model method to
parallel algorithm analysis showed that it is possible to analytically
prototype a complex parallel system with little program instrumentation.
The results can be used to predict the scalability of the system as well
as optimal control points.
References
-
S. Ahuja, N. Carriero and D. Gelertner, Linda and friends,
IEEE Computer, 26-32, August 1986.
-
G.S. Almasi, and A. Gotlieb, Highly Parallel Computing. The
Benjamin-Cummings Publishing Co. New York, 1989.
-
N. S. Asaithambi, Numerical Analysis, Saunders College
Publishing, Philadelphia, 1995.
-
D. Bailey, Twelve Ways to Fool the Masses When Giving Performance
Results on Parallel Computers. RNR Technical Report, RNR-091-020, NASA
Ames Research Center, 1991.
-
A. Beguelin, J. Dongarra, A. Geist R. Mancheck and V. Sunderam.
PVM: Heterogeneous Network Computing. Sixth SIAM Conference on Parallel
Processing. SIAM, 1993.
-
D. P. Bertsekas and J. N. Tsitsiklis. Parallel and Distributed
Computation. Prentice Hall, Englewood Cliffs, New Jersey, 1989.
-
K. Blathras. A systematic dataflow relaxation method for
computationally intense iterative algorithms, Dissertation proposal,
CIS Temple University, Philadelphia, 1995.
-
K. Blathras, J. Dougherty and Y. Shi. The Synergy system:
Tools for computing the future, Supercomputing '92, Minneapolis,
1992.
-
R. Bru, V. Migallon, J. Penades and D. B. Szyld. Parallel,
synchronous and asynchronous two-stage multisplitting methods. Electronic
Transactions on Numerical Analysis, 3:24-38, 1995.
-
M. I. Darby, Calculation of the fields near permanent magnets,
Physics Programs, 125-149, John Wiley & Sons, New York, 1980.
-
J. Dougherty, Variable-Size Partitioning Approaches for a
Distributed Application, Joint Conference on Information Sciences, Pinehurst,
N.C., November, 1994.
-
K. Dowd, High Performance computing, O'Reilly &
Associates, Sebastopol, CA, 1993
-
A. Frommer and D. B. Szyld. H-splittings and two-stage iterative
methods. Numerische Mathematik, 63:345-356, 1992.
-
A. Frommer and D. B. Szyld. Asynchronous two-stage iterative
methods. Numerische Mathematik, 69:141-153, 1994.
-
F. Halsal, Data Communications, Computer Networks and
Open Systems, Addison-Wesley, New York, 1996.
-
D. P. Koester, S. Ranka, and G. C. Fox, A Parallel Gauss-Seidel
Algorithm for Sparse power system matrices, Proceedings of Supercomputing
'94, 184-193, 1994.
-
S. Kortas and P. Angot, A Practical and Portable Model for
Programming for Iterative Solvers on Distributed Memory Machines, Parallel
Computing, 22, 1996, pp487-512.
-
P. J. Lanzkron, D. J. Rose and D. B. Szyld, Numerische Mathematik,
58:685-702, 1991.
-
Message passing Interface Forum. MPI: A message passing interface
standard. CIS Technical report CS-94-230, University of Tennessee,
Knoxville, 1994
-
D. A. Reed and R.M. Fujimoto. Message Based Parallel Processing,
The MIT Press, Boston, 1988.
-
Y. Shi. Timing Models: Towards the scalability analysis of
parallel programs, CIS Tech. Report, Temple University, Philadelphia,
1994.
-
R. S. Varga. Matrix Iterative Analysis, Prentice Hall,
Englewood Cliffs, New Jersey 1962.
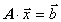 ,
(1)
,
(1)
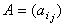 is a large
is a large 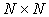 matrix, and x and b are N-vectors. This problem lies
at the core of many scientific and engineering applications. The computational
test problem we use in this paper is that of the determination of the magnetic
field in a region outside of a permanent magnet [10]; see further Sect.
3. Since full direct methods for the solution of (1) require
matrix, and x and b are N-vectors. This problem lies
at the core of many scientific and engineering applications. The computational
test problem we use in this paper is that of the determination of the magnetic
field in a region outside of a permanent magnet [10]; see further Sect.
3. Since full direct methods for the solution of (1) require 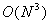 operations and usually sparse methods lack parallelism, we concentrate
in this paper on iterative methods, which are used in practice due to their
reduced time complexity.
operations and usually sparse methods lack parallelism, we concentrate
in this paper on iterative methods, which are used in practice due to their
reduced time complexity.
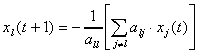 , l=1,2,…N; t=0,1, …;
(2)
, l=1,2,…N; t=0,1, …;
(2)
 If each of p processors
compute one of the components of x in (2), i.e., p=N, this
implies a very large amount of data "shuffling" between processors at each
iteration. Furthermore, all processors must synchronize at that point creating
a time barrier.
If each of p processors
compute one of the components of x in (2), i.e., p=N, this
implies a very large amount of data "shuffling" between processors at each
iteration. Furthermore, all processors must synchronize at that point creating
a time barrier.
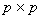 blocks
blocks
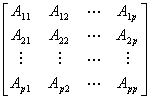 (3)
(3)
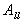 being square nonsingular of order
being square nonsingular of order 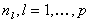 ,
, 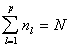 ,
and the vectors x and b are partitioned conformally.
,
and the vectors x and b are partitioned conformally.
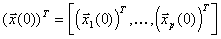
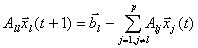 .
(4)
.
(4)
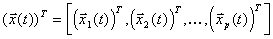 .
.
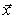 are updated using a vector which is made of block components of previous,
not necessarily the latest, iterations. As in the standard references for
asynchronous algorithms, such as [6], the iteration subscript is increased
every time any (block) component of the iteration vector is computed. Thus,
one defines, the sets
are updated using a vector which is made of block components of previous,
not necessarily the latest, iterations. As in the standard references for
asynchronous algorithms, such as [6], the iteration subscript is increased
every time any (block) component of the iteration vector is computed. Thus,
one defines, the sets 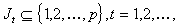 by
by 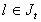 if the l-th block component of the iteration vector is computed
at the t-th step. Thus the Asynchronous Block Jacobi method can
be described as follows.
if the l-th block component of the iteration vector is computed
at the t-th step. Thus the Asynchronous Block Jacobi method can
be described as follows.
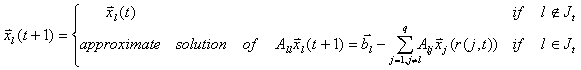 The term r(l,t) is used
to denote the iteration number of the l-th block-component being
used in the computation of any block-component in the t-th iteration,
i.e., the iteration number of the j-th block-component available
at the beginning of the computation of
The term r(l,t) is used
to denote the iteration number of the l-th block-component being
used in the computation of any block-component in the t-th iteration,
i.e., the iteration number of the j-th block-component available
at the beginning of the computation of 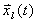 ,
if
,
if 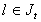 . We always assume that the terms r(l,t)
of our asynchronous iterative algorithms satisfy the following minimal
criteria as described in [14] and other references therein.
. We always assume that the terms r(l,t)
of our asynchronous iterative algorithms satisfy the following minimal
criteria as described in [14] and other references therein.
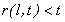 for all
for all 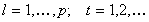
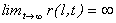 for all
for all 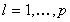
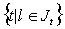 is unbounded for all
is unbounded for all 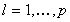 Convergence
of the Asynchronous Block Jacobi algorithm follows from results in [14];
see also [9].
Convergence
of the Asynchronous Block Jacobi algorithm follows from results in [14];
see also [9].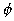 satisfying
satisfying
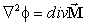 (5)
(5)
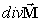 is the volume magnetic
charge density.
is the volume magnetic
charge density.

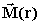 is a constant vector. Thus equation
(5) is reduced to the Laplacian everywhere except for the surface of the
magnet
is a constant vector. Thus equation
(5) is reduced to the Laplacian everywhere except for the surface of the
magnet
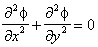 .
(6)
.
(6)
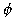 at the point of (i,j). The discretization of (6) using centered
differences is then
at the point of (i,j). The discretization of (6) using centered
differences is then
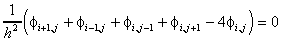 .
(7)
.
(7)
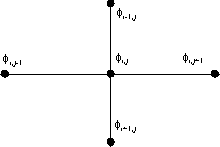
 is a function of its four nearest
neighbors, see Fig. 2.
is a function of its four nearest
neighbors, see Fig. 2.
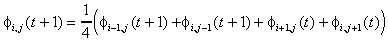 . (8)
. (8)
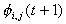 in each iteration cycle t, we use the most recent computed values
of that point's four first-neighbors. The boundaries of the rectangular
magnet have the following variations of (8) in order to incorporate the
discontinuities of
in each iteration cycle t, we use the most recent computed values
of that point's four first-neighbors. The boundaries of the rectangular
magnet have the following variations of (8) in order to incorporate the
discontinuities of 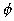 .
.
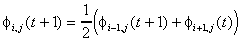 (Vertical edges)
(Vertical edges)
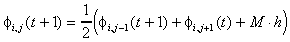 (Horizontal edges)
(Horizontal edges)
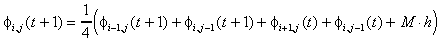 (Corners)
(Corners)


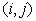 q implying that the grid point
q implying that the grid point 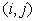 is
in the block of variables assigned to processor q
is
in the block of variables assigned to processor q 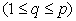 .
.
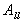 of the matrix A
in (1), as shown in (3). Therefore, in Fig. 4, only the top and bottom
rows of each block needs to be exchanged between neighboring processors.
of the matrix A
in (1), as shown in (3). Therefore, in Fig. 4, only the top and bottom
rows of each block needs to be exchanged between neighboring processors.
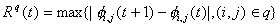 .
.
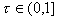 and
we say that the residual threshold criterion is met, when the residual
is reduced by a factor of
and
we say that the residual threshold criterion is met, when the residual
is reduced by a factor of  , i.e., when
, i.e., when 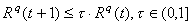 .
.
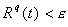 . The master process then collects
all solved blocks and performs a Gauss-Seidel iteration across the reconstructed
linear system to check if the local solutions are indeed globally convergent.
The system terminates if a global convergence is reached. Otherwise the
master re-partitions the system and re-transmits the blocks. The re-calculation
cycles can generate very large communication volume. A system becomes unstable
when the number of re-calculations is too large. An unstable system indicates
that the processors are diverging into local solutions.
. The master process then collects
all solved blocks and performs a Gauss-Seidel iteration across the reconstructed
linear system to check if the local solutions are indeed globally convergent.
The system terminates if a global convergence is reached. Otherwise the
master re-partitions the system and re-transmits the blocks. The re-calculation
cycles can generate very large communication volume. A system becomes unstable
when the number of re-calculations is too large. An unstable system indicates
that the processors are diverging into local solutions.

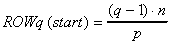 and
and 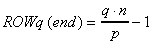 ,
until it meets the DRC. At this point it will transmit to their neighbors
values of the grid points on their border rows, and receive from them the
updated values from the neighbors. In particular, worker q will
transmit
,
until it meets the DRC. At this point it will transmit to their neighbors
values of the grid points on their border rows, and receive from them the
updated values from the neighbors. In particular, worker q will
transmit
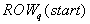 and receive from it
and receive from it 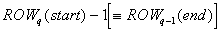
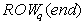 and receive from it
and receive from it 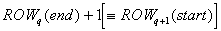 In both cases, if the
neighboring workers have not reached the threshold control criteria yet,
worker q is going to use values received from its neighbors in a
previous outer iteration. The worker will repeat the above procedure, until
the local convergence criterion is met. At that point it will return all
its approximated grid point values to the master module.
In both cases, if the
neighboring workers have not reached the threshold control criteria yet,
worker q is going to use values received from its neighbors in a
previous outer iteration. The worker will repeat the above procedure, until
the local convergence criterion is met. At that point it will return all
its approximated grid point values to the master module.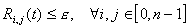 ,
where
,
where 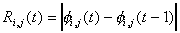 .
.

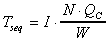 .
(9)
.
(9)



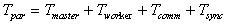 ,
(10)
,
(10)
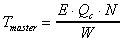 which defines
Master's total pure computation time,
which defines
Master's total pure computation time, 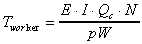 which defines the maximum worker pure computation time (among p
parallel workers), and
which defines the maximum worker pure computation time (among p
parallel workers), and
 . (11)In (11),
. (11)In (11), 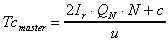 which defines the master's total communication time including broadcast
of global geometry, distribution of working tuples and extraction of result
tuples, and
which defines the master's total communication time including broadcast
of global geometry, distribution of working tuples and extraction of result
tuples, and 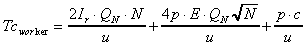 which defines the total worker's
communication time including extraction of global information, extraction
of working tuples, return of result tuples and intermediate exchange of
data with neighboring processors. Lastly,
which defines the total worker's
communication time including extraction of global information, extraction
of working tuples, return of result tuples and intermediate exchange of
data with neighboring processors. Lastly, 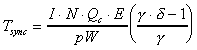 which defines the worst-case load imbalancing overhead assuming
which defines the worst-case load imbalancing overhead assuming 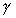 times difference between the fastest and slowest processors and
times difference between the fastest and slowest processors and 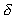 times differences between the fastest converging block and the slowest
converging block.
times differences between the fastest converging block and the slowest
converging block.
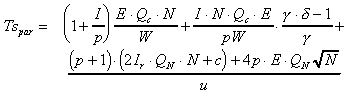 (12)
(12)
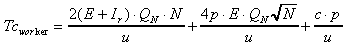 .
.
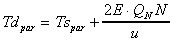 .
(13)
.
(13)
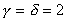 (two times difference in load imbalance).
(two times difference in load imbalance).





