Yuan Shi
Computer and Information Sciences Department
Room 305
Temple University (MS:38-24)
Philadelphia, PA 19122
shi@falcon.cis.temple.edu
215/204-6437(Voice) 215/204-5082(Fax)
October 1996
Researchers in the parallel processing community have been using Amdahl's
Law and Gustafson's Law to obtain estimated speedups as measures of parallel
program potential. In 1967, Amdahl's Law was used as an argument against
massively parallel processing. Since 1988 Gustafson's Law has been used
to justify massively parallel processing (MPP). Interestingly, a careful
analysis reveals that these two laws are in fact identical. The
well publicized arguments were resulted from misunderstandings of the nature
of both laws.
This paper establishes the mathematical equivalence between Amdahl's
Law and Gustafson's Law. We also focus on an often neglected prerequisite
to applying the Amdahl's Law: the serial and parallel programs must compute
the same total number of steps for the same input. There is a class of
commonly used algorithms for which this prerequisite is hard to satisfy.
For these algorithms, the law can be abused. A simple rule is provided
to identify these algorithms.
We conclude that the use of the "serial percentage" concept
in parallel performance evaluation is misleading. It has caused nearly
three decades of confusion in the parallel processing community. This confusion
disappears when processing times are used in the formulations. Therefore,
we suggest that time-based formulations would be the most appropriate for
parallel performance evaluation.
This page is intentionally left blank to confirm with the JIDP's typesetting requirement.
1. Introduction
In parallel program evaluation Amdahl's Law has been widely cited. The
analytical formulations in the literature, however, have caused much confusion
to the understanding of the nature of the law [2]. The best known misuse
was perhaps the argument against massively parallel processing (MPP) [1].
The key to Amdahl's Law is a serial processing percentage relative to
the overall program execution time using a single processor. Therefore
it is independent of the number of processors. It is then possible
to derive an upper bound of speedup when the number of processors (P)
approaches infinity. It seemed that small serial percentages, such as 0.01-0.05,
can restrict speedup to very small values. This observation had spread
much pessimism in the parallel processing community. Parallel computational
experiments indicate that many practical applications have indeed very
small serial percentages, much smaller than we had imagined.
Gustafson revealed that it was indeed possible to achieve more than
1000 fold speedup using 1024 processors [4]. This appeared to have "broken"
the Amdahl's Law and to have justified massively parallel processing.
An alternative formulation was proposed. This is often referred to as
the Gustafson's Law [5] and has been widely refereed to as a "scaled
speedup measure". In Gustafson's formulation, a new serial percentage
is defined in reference to the overall processing time using P processors.
Therefore it is dependent on P. This P dependent serial
percentage is easier to obtain than that in Amdahl's formulation via computational
experiments. But mathematically, Gustafson's formulation cannot
be directly used to observe P's impact on speedup since it contains
a P dependent variable.
Unfortunately, many people have mistakenly considered the two serial
percentages are identical. Gustafson's original paper contains the same
error in claiming finding an exception to the Amdahl's Law..
A careful analysis reveals that these two serial percentages are directly
related by a simple equation. Translating the P dependent serial
percentage in Gustafson's formulation to P independent serial percentage
yields an identical formula as Amdahl's. This means that there is
really only one law but two different formulations. Much
of the publicized arguments were indeed misunderstandings resulted from
this confusion.
Another point often neglected is the prerequisite to applying Amdahl's Law. It requires the serial algorithm to retain its structure such that the same number of instructions are processed by both the serial and the parallel implementations for the same input. Often the parallel implementation is directly crafted from the corresponding serial implementation of the same algorithm.
We show that there exists a class of serial algorithms that cannot retain
its structure when partitioned. Parallel programs crafted from a serial
algorithm in this class can produce surprising results. For these cases,
the law is open to abuse. In this paper, we provide a simple rule for identifying
this class of non-structure persistent algorithms.
Finally we conclude that the use of the "serial percentage"
concept in parallel program evaluation is inappropriate for it has
caused much confusion in the parallel processing community for nearly three
decades. This confusion disappears when the processing times are used in
the formulations. Therefore we suggest that processing time based methods
would be the most appropriate for parallel performance evaluation.
2. Equivalence of Gustafson's Law and Amdahl's Law
For clarity, we define the following:
ts : Processing time of the serial part of a program (using 1 processor).
tp(1) : Processing time of the parallel part of the program using 1 processor.
tp(P) : Processing time of the parallel part of the program using P processors.
T(1) : Total processing time of the program including both the serial and the parallel
parts using 1 processor = ![]() .
.
T(P) : Total processing time of the program including both the serial and the parallel
parts using P processors = ![]() .
.
According to the above definitions, we can further define scaled
and non-scaled serial percentages as follows:
a) The scaled percentage of the serial part of the program is
![]() and the scaled parallel part
percentage is then
and the scaled parallel part
percentage is then ![]() .
Note that P occurs in both percentages.
.
Note that P occurs in both percentages.
b) The non-scaled percentage of the serial part program is ![]() and the non-scaled parallel part percentage is
and the non-scaled parallel part percentage is ![]() .
Note that P does not occur in the definitions.
.
Note that P does not occur in the definitions.
It is these two definitions that are the roots of confusion.
For the Amdahl's Law (formulation) we have:
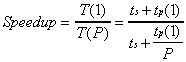 (2.1)
(2.1)
Using the non-scaled percentages, we can reduce (2.1) to the following:
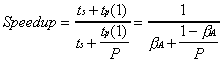 (2.2)
(2.2)
When P approaches infinity, speedup is above bounded by ![]() .
Equation (2.2) projects an unforgiving curve near
.
Equation (2.2) projects an unforgiving curve near ![]() =0
(Figure 1). This was the argument against using MPP systems [1]. However,
few seemed to know how to obtain
=0
(Figure 1). This was the argument against using MPP systems [1]. However,
few seemed to know how to obtain ![]() practically. This is evidenced by a widely cited technical note by Gustafson
[4] that considers
practically. This is evidenced by a widely cited technical note by Gustafson
[4] that considers ![]() to be dependent
of P.
to be dependent
of P.
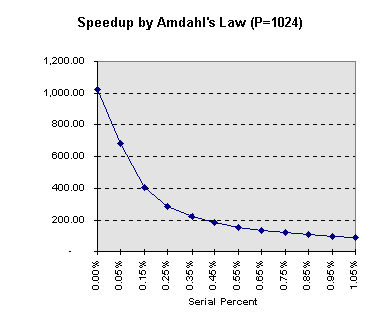
Figure 1. Predicted Speedup Using Amdahl's Law
To justify the almost linear speedup using 1024 processors Gustafson
introduced a new formulation. This is often called the Gustafson's Law
[4]. This new formulation calibrates the serial percentage according to
the total parallel processing time using P processors (![]() ):
):
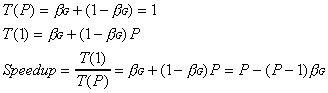 (2.3)
(2.3)
To see the differences, let P=10, a parallel execution
results ![]() =0.6,
namely 40% of the elapsed time is spent on parallel processing (using 10
processors) and 60% is for sequential processing. If we put
=0.6,
namely 40% of the elapsed time is spent on parallel processing (using 10
processors) and 60% is for sequential processing. If we put ![]() in (2.2), then Amdahl's law predicts Speedup = 10/(6.4) =1.6
while Gustafson's law gives Speedup = 10 - 5.4 = 4.6. For
this reason, the speedups computed using Gustafson's formulation have been
called "scaled speedups" in the literature.
in (2.2), then Amdahl's law predicts Speedup = 10/(6.4) =1.6
while Gustafson's law gives Speedup = 10 - 5.4 = 4.6. For
this reason, the speedups computed using Gustafson's formulation have been
called "scaled speedups" in the literature.
This is a mistake. The problem is in the misuse of ![]() in place of
in place of ![]() in Amdahl's formulation.
To calculate
in Amdahl's formulation.
To calculate ![]() we need to derive
we need to derive
![]() . For example, let
. For example, let ![]() seconds be the total elapsed time for the parallel algorithm that gives
the
seconds be the total elapsed time for the parallel algorithm that gives
the ![]() measure. The total sequential
elapsed time
measure. The total sequential
elapsed time ![]() should be 46
= 4 10 + 6 seconds. This yields
should be 46
= 4 10 + 6 seconds. This yields ![]() = 6/46 = 0.13. Then the Amdahl's law gives the identical result:
Speedup = 10/(1.3+0.87) = 4.6.
= 6/46 = 0.13. Then the Amdahl's law gives the identical result:
Speedup = 10/(1.3+0.87) = 4.6.
Mathematically, the two ![]() 's
are related by a simple equation without introducing T(1):
's
are related by a simple equation without introducing T(1):
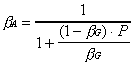 (2.4)
(2.4)
For example, the reported serial percentages (0.4 to 0.8 percent) in
the Gustafson's original paper [4] are really ![]() 's.
In order to use the Amdahl's Law correctly, we must translate
's.
In order to use the Amdahl's Law correctly, we must translate ![]() 's
into
's
into ![]() 's using (2.4). This yields
's using (2.4). This yields
![]() = 0.0004 to 0.0008 percent respectively.
Substituting these to (2.2), Amdahl's formulation predicts Speedup
= 1020 to 1016 using 1024 processors.
= 0.0004 to 0.0008 percent respectively.
Substituting these to (2.2), Amdahl's formulation predicts Speedup
= 1020 to 1016 using 1024 processors.
The above discussion establishes that there is indeed only one Amdahl's
Law but two different formulations. The pessimistic view of Figure 1 is
still valid provided that the actual values of ![]() is not as once thought.
is not as once thought.
3. A Class of Algorithms For Abuse
A prerequisite to applying Amdahl's or Gustafson's formulation is that
the serial and parallel programs take the same number of
total calculation steps for the same input. It can be very tempting
to claim that the Amdahl's Law is "broken" without considering
the prerequisites. In practice, however, breaking the second prerequisite
may be considered "cheating" while breaking the first can be
hard to avoid.
To see this, we define that a serial program is a fixed
implementation of a serial algorithm. Then a parallel
program is a fixed implementation of a parallel algorithm.
An important characteristic of a program is that once compiled, its processing
structure is fixed. Different inputs will travel different paths
in the program resulting in different step counts.
There are three possible relationship between a speedup and the number of processors:
Since every practical parallel program must consolidate the final answer(s)
in one program, the serial percentage in Amdahl's Law is never zero in
practice. Thus, theoretically linear and superlinear speedups are not possible.
In reality, however, there are two factors that can be used to produce linear or superlinear speedups:
Using the above factors, anyone can claim a "break" in Amdahl's
Law by a specially engineered experiment. This was observed in a humorous
note by David Bailey [2].
For example, an O(n2) comparison-based sort algorithm is guaranteed to "break" the law. To see this, we compare the number of worst-case algorithmic steps for sequential and parallel processing:
![]() , if
, if ![]() .
(3.1)
.
(3.1)
The left-hand-side of (3.1) represents the worst-case number of comparisons of the serial sort algorithm, right-hand-side represents the total worst-case parallel computing steps:
In (3.1), the condition is easily satisfied in practical situations.
Since the worst-case communication complexity is O(n), for
any processing environment, (3.1) implies there exists a problem size n
such that a superlinear speedup is guaranteed.
This example illustrates a fact that the O(n2)
sort algorithm cannot retain its structure when crafting a parallel algorithm
from it. In other words, partitioning such a serial algorithm can improved
its efficiency using only one processor.
While it is generally difficult to tell which of the "trick" factors is hidden in a speedup measure, the structure characteristics of the serial algorithm can help us to truly evaluate a parallel performance. Here we develop a simple rule to identify the algorithms that are not structure persistent.
Definition 1. A sequential algorithm is structure persistent
(SP) if all parallel implementations of the same algorithm must
require greater or equal number of calculation steps (including those in
parallel) for all inputs.
Definition 2. A sequential algorithm is non-structure persistent
(NSP) if there exists at least one parallel implementation of the
same algorithm, at least one input, that the parallel implementation requires
less total number of calculation steps (including those in parallel) than
the total pure sequential steps.
Definition 3. A certificate is a verification algorithm
that given a solution to a program it can verify the solution correctness
employing a sub-algorithm of the corresponding solution algorithm.
The certificate concept was inspired by the work by Thomas Cormen, et
al. [3]. For example, the certificate for a sorting algorithm with n
inputs is (n-1) pair-wise comparisons of consecutive elements.
The certificate for a matrix multiplication algorithm is to multiply the
matrices again. And, the certificate for an optimal Traveling Sales Person's
algorithm requires solving the problem again.
Rule 1. Let the complexity of a certificate be f(n)
and solution algorithm g(n), then the solution algorithm
is NSP if ![]() , for some
n>0 and
, for some
n>0 and![]() > 0.
> 0.
A formal proof for this rule is beyond the scope of this paper. We provide
the following examples to show the vast existence of NSP algorithms.
In general, proper partitioning of an NSP algorithm can yield more efficient algorithms. For example, the best partitioning (P value) of the above O(n2) sort algorithm can indeed produce an O(nlgn) algorithm. Re-structuring search paths in a serial program implementing a NP-complete algorithm can often lead to much better performance.
It is important to recognize that the NSP's "instruction
reduction power" really should be eliminated if we want to
apply Amdahl's Law correctly. This can be done by insisting on the best
serial program as the basis for parallel performance evaluation.
For example, for parallel sort, computing speedup using a serial program
with the same partitioning factor as the number of parallel processors
can eliminate superlinear speedup. For NP-complete algorithms, superlinear
speedup can also be eliminated if we can force the sequential program
to follow the best parallel search path. The trouble is, however, there
are too many best serial programs for a given algorithm, since they
are dependent on problem inputs.
It is largely inconvenient to alter a serial program whenever we add
a processor (for the parallel sort) or change an input (for NP-complete
algorithms) for parallel performance evaluation. We may prefer practicality
over precision. Since superlinear speedup is only possible for NSP
algorithms, we can detect the presence of resource factors in a performance
figure if the serial algorithm is SP. This detection can help us
to appreciate the value of a reported parallel performance as how much
less resources are required on parallel processors as compared to a single
processor.
4. Summary
This paper establishes the mathematical equivalence between the Amdahl's
Law and Gustafson's Law. There is indeed only one law but two different
formulations.
Using Amdahl's Law as an argument against massively parallel processing
is not valid. This is because ![]() can be very close to zero for many practical applications. Thus very high
speedups are possible using massively many processors. Gustafson's experiments
are just examples of these applications.
can be very close to zero for many practical applications. Thus very high
speedups are possible using massively many processors. Gustafson's experiments
are just examples of these applications.
Gustafson's formulation gives an illusion that as if P can increase
indefinitely. A closer look finds that the increase in ![]() is affecting speedup negatively. The rate of speedup decrease as P
approaches infinity is exactly the same as depicted by Figure 1,
if we translate the scaled-percentage to a non-scaled percentage. We cannot
observe the speedup impact by P using Gustafson's formulation directly
since it contains a P dependent variable
is affecting speedup negatively. The rate of speedup decrease as P
approaches infinity is exactly the same as depicted by Figure 1,
if we translate the scaled-percentage to a non-scaled percentage. We cannot
observe the speedup impact by P using Gustafson's formulation directly
since it contains a P dependent variable ![]() .
.
Much practical experiences have made many to "feel" the touch
of the unforgiving curve in Figure 1. Perhaps this is the time to end the
debate between "big-cpu" and "many-cpu" in the parallel
processing community. This is because a parallel performance is dependent
on many factors, such as uni-processor power, network speed, I/O
system speed, problem size, problem input and lastly the serial versus
parallel instruction percentages. Therefore there will never be a single
solution for all problems. What we need is a practical engineering tool
that can help us to identify performance critical factors for any algorithm
and processing environment with systematic and practical
steps. This is often called program scalability analysis.
Even though Amdahl's Law is theoretically correct, the serial percentage
is not practically obtainable. For example, if the serial percentage is
to be derived from computational experiments, i.e. recording the total
parallel elapsed time and the parallel-only elapsed time, then it can contain
all overheads, such as communication, synchronization, input/output and
memory access. The law offers no help to separate these factors. On the
other hand, if we obtain the serial percentage by counting the number of
total serial and parallel instructions in a program, then all other overheads
are excluded. However, in this case the predicted speedup may never agree
with the experiments.
Furthermore, the prerequisite of having the same number of total instructions
for both serial and parallel processing adds to the impracticality. This
is because that for NSP algorithms the best serial program
is dependent on the values of the input or the partitioning factor.
Incorrect measure of the serial percentage opens many opportunities for
Amdahl's Law abuse.
In the last three decades, as we have witnessed, the use of the "serial percentage" concept has caused much confusion in the parallel processing community. The confusion disappears when we start using sequential and parallel times as the basis for parallel performance evaluation. A significant additional benefit using time for parallel algorithm evaluation is that all performance critical factors can be evaluated in the same domain. Therefore program scalability analysis can be conducted for sequential and parallel programs. In comparison, it is impossible to use Amdahl's Law to conduct program scalability analysis.
Author's Biography:
Dr. Yuan Shi earned his Master and Ph.D Degrees from University of Pennsylvania, Philadelphia, in 1983 and 1984 respectively. He is currently an Associate Professor in the CIS Department of Temple University. He is also the Interim Director for Center for Advanced Computing and Communications at Temple University since 1993, and serves as a Technical Advisory Committee member for Ben Franklin Technology Center in Philadelphia since 1993. He is the inventor of two patents in areas of heterogeneous parallel programming system and parallel computer architecture.