CIS 9615. Analysis of Algorithms

Dynamic Programming and Memoization

 

1. The idea

Issue: overlapping subproblems in divide-and-conquer.

Example: Fibonacci numbers

Direct recursive algorithm: 

    Fibonacci-R(n)
    1  if n < 2
    2      then return n
    3  return Fibonacci-R(n-1) + Fibonacci-R(n-2)
Complexity: Θ(φn), φ ∼ 1.618 ("golden ratio").

Repeated work: to calculate F(4), the algorithm calculates F(3) and F(2) separately though in calculating F(3), F(2) is already calculated.

Dynamic programming: to turn a "top-down" recursion into a "bottom-up" construction. 

    Fibonacci-DP(n)
    1  A[0] <- 0        // assume 0 is a valid index
    2  A[1] <- 1
    3  for j <- 2 to n
    4      A[j] <- A[j-1] + A[j-2]
    5  return A[n]
Complexity: Θ(n).

Memoization: a variation of dynamic programming that keeps the efficiency, while maintaining a top-down strategy. 

    Fibonacci-M(n)
    1  A[0] <- 0        // assume 0 is a valid index
    2  A[1] <- 1
    3  for j <- 2 to n
    4      A[j] <- -1
    5  Fibonacci-M2(A, n)

    Fibonacci-M2(A, n)
    1  if A[n] < 0
    2      then A[n] <- Fibonacci-M2(A, n-1) + Fibonacci-M2(A, n-2)
    3  return A[n]
Complexity: also Θ(n).

Dynamic programming used in optimization: the optimal solution corresponds to a special way to divide the problem into sub-problems. When different ways of division are compared, it is quite common that some sub-problems are involved in multiple times. The complexity of such a solution comes from the need of keeping intermediate results, as well as remembering the structure of the optimal solution, i.e., how the problem is divided into sub-problems, step by step.

 

2. Example: matrix-chain multiplication

Matrix multiplication: The product of a p-by-q matrix and a q-by-r matrix is a p-by-r matrix, which contains p*r elements, each calculated from q scalar multiplications, so the overall cost is proportional to p*q*r.

To calculate the product of a matrix-chain A1A2...An, n-1 matrix multiplications are needed, though different orders have different costs.

For matrix-chain A1A2A3, if the three have sizes 10-by-2, 2-by-20, and 20-by-5, respectively, then the cost of (A1A2)A3 is 10*2*20 + 10*20*5 = 1400, while the cost of A1(A2A3) is 2*20*5 + 10*2*5 = 300.

For matrix-chain Ai...Aj where each Ak has dimensions Pk-1-by-Pk, the minimum cost of the product m[i,j] corresponds to the best way to cut it into Ai...Ak and Ak+1...Aj: 

    m[i, j] = 0                                         if i = j
              min{ m[i,k] + m[k+1,j] + Pi-1PkPj }        if i < j
Use dynamic programming to solve this problem: calculating m for sub-chains with increasing length, and using another matrix s to keep the cutting point k for each m[i,j].


Example: Given the following matrix dimensions:
A1 is 30-by-35
A2 is 35-by-15
A3 is 15-by-5
A4 is 5-by-10
A5 is 10-by-20
A6 is 20-by-25

then the output of the program is

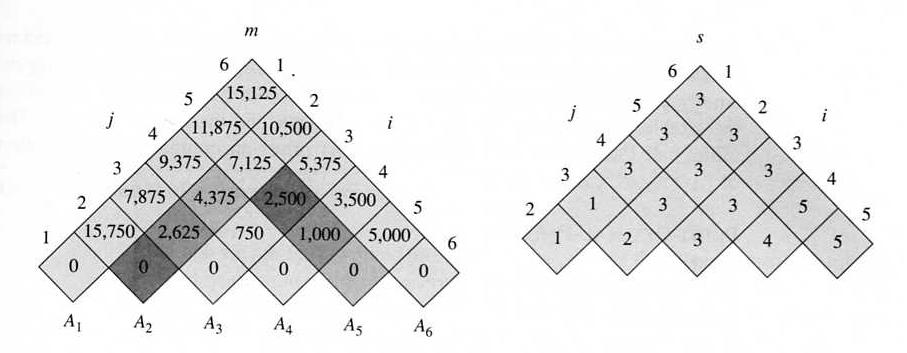
which means that A1A2A3A4A5A6 should be calculated as (A1(A2A3))((A4A5)A6), and the number of scalar multiplication is 15,125.

Time cost: Θ(n3), space cost: Θ(n2).

Please note that this algorithm determines the best order to carry out the matrix multiplications, without doing the multiplications themselves.

 

3. More examples

(1) Longest Common Subsequence (LCS)

For sequence X and Y, their LCS can be recursively constructed: 

c[i,j] = 0                         if i == 0 or j == 0
         c[i-1,j-1]+1              if i,j>0 and Xi == Yj
         max(c[i,j-1],c[i-1,j])    if i,j>0 and Xi != Yj
Time cost: Θ(mn). Space cost: Θ(mn). Demo applet.

(2) Optimal Binary Search Tree

If the keys in a BST have different probabilities to be searched, then a balanced tree may not give the lowest average cost (though it gives the lowest worst cost). Using dynamic programming, BST with optimal average search time can be built, in a way similar to matrix-chain multiplication.

Time cost: Θ(n3). Space cost: Θ(n2). Demo applet.