B-trees and Amortized Analysis
Various types of binary tree, including BST and heap, can be extended into trees where a node can have more than two successors. These data structures are similar to binary trees in certain aspects, but also have different properties. For example, Prefix tree (or trie) is an n-ary search tree where the key value is used one character (or digit) per level in the search process.
A 2-3 tree is such a tree where each node has 2 or 3 children (subtrees), and they are separated by 1 or 2 key values. Within the tree, a 2-node has 2 children and 1 key, while a 3-node has 3 children and 2 keys. All leaves are at the same level, and all keys are "sorted horizontally" as in a BST.
[|7|]
/ \
[|3|] [|11|15|]
/ \ / | \
[1] [5] [9] [13] [17 19]
Searching a 2-3 tree is similar to searching a BST, except that within each 3-node, in the worst case two comparisons are needed.
Insertion: In a 2-3 tree, a new key value is initially inserted into a leaf where the search stops, according to the order of a search tree. After that, there are the following possibilities:
Deletion: To remove a key value from a 2-3 tree, the first step is to search for it. If it is in a leaf, simply remove it. If it is in an internal node, replace the deleted key by its successor (or predecessor), which must be in a leaf. After that, there are the following possibilities:
2-3-4 trees extend 2-3 trees by allowing 4-nodes, so each non-leaf node can have 2, 3, or 4 children.
The operations of 2-3-4 trees are similar to those of 2-3 trees.
There is a mapping between a 2-3-4 tree and a Red-Black tree. In the following, a lower case letter represents a key, and an upper case letter represents a subtree.
[|b|] b
/ \ / \
A C A C
[|b|d|] b d
/ | \ / \ / \
A C E A d or b E
/ \ / \
C E A C
[|b|d|f|] d
/ | | \ / \
A C E G b f
/ \ / \
A C E G
Since each node in a 2-3-4 tree corresponds to one black node (plus at most two red nodes) in a Red-Black tree, the height of a 2-3-4 tree corresponds to the number of black nodes in the path from the root to a leaf in a Red-Black tree, which is half of the number of comparisons in the worst case.
A B-tree with a minimum degree t (t is 2 or more) has the following properties:
An alternative approach defines an order-m B-tree, where m is the maximum number of children of a node, and the minimum number cannot be less than half of m (i.e., is ceiling(m/2)) except the root can have as few as 2 children. Therefore 2-3 tree and 2-3-4 tree are B-tree of order 3 and 4, respectively. This definition is more general than the previous one using "degree", as the maximum number of children can be odd or even.
Example: an order-5 B-tree (where each node contains 2-4 keys and 3-5 children)
[|20|30|42|]
/ | | \
/--------/ / \ \--------\
/ / \ \
[ 10 15 ] [ 25 28 ] [ 32 34 ] [ 44 55 ]
A search algorithm starts at node x and look for key k:

Insertion: Insert can be seen as a search (for the inserting position) followed by the actual insert of the key. As in 2-3 and 2-3-4 trees, insertion happens in a leaf node until the leaf node has m keys. Then it is split into two nodes and the middle key is sent up to the parent node.
Starting from the above B-tree, after adding 8, 18, 26, 36, 39, 43 we have
[|20|30|42|]
/ | | \
/-------------/ / \ \---------------\
/ / \ \
[ 8 10 15 18 ] [ 25 26 28 ] [ 32 34 36 39 ] [ 43 44 55 ]
At this point two of the leaf nodes are full and two are not. Let's insert in one of the full leaf nodes and see what happens.
Insert 37: 37 is not in the tree, so it is inserted in the child node between 30 and 42. That node would contain 32 34 36 37 39, which is too big, so it splits into two nodes and pass the middle value (36) up.
[|20|30|36|42|]
/ | | | \
/-----------------/ /-/ | \-\ \------------\
/ / | \ \
[ 8 10 15 18 ] [ 25 26 28 ] [ 32 34 ] [ 37 39 ] [ 43 44 55 ]
Now let's insert in the other node which is full. Remember that all insertions begin at a leaf node. Insert 12 in leftmost leaf: 8 10 12 15 18 -- too big, split and pass 12 up.
Parent node becomes 12 20 30 36 42 -- too big, split and pass 30 up to become the new root (it is fine if the root has less than m/2 entries). From this example, we see that B-Trees actually grow in a bottom-up manner (at root), rather than top-down (at leaf).
[|30|]
/ \
/ \
[|12|20|] [|36|42|]
/---------------/ / | | \ \--------------\
/ /-------/ | | \------\ \
/ / / \ \ \
[ 8 10 ] [ 15 18 ] [ 25 26 28 ] [ 32 34 ] [ 37 39 ] [ 43 44 55 ]
A textbook example (t = 3):
 For deletion, the algorithm can delete a key that is either in a leaf or a non-leaf node. Again, deletion consists of a search, and, if the key is found in the tree, an actual deletion of it.
For deletion, the algorithm can delete a key that is either in a leaf or a non-leaf node. Again, deletion consists of a search, and, if the key is found in the tree, an actual deletion of it.
If we delete a key in a leaf node, there is no problem unless the leaf node becomes too small. Then we have to merge it with a sibling leaf (plus the key in the parent separating them). If the resulting node has too many keys we have to split it in two and send the middle key up as in insertion.
If the key to be deleted is not in a leaf node, then it is replaced by the next larger key in the B-tree. Similar to finding the successor in a BST. Follow pointer to next child node and then follow all leftmost pointers until a leaf is reached. Replace key to be deleted with smallest key in the leaf node and then delete that key from the leaf. Merge with an adjacent leaf if necessary (see process for deleting from a leaf node).
Let us delete 44 (in a leaf) from the above tree:
[|30|]
/ \
/ \
[|12|20|] [|36|42|]
/---------------/ / | | \ \--------------\
/ /-------/ | | \------\ \
/ / / \ \ \
[ 8 10 ] [ 15 18 ] [ 25 26 28 ] [ 32 34 ] [ 37 39 ] [ 43 55 ]
Now delete 18, in a leaf. Since the new leaf is too small, merge with the leaf to its right to become [15 20 25 26 28], then split and move 25 up. The total effect is like a rotation in an AVL Tree. It can be seen as getting a key from a sibling via the parent.
[|30|]
/ \
/ \
[|12|25|] [|36|42|]
/---------------/ / | | \ \--------------\
/ /-------/ | | \------\ \
/ / / \ \ \
[ 8 10 ] [ 15 20 ] [ 26 28 ] [ 32 34 ] [ 37 39 ] [ 43 55 ]
Delete 36, replace with 37, delete old 37, merge [39] with [32, 34], plus 37 -- finally get one full node.
[|30|]
/ \
/ \
[|12|25|] [|42|]
/---------------/ / | | \
/ /-------/ | | \----------\
/ / / \ \
[ 8 10 ] [ 15 20 ] [ 26 28 ] [ 32 34 37 39 ] [ 43 55 ]
Now node with 42 has only one key, so it must be merged to become [12 25 30 42] which serves as the new root. Tree height is reduced by 1.
[|12|25|30|42|]
/---------------/ / | | \
/ /-------/ | | \----------\
/ / / \ \
[ 8 10 ] [ 15 20 ] [ 26 28 ] [ 32 34 37 39 ] [ 43 55 ]
Every n-node B-tree has height O(lg n), and every major operation works on a path from the root to a leaf.
The delete algorithm in the textbook is slightly different, though with similar results. Example (t = 3):
 B+ tree is a variation of B-tree that is optimized primarily for database indexing and file systems. In a B+ tree, data is stored only in the leaf nodes. The internal nodes store keys only, which are duplicated from leaf nodes. Leaf nodes are linked sequentially.
B+ tree is a variation of B-tree that is optimized primarily for database indexing and file systems. In a B+ tree, data is stored only in the leaf nodes. The internal nodes store keys only, which are duplicated from leaf nodes. Leaf nodes are linked sequentially.
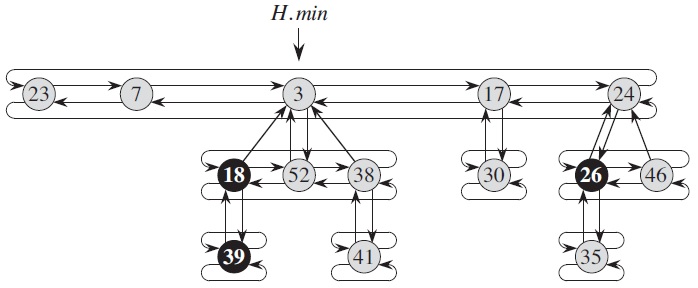
In a Fibonacci heap, each node contains a pointer to its parent, a pointer to an arbitrary child, and two pointers to its siblings. The children of a node are linked together in a circular, doubly linked "child list" in an arbitrary order. The "degree" of a root indicates its number of children.
Defined in this way, certain operations can be carried out in O(1) time. INSERT simply adds the new node as the root of a new tree and update the heap root when the new key is smaller than the previous root; UNION combines two trees by let the larger root become a child of the smaller root. Complicated structure maintenance only happens after the minimum value (heap root) is removed. After that the children of the removed node are treated as roots of separate trees, then the trees of the same degree are union-ed repeatedly, as in the following example, where an array A is used to remember trees of each degree.
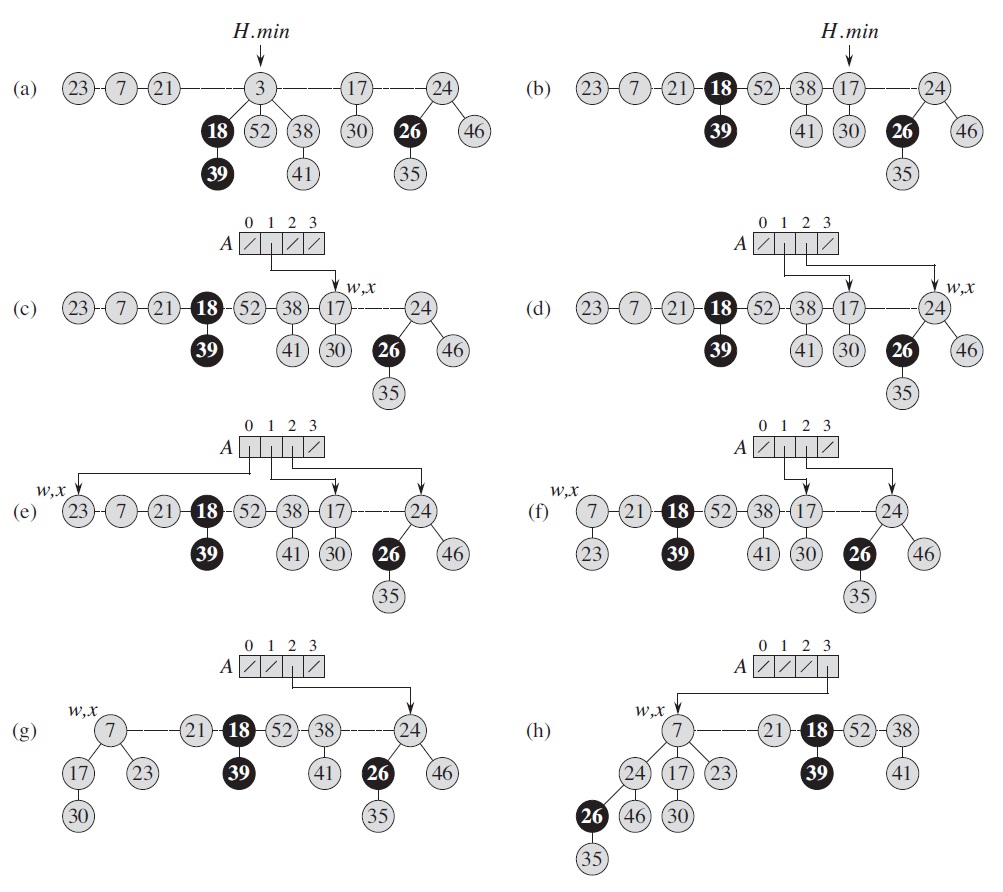
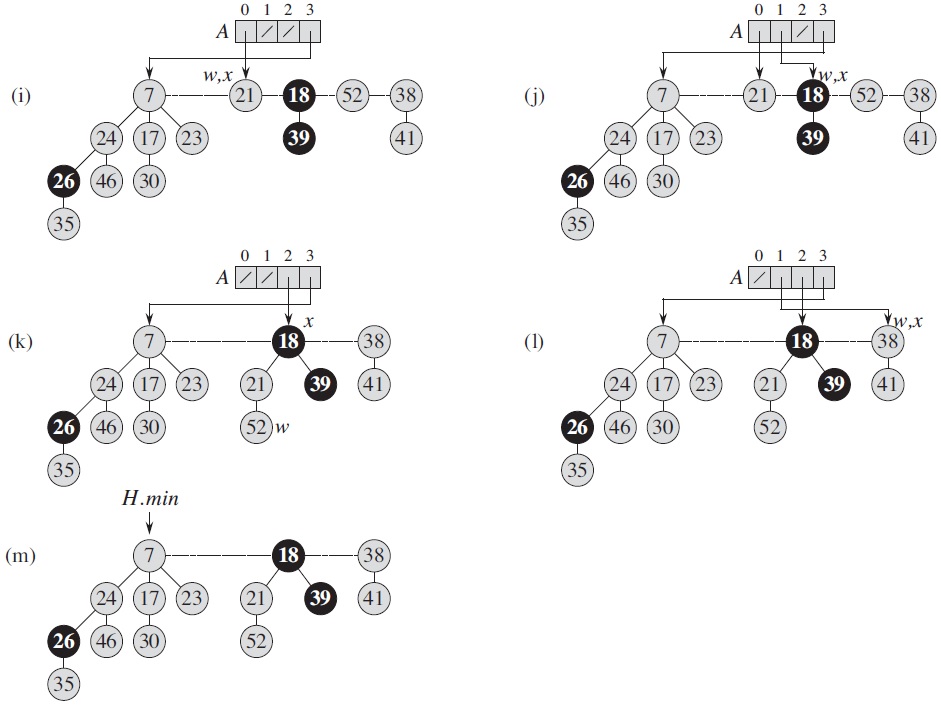
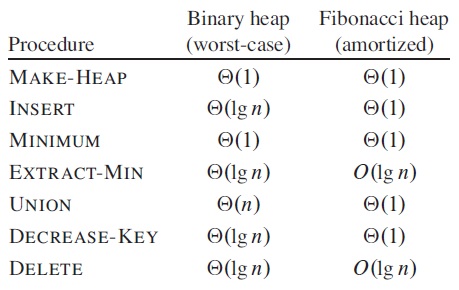
For this type of structures, for each operation it usually makes more sense to analyze its average cost when repeated in the worst case, which is called the "amortized cost" operation. For example, if a stack is implemented as an array with fixed length n, operation push usually takes O(1) time, but the worst case is O(n) when it is full and space reallocation happens. Since the latter happens once after the former happens n times, the amortized cost of the operation is still O(1).
Here is a comparison between binary heap and Fibonacci heap: