Binary Search Trees
A binary tree is a tree where each node can only have a left successor and a right successor, or, recursively, as either empty or a root node with a left subtree and a right subtree (both are binary trees).
To implement a binary tree, usually each node has two pointers to its successors, though it may also contains a pointer to its predecessor.

To implement a (general) tree, it is possible to use an array or linked list to point to its successors, or convert the tree into a corresponding binary tree, following the "first child : left child, next sibling : right child" mapping.
A complete binary tree can be efficiently stored in an array (as in heaps), though for binary trees in general, too much memory will be wasted using that approach.
A systematic visit of the nodes of a tree is called "walk" or "traversal". For a binary tree, there are three common walk orders, all defined recursively:

These orders can be followed manually by tracing the outline drawn around the tree:
For such a binary tree, search is similar to binary search in a sorted array. The algorithm can be either recursive or iterative.

The path the algorithm following is from the root to a node where the key to be searched is or should be in the tree, therefore the running time is proportional to the length of the path, and the worst case running time is proportional to the height of the tree.
We can take the search for the minimum and maximum keys as special cases of the search operation. In these cases, the comparisons in the path become unnecessary, and the algorithm simply goes to the end of one direction: left for the minimum and right for the maximum.
Given a node x in a binary search tree, its (inorder) successor is the node with the smallest key greater than x.key, so in an inorder tree walk this node will immediately follow x. The following algorithm requires the pointer to parent in each node. If x has a right subtree, then its successor is the minimum node in it, otherwise its successor is its closest ancestor that x is in its left subtree.

Repeatedly calling Tree-Successor will give us a non-recursive inorder tree walk algorithm.
All the search algorithms on BST run in O(h) time, where h is the height of the tree.
The following algorithm inserts node z into BST T (assume z is not already in T):

The deletion algorithm is more complicated, because after a non-leaf node is deleted, the "hole" in the structure needs to be filled by another node. There are three possibilities:
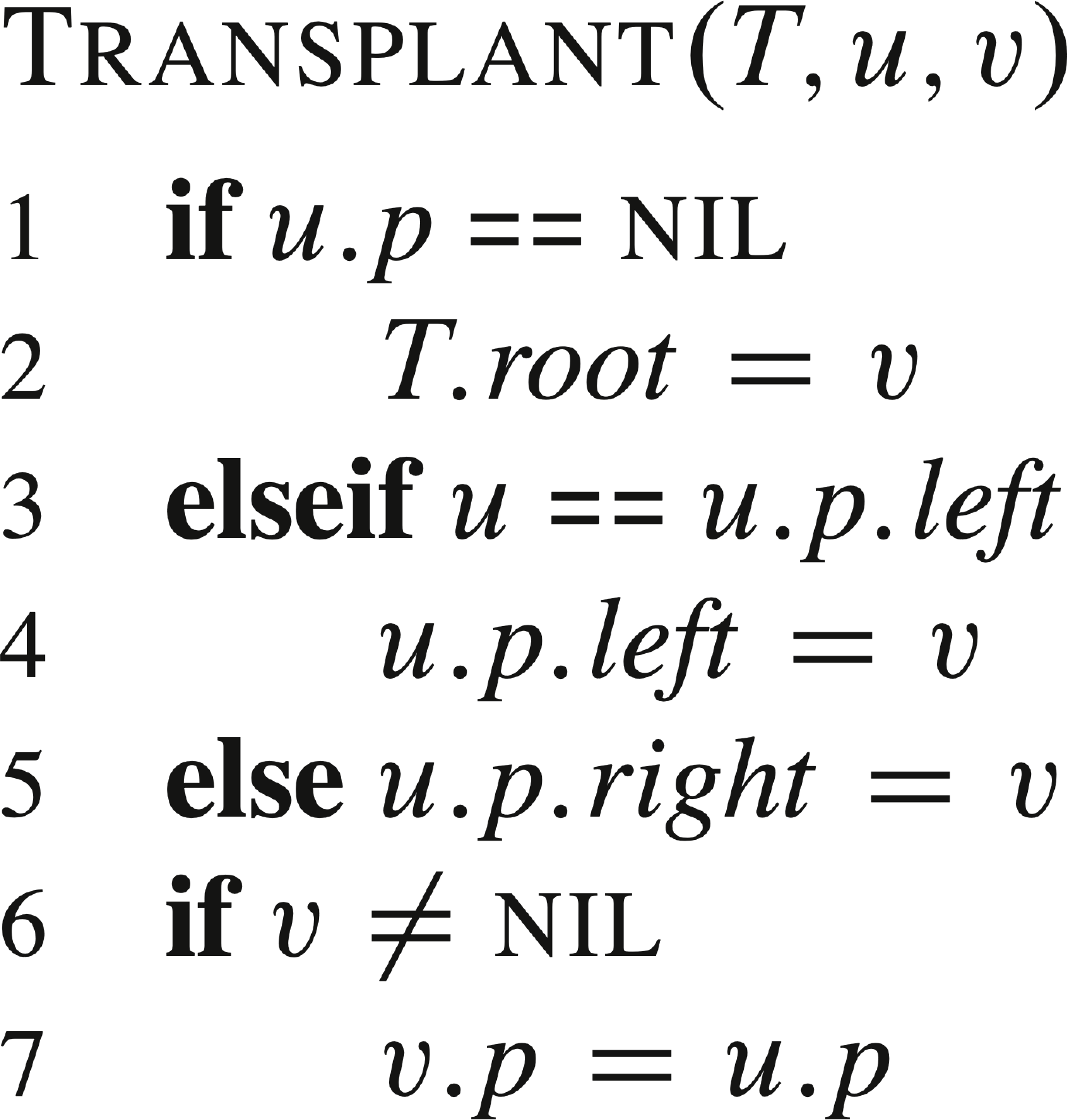
In the following algorithm, z is an input argument referring to the node to be deleted from the BST T, and the local variable y refers to its successor.

Both above algorithms have run time O(h).
Since in BST all major operations have run time O(h), the height of a binary search tree determines the worst-case run time. For a binary tree with n nodes, the shortest tree (complete binary tree) has a height h = Θ(lg(n)), and the highest tree (linear list) has a height h = Θ(n). A randomly formed BST has an expected height h = Θ(lg(n)).