Learning: Symbolic Approaches
Roughly speaking, learning is the ability of an agent to improve its behavior based on experience. There are two critical aspects in such a definition:
One approach is to gradually refining the hypothesis space. If all hypothesis are Boolean expressions, then the version space contains the hypothesis that are consistent with the examples. The learning is carried out by a candidate-elimination algorithm. In this process, a positive example specifies what a concept should include, and a negative example specifies what it should not include. They can be used to eliminate candidates that are either too general or too specific, so as to reduce the version space.
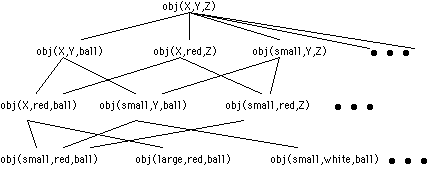
A Prolog implementation of this algorithm is here that works on the following hypothesis space, where each object is specified by size, color, and shape.

If the examples are described by their attribute values, but not classified, concepts can be learned via unsupervised learning or clustering by recursively merge or split the current class(es), with the hope to achieve the minimum intra-class distances and the maximum inter-class distances.
When the system needs to distinguish the instances of multiple given concepts, the procedure is sometimes represented as a "decision tree": given an object or a situation specified by a set of attributes, the tree decides which concept it belongs to. Each internal node in the tree represents a test on one of those attributes, and the branches from the node are labeled with the possible outcomes of the test. Each leaf node is a Boolean classifier for the input instance. It is similar to the "20 Questions" game.
To learn an efficient decision tree: to recursively split the class into subclasses using a property, until all subclasses contains examples of the same categorization. When there are multiple ways to split a class, try to do so as evenly as possible.
Ryszard S. Michalski proposed an inferential theory of learning, in which various types non-deductive inference, like induction and analogy, are formalized in the framework of predicate logic, as ways to generate useful hypotheses.
Using inductive logic programming, general relationships (like the "rules" in Prolog) can be derived from concrete examples (like the "facts" in Prolog). The approach is similar to that of supervised concept learning (a tutorial). At the current time, this technique only produces relatively simple programs.
The approach taken in NARS is based on the assumption that quantitative measurement of evidential support is necessary in inferential learning. The working examples can help to explain how the system works.
Closely related to genetic algorithm, in genetic programming a program (typically in a functional programming language, such as Lisp) is represented as a binary tree.
Genetic programming takes four steps to solve problems: