Packets: For a variety of reasons data in
networks is transmitted in packets, which are sequences of octets (i.e.
bytes). [Some reasons: cheaper to deal with loss or corruption of small
packets than with long full messages; easier to share communication channels
between concurrent communicating entities since there are no long messages
for whose transmission all have to wait; usually less total transfer time
in a store-and-forward multi-hop network.]
Usually packets are transmitted asynchronously, so we need to know
when the packet starts and when it ends [in the case of RS232 characters
we had a start and an end bit]. In general the problem of recognizing start
and end of a packet is called the framing problem.
One possible way to represent a packet is by starting it with a special
character, say SOH = 0x01, and ending it with a special character, say
EOT=0x04. Then one can recognize a packet by looking for these characters.
Of course, we need to make sure that SOH and EOT appear only at the
beginning and end of packets. This is done with byte stuffing: that
is replacing in the data each occurrence of SOH, EOT, and ESC=0x1B, with
ESC SOH, ESC EOT, and ESC ESC respectively (in bit oriented transmission
like in HDLC one encounters bit stuffing, where one uses the pattern
01111110 to start and end a packet. Of course then in the data one has to
prevent the occurrence of 6 consecutive 1s. This is done always
inserting a 0 after five data 1s.).
Error Detection:
Error detection
is a form of error control [other forms of error control, for error
recovery, are Forward Error Recovery and Automatic Repeat Request [ARQ]. ARQ involves
Positive Acknowledgement,
Retransmission after Timeout, Negative Acknowledgement and Retransmission.
We will talk more about ARQ when we discuss data link level protocols.].
In general when a frame is sent, it may be lost in transit or it may be
delivered corrupted (one hopes it gets there unchanged).
The loss-in-transit of a frame is recognised by the sender by setting a
time-out on the expected reception of an acknowledgement from
the receiver.
Here we describe
three methods that allow the receiver to detect errors, that is, to know
with some probability that it has received what the sender sent.
00011100 11011110 11100110 10101001 ======= 10001101 Even parity octetWe will be able to detect any single bit error in this block [because one of the parity bits will be inconsistent with the corresponding column].
000111001 110111100 111001101 101010010 ========= 100011010will be able to detect and correct a single bit error [if you change any single bit both the horizontal and vertical parity bits become inconsistent, thus identifying both the row and the column of the error bit].
|6C|6C| "ll"
|6F|20| "o "
|77|6F| "wo"
|72|6C| "rl"
|64|2E| "d."
======
|71|FC| Checksum
Alternatively the checksum can be computed by adding each individual byte and using the carry as an additional addend. Checksums are easy to compute and have a fairly good capacity to detect errors. Unfortunately they do not detect simple forms of errors. For example, suppose that errors reverse the value of the second bit of each word being transmitted. If these words had the same number of 1s and 0s as second bits then the error will not be detected. Experimental studies indicate that about 1/5000 packets are with errors (the majority of errors are introduced at the routers). Consequently since the checksum can fail to detect an error at best in 1/64k cases, we have that one packet in (5000*64k) =~330M packets will be with an error and its checksum will say that there is no error! So something else must be done to detect such errors (for example as we will see in security we can use digests).
Here is a routine to compute the checksum of an array of short unsigned integers:
unsigned short checksum(unsigned short *buffer, int count)
{
unsigned long int csum = 0;
while (count--) {
csum += *buffer++;
if (csum & 0xFFFF0000){ /* There is a carry bit */
csum &= 0x0000FFFF; /* Remove the carry bit */
csum++; /* and add it to csum */
}
}
return (csum & 0xFFFF); /* The checksum computed in the
internet is really ~(csum & 0xFFFF)
that is the 1-complement, so that at
receiving end the total sum, including
received checksum, is zero. Also, since
1-complement has two representations for 0,
0000...00 and 1111...11, this can give a bit
of information, a flag that can be used
by the network protocols.
*/
}
Then an irreducible polynomial P (it is for polynomials the same as a prime for numbers) is used to compute the modulo of the data polynomial. This modulo is taken as the CRC and appended to the data. The nice thing is that the modulo can be computed using simple circuits: XOR gates and shift registers initially containing 0. Here is an example of circuit for computing the CRC using as P the polynomial
|In
v X**16 X**12 X**5 1
X------------------>+--------------------------->+----------------------+
^ | | |
| +--+--+--+--+ v +--+--+--+--+--+--+--+ v +--+--+--+--+--+ v
+<--| | | | |<--X<--| | | | | | | |<--X<--| | | | | |<--+
| +--+--+--+--+ +--+--+--+--+--+--+--+ +--+--+--+--+--+
vout
To understand this structure, imagine that we are transmitting a single 1.
Then, since it will be appended to the remainder, it is as if the 1 was
multiplied by X**16, the degree of P. That is we obtain
X**16 1
| |
v v
10000000000000000
the remainder of this when dividing by P is
X**12 X**5 1
| | |
v v v
0001000000100001
which is just P eliminating its leading term. The Xor gates are positioned in the places
where we have the 1s.
When the message (data plus remainder) is received, the data
will cause that same remainder to be computed in the receiver's register. When the
original remainder is received, the two remainders will cancel each other
leaving 0s in the registers.
Here is how things work out for our original data 100100001100101
Arriving |
Bits | Content of registers
=================================
1 0000 0000000 00000
0 0001 0000001 00001
0 0010 0000010 00010
1 0100 0000100 00100
0 1001 0001001 01001
---------------------------------
0 0011 0010011 10011
0 0110 0100111 00110
0 1100 1001110 01100
1 1000 0011101 11001
1 0000 0111011 10010
---------------------------------
0 0001 1110110 00101
0 0011 1101100 01010
1 0111 1011000 10100
0 1110 0110000 01001
1 1101 1100001 10011
---------------------------------
1011 1000011 00110
Thus the message (data plus remainder) is 100100001100101 1011100001100110
More formally, if P(x) is the irreducible polynomial and M(x) is the message we are sending, the circuit operates as if we were sending the code C(x) = (x**r)*M(x) + R(x), where r is the degree of P(x) and R(x) is the remainder of the divisions of (x**r)*M(x) by P(x). Since the dividend is equal to the divisor*quotient + remainder, C(x) is just P(x)*quotient [since R(x) + R(x) is just 0 in binary arithmetic, and P(x) is the divisor). Thus the receiver will receive just P(x)*quotient and dividing it by P(x) will have a zero remainder. Of course if the code is corrupted during transmission the remainder at the receiver will not be 0. In fact, if the error is E(x), the remainder will be E(x)/P(x).
If you use a CRC polynomial of degree r, then that use will allow us to detect errors in the message of up to r bits. If there are more than r bit errors, then there is no guaranty that we will detect the error, but it is likely that we do so (the probability of undeteced error is 1/2^r).
Though Cyclic Redundancy Checks may be greatly superior to checksums, checksums may be preferred when computation speed is of the essence. For example in the IP protocol (that we study later) they use checksums [and to do them faster the sender computes the 1-complement checksum, the receiver computes the checksum and then adds it to the sender's checksum to obtain 0 - thus saving on the time it would take if we did checksums at both sender and receiver and then compared]. Ethernet uses 32-bit CRC.
Suppose I have two bit vectors, for instance 0110101 and 0100111, their Hamming Distance is the number of bit where they differ (in our case the Hamming distance is 2). Then, if we use a set S of bit vectors such that the minimal Hamming distance between two elements of S is d, then
Here is an example of 1 bit error correcting code (minimum distance = 3): We are given the following 4-bit vectors.
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111We represent them with the 7-bit vectors (the original 4 plus 3)
0000 000 0001 101 0010 111 0011 010 0100 011 0101 110 0110 100 0111 001 1000 110 1001 011 1010 001 1011 100 1100 101 1101 000 1110 010 1111 111where the three additional bits are parity bits obtained considering, in order,
bits 1 3 4 to compute the 5thbit bits 1 2 3 to compute the 6thbit bits 2 3 4 to compute the 7thbitthat is
(bit1 + bit3 + bit4 + bit5 = 0 modulo 2) (bit1 + bit2 + bit3 + bit6 = 0 modulo 2) ( bit2 + bit3 + bit4 + bit7 = 0 modulo 2)You can check by looking at each pair of 7-bit vector that the Hamming Distance now is 3. Thus we can correct a one bit error. You might, in a night when sleep is late in coming, think why parity bits computed this way worked!
Automatic Repeat Request (ARQ):
A basic way of dealing with transmission errors, detected either by the receiver (error detection as described earlier), or at the transmitter (no acknowledgement within timeout) is to retransmit data. Methods based on this idea are called ARQ (Automatic Repeat Request) methods. Three such methods are in common use:
Tt 1 Tp propagationTime
--------- = -------- where a = --- = ----------------- =
Tt + 2*Tp 1 + 2*a Tt transmissionTime
propagationTime * dataRate
= -------------------------- =
frameSize
sizeofDataInTransit
= -------------------
frameSize
So the utilization in our example in Ethernet is almost 100%.
Note the delay-throughput-product = sizeofDataInTransit in "a".
As the ratio of this product to the size of the frame grows, so does
the efficiency of the transmission diminish.
(1 - P)
---------
1 + 2*a
[this result is obtained reasoning as when we computed the round robin time
in the notes on performance evaluation.]
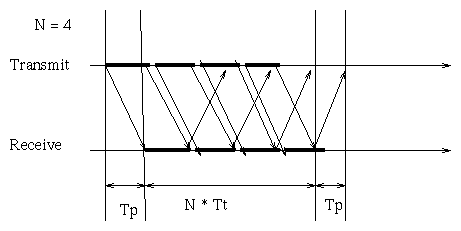
If we consider instead the Go-Back-N ARQ or the Selective-Repeat ARQ the transmission of ACKs is overlapped with the transmission of the frames. Thus the utilization, without worrying about errors, becomes
N
/ ------- if N < 1 + 2*a
| 1 + 2*a
utilization = |
|
\ 1 otherwise
This can be understood with the following observations: