CIS 307: Logical Clocks
Read Tanenbaum, Distributed Operating Systems, Chapter 3, pages 118 - 133
and Chapter 10, pages 540 - 544.
We would like to order the events occurring in a distributed system in such
a way as to reflect their possible causal connections. Certainly if an event
A happens before an even B, then A cannot have been caused by B. In this
situation we cannot say that A is the directed cause of B,
but we cannot exclude that A might have influenced B.
We want to characterize this "happened-before" relation on
events. We will consider only two kinds of events, the sending of a message
and the receiving of a message.
- If events e1 and e2 occur in the same system and e1 occurs before e2 (there
is no problem to determine this in a single system) then
e1 happened-before e2, written e1 -> e2
- If event e1 is the sending of a message and e2 is the receiving of that
message, then e1 happened-before e2
- If e1 -> e2 and e2 -> e3 then e1 -> e3
The -> relation is a partial order. Given events e1 and e2
it is not true that either they are the same event or one happened-before the other.
These events may be unrelated.
Events that are not ordered by happened-before are said to be
concurrent.
This characterization of happened-before is unsatisfactory since, given two
events, it is not immediate (think of the time it takes to evaluate a
transitive relation) to determine if one event happened before the other
or if they are concurrent. We would like a clock C that applied to an
event returns a number so that the following holds:
(1) If e1 -> e2 then C(e1) < C(e2)
We can define one such C, a logical clock, as follows:
- On each computer i we start with a clock Li set at 0
- If e is the sending of a message, then increment the local clock Li,
set C(e) to Li and timestamp the message with Li
- If e is the receiving at node i of a message with timestamp t, then set
the local clock and C(e) to max{t, Li}+1
[We could have started the local clocks with their values set
to the same value greater or equal to 0
and using as increments, instead of 1, any value greater than 0. The
resulting time still would satisfy (1)]
Here is an example showing events a,b,c,d,e,f,g,h,i,j and the corresponding
local clocks:
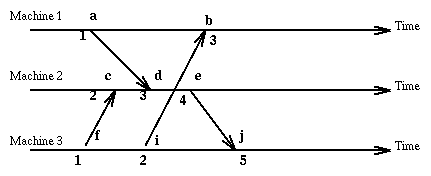
Since the method we have chosen allows different events (on different machines)
to have the same logical clock value, we extent the clock value with a number
representing the machine where the event occurred [i, C(e)] and order these
pairs according to the rule:
[i,C(e1)] < [j,C(e2)] iff C(e1) < C(e2) or [C(e1)=C(e2) and i<j]
Here is an example showing the same events but now tagged with numbers that
totally order them:
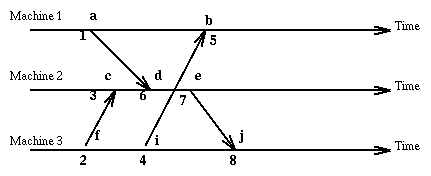
A problem of the logical clocks considered above is that they do not represent
faithfully the happened-before relation. Namely, it is not true that
(2) If C(e1) < C(e2) then e1 -> e2
It would be nice to have logical clocks that would allow us to answer
precisely questions of concurrency and dependency. We can do it by using
clock values that are vectors of numbers, one for each computer system
and then comparing vector values v and u with the rule
u < v iff ((for all components i, u[i]is less or equal to v[i]) and
(there is a j such u[j]<v[j]))
Here are the rules on vector clocks in a system with n computers:
- Each computer starts with a local clock set at [0,0,..,0]
- When on computer i there is a sending event, increment the ith component
of the clock by 1 leaving other components unchanged, then tag both the event
and the message with this value
- When on computer i there is a receiving event,
form a new local clock value taking the componentwise maximum of the local
clock and the time stamp on the arriving message.
Then increment by 1 the ith component.
Finally tag the event with this value.
Here is our old example using vector clock values.
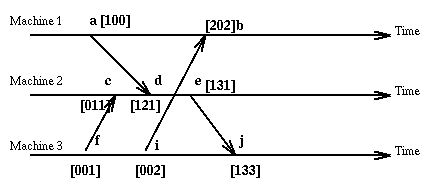
Of course nothing is perfect. Though vector clocks allow to represent faithfully the
happened before relation between events, they result in
big time stamps and requires that we know in advance the number and identities of the sites involved.
All logical clocks, whether scalar or vector, suffer of a basic problem:
though they represent that an even occurred (or not) before another, they do not
represent before by how much, that is, there is no measure of elapsed
time. In particular we cannot use logical clocks for timeouts, we need instead
a wallclock (i.e. an old fashioned clock, possibly synchronized).
Messages with FIFO Property and the Causal Ordering of messages
If we send two datagrams from host n1 to host n2 using the IP or UDP protocol
we are not guaranteed that they will be received in the
order they were sent. If instead we send data using the TCP protocol we
are guaranteed that it will be received in the order it was sent.
Let's use the following notation,
given a message m, SEND(m) is the event of sending the
message m, and RECEIVE(m) is the event of receiving the message m.
We say that a messaging system satisfies the
FIFO propertyif: when m1 and m2 are messages and we
have SEND(m1) -> SEND(m2) then RECEIVE(m1) -> RECEIVE(m2). When this
property is satisfied we have a natural ordering (partial) for messages,
called causal ordering of messages:
m1 -> m2 if SEND(m1) -> SEND(m2). Note that the following situations
are forbidden in a messaging system with the FIFO property:
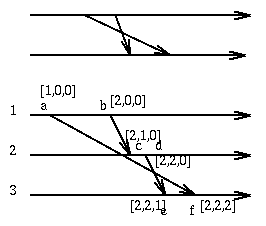
Algorithms are available for converting a messaging system
without the FIFO property into one where the property is satisfied.
In the example above we see that the message
at event f on machine 3 has timestamp [1,0,0] while the last event e
on machine 3 had timestamp [2,2,1]. Thus we know that the message received
at f was sent before the sending of the message received at e.
This does not help us directly since by now the message at e has been
accepted. But if we require that all messages be broadcast, then each machine
will be able to detect if a message is received out of order as shown
in the following graph
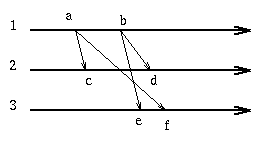
now the message at e is received with timestamp [2,0,0] while the local
clock is [0,0,0] thus we know that an event on machine 1 that
preceded the sending of this message was not received on machine 3.
Consequently we can postpone at machine 3 the delivery of the e message
until after the f event has occurred.
Note that TCP assures the FIFO property on a single connection, but not across
multiple connections. For example A starts a connection with B and
a connection with C. B starts a connection with C. A sends u to B then v
to C then w to B. B sends u to C and then w to C. v could arrive at C
before both u and w, or after both u and w
(or, of courses, in between u and w). In any case, u and w are received in the
correct order both at B and at C.
Physical Clocks
Universal Coordinated Time (UTC) is the standard used for time, based on an
atomic clock. There are radio stations that transmit a pulse each UTC second.
At receivers the accuracy is about 10ms, to account for errors in the transmitter and
mutability in atmospheric conditions. Some computers are with UTC receivers and they can
transmit time information on the internet to other computers.
Given a computer that has a local physical clock that has drift d (i.e., it will
have a maximum error d after one second), if we want it to have an error
betweek the clock of two machines that is
never greater than e, we can do it by requesting a UTC time server for the correct time
every e/2d seconds (the factor 2 accounts for the fact that the drift can slow down
or speed up the local physical clock).
The Christian's Algorithm implements this idea. Here are two potential problems with this algorithm, together with their solution.
- The UTC time delivered to a computer may be smaller than the local time. We cannot reset the local time to the lower UTC since then certain times would be repeated (this
would be a big problem for logs). We deal with this by slowingappropriately the local
clock.
- The UTC time that is received is incorrect because of propagation delay in the delivery of the signal, and because of the overhead in processing the signal. Since
we know the Round Trip Time to+from the server (from the local clock), we can adjust
appropriately the received UTC time.
A number of other algorithms are used for computing synchronized physical clocks. They are based on various forms of averaging between the times held by various computers and on the use of time servers.
The are an unlimited number of uses for synchronized physical clocks and for logical clocks. Among them,
- For physical clocks: at-most-once message delivery and clock-based cache consistency,
(see Tanenbaum, pg 132)
- For logical clocks: scheduling, deadlock prevention, and
consistent checkpoints.





