CIS 307: Precedence Graphs, Concurrency Grain, Fork and Join, CoBegin CoEnd

These topics are not treated in Tanenbaum

This discussion is at the same level of abstraction as our discussion of Activities and Interleaving. That is, we examine a conceptualization that applies not only to software, but to hardware and to organizational processes.

Precedence Graphs

 A PRECEDENCE GRAPH is a directed, acyclic graph where nodes represent sequential activities and where arcs, say from node i to node j, require that activity i complete before activity j can start.

A node in a precedence graph could be a software task, as recognised by the operating system, or could be statements within a program that can be executed concurrently with respect to each other [see example below], or could describe some activity taking place during the execution of a single machine instruction. People refer to the different "sizes" of these concurrent activities, as the CONCURRENCY GRAIN of the representation. It goes from COARSE (the concurrency of operating systems task), to fine (the concurrency of single instructions, or of groups of instructions, as done for example in superscalar processors), to very fine (concurrency in the hardware during the execution of the single instruction).

EXAMPLE 1: Suppose we are given the following sequential program: 
	a := x + y;	/* Statement s1 */
	b := z + 1;	/* Statement s2 */
	c := a - b;	/* Statement s3 */
	w := c + 1;	/* Statement s4 */
	d := a + e;	/* Statement s5 */
	w := w * d;	/* Statement s6 */
We can use the Bernstein conditions to derive a precedence graph from this sequential program. The nodes in this graph are the statements s1, s2, s3, s4, s5, s6. 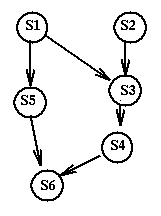This precedence graph could be executed using two processors. One processor could execute in order s1, s5, s6 and the other s2, s3, s4. Of course they should synchronize so that s3 executes after s1 and s6 after s4.This precedence graph is MAXIMALLY PARALLEL for the given program. That is, the only dependencies that appear in the graph are those required by the logic of the program.

Given a precedence graph, how many processors should be used to execute it?

  • Certainly we can execute the graph using a single processor, but in this case we may not exploit the parallelism inherent in the graph.
  • Certainly at most we can use as many processors as there are nodes in the graph. But then, after a processor completes the activity represented by its node, it becomes idle and it is not used efficiently.
  • The maximum number of processors that can be used efficiently is equal to the cardinality of the largest set of nodes such that there is no dependency between any two nodes in the set. [I know you want to prove this! At least try some examples.]
    • Notice the precedence graphs are acyclic, that is, they do not have loops. Thus they cannot represent cyclic computations. Since many of the computations in operating systems are cyclical, this is a strong restriction. There are two ways out. One, represent each cycle with an acyclic graph; you will lose possible concurrency across two successive cycles, but you will be able to deal fully with concurrency within a single cycle. Two, give up on precedence graphs and use instead Petri Nets (unfortunately Petri Nets are beyond the scope of our course).

    We now we examine how we can represent concurrency and precedence graphs using textual representations. We introduce some of the constructs suggested for the specification of concurrency.

    Fork and Join
    FORK and JOIN were introduced in 1966 by Dennis and VanHorne. Though Fork has the same name as an operation in Unix, you should think of them as totally unrelated.

    When the statement:

    Fork(label);
    is executed by a thread of control, a second thread of control is started from the statement with the specified label. The two threads execute concurrently.

    When the statement:

    Join(count);
    is executed, where count is an integer variable, the value of count is decremented. If the resulting value is positive the executing thread is terminated.

    Here are some example where we translate Precedence Graphs into programs using the Fork and Join constructs.
    Note that Fork and Join are Complete for Precedence Graphs in the sense that any Precedence Graph can be expresed using Fork and Join and this is done without loss of concurrency [remember that any precedence graph could be executed as a sequential program, but at a loss in concurrency.]

    CoBegin CoEnd

     The CoBebin Coend construct (also called the ParBegin ParEnd construct) was introduced by Dijkstra in 1968. It is much easier to use than Fork and Join. But, in the sense that we will discuss later, it is not as powerful.

    Here is the construct, where S1, S2, .. Sn are statements:

    When CoBegin is executed, S1, S2, .. Sn are executed concurrently each in a separate thread. When all these statements are terminated, only then the CoEnd is executed and the construct is terminated.

    Here are examples of Precedence Graphs represented using CoBegin CoEnd. Notice that Cobegin Coend is not complete. That is there are Precedence Graphs that can be represented using CoBegin CoEnd only at the cost of some loss in concurrency.

    ingargiola.cis.temple.edu