CIS 307: Introduction to Distributed Systems II

[Distributed vs. Centralized], [Logical Clocks], [Vector Clocks], [Global State], [Mutual Exclusion with a Manager], [No Manager: Ricart-Agrawala Algorithm], [Mutual Exclusion on a ring], [Failure and Recovery], [The two (loyal) Generals Problem]

These notes address material covered in Chapter 11 of Tanenbaum's textbook[only pages up to 490].

Distributed vs. Centralized

In distributed systems we lose a nice property of time: its unique unambiguous value for all participants in communication. In a distributed system different computers may have different clock times. We also lose our tools for supporting mutual exclusion, spinlocks and semaphores cease to work because they use shared memory. A third thing that we lose is the notion of a shared global state. Think of the ready queue, it was a shared object that kept track of all the ready processes in a system - it now has to be distributed. Think of the information used in deadlocks, say, for the Banker's algorithm. In the following we will describe ways to deal with the clock and mutual exclusion problems.

In discussing algorithms in a distributed environment we can distinguish 2+1 cases:

Centralized Solution
There is a "central" node, a manager, that keeps the important information and makes all decisions. Of course, if this node fails we are in trouble.
Distributed Solution
There is no "central" node. Instead:
  • All nodes have approximately the same kinds and amounts of information
  • All nodes decide using the information that is local to them
  • All nodes share responsibility for the final decision
  • All nodes spend about the the amount of resources in arriving at a decision
  • Failure of a node does not cause system's failure
    • Centralized Solution with Recovery
    Here we still have a central decision maker but procedures are in place for recovery in case it fails, in particular for electing a new manager.

    Logical Clocks

    We would like to order the events occurring in a distributed system in such a way as to reflect their possible causal connections. Certainly if an event A happens before an even B, then A cannot have been caused by B. In this situation we cannot say that A caused B, but we cannot exclude that it might have influenced it. We want to characterize this "happened-before" relation on events. We will consider only two kinds of events, the sending of a message and the receiving of a message.

    1. If events e1 and e2 occur in the same system and e1 occurs before e2 (there is no problem to determine this in a single system) then e1 happened-before e2, written e1 -> e2
    2. If event e1 is the sending of a message and e2 is the receiving of that message, then e1 happened-before e2
    3. If e1 -> e2 and e2 -> e3 then e1 -> e3

    The -> relation is a partial order. Given events e1 and e2 it is not true that either they are the same or one happened-before the other. Events that are not ordered by happened-before are said to be concurrent.

    This characterization of happened-before is unsatisfactory since, given two events, it is not immediate (think of the time it takes to evaluate a transitive relation) to determine if one happened before the other or if they are concurrent. We could like a clock C that applied to an event returns a number so that the following holds:

    (1) If e1 -> e2 then C(e1) < C(e2)

    We can define one such C, a logical clock, as follows:

    1. On each computer i we start with a clock Li set at 0
    2. If e is the sending of a message, then increment the local clock Li, set C(e) to Li and timestamp the message with Li
    3. If e is the receiving of a message with timestamp t, then set the local clock and C(e) to max{t, Li+1}
    [We could have started the local clocks with their values set to the same value greater or equal to 0 and using as increments, instead of 1, any value greater than 0. The resulting time still would satisfy (1)] Here is an example showing events a,b,c,d,e,f,g,h,i,j and the corresponding local clocks:

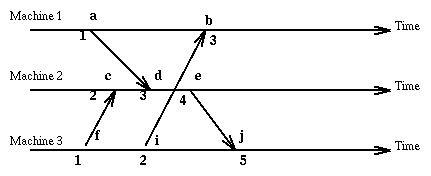
    Since the method we have chosen allows different events (on different machines) to have the same logical clock value, we extent the clock value with a number representing the machine where the event occurred [i, C(e)] and order these pairs according to the rule:

    [i,C(e1)] < [j,C(e2)] iff C(e1) < C(e2) or [C(e1)=C(e2) and i<j]

    Here is an example showing the same events but now tagged with numbers that totally order them:

    Vector Clocks

    A problem of the logical clocks considered above is that they do not represent faithfully the happened-before relation. Namely, it is not true that

    (2) If C(e1) < C(e2) then e1 -> e2

    It would be nice to have logical clocks that would allow us to answer precisely questions of concurrency and dependency. We can do it by using clock values that are vectors of numbers, one for each computer system and then comparing vector values v and u with the rule

    u < v iff ((for all components i, u[i]is less or equal to v[i]) and (there is a j such u[j]<v[j]))

    Here are the rules on vector clocks in a system with n computers:
    1. Each computer starts with a local clock set at [0,0,..,0]
    2. When on computer i there is a sending event, increment the ith component of the clock by 1 leaving other components unchanged, then tag both the event and the message with this value
    3. When on computer i there is a receiving event, first increment the ith component of the clock by 1 leaving the other components unchanged, then form a new local clock value taking the componentwise maximum of the local clock and the time stamp on the arrivimg message. Finally tag the event with this value.

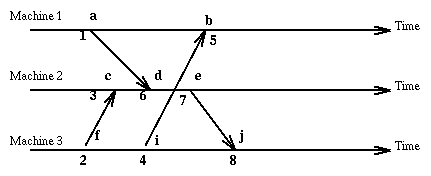
    Here is our old example using vector clock values.

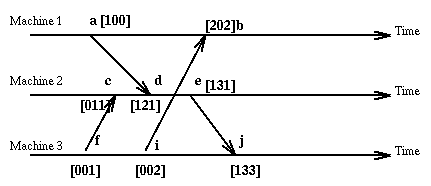
    Of course nothing is perfect. So the use of vector clocks results in big time stamps and requires that we know in advance the identities of the sites involved.

    Global State

    The issues in this section are only food for thought. There will be no questions about them [you may read about them in M.Singhal,N.Shivaratri:Advanced Concepts in operating Systems (McGraw-Hill)]

    I am on a computer system and I want to transfer $100 to your account. So I reduce my account by $100 and send you a message announcing the deposit. When you receive the message, you increment your balance. But during the time the message is in transit by looking simultaneously to your account and my account we find that they are painting the wrong picture. That is, the states that are visible in the two different systems should be as if no message were ever in transit. [Another way of saying this would be to say that the withdrawal/deposit should form an atomic transaction.] If we call local state the content of variables at a site (i.e. its state), global state a vector with as components the local states in the distributed system being considered, and consistency between two distinct local states the fact that the corresponding sites do not have messages in transit, then a consistent global state is one whose component local states are pairwise consistent. For many applications it would be desireable to do things so that the global state is consistent. Equally desireable is to be able to record successive consistent global states (think of debugging).

    Mutual Exclusion with a Manager

    We are given n sites P1 ... Pn that want to use in mutual exclusion a resource R. The requirements of mutual exclusion, progress, fairness, etc. apply now as they did when we were talking about processes. But now there is no shared memory to support spinlocks and semaphores. One easy way of dealing with the problem is to have a Manager Process [or Coordinator] M to whom to send requests and from whom the clients receive permission.

    Here is how a client would operate 

        ..........
    Send request to M
    Wait for reply from M
    Use resource R
    Send release notice to M
    ..........
    This means that each use of the resource will have as overhead 3 messages. If W is the time we use the resource and T is the time taken by each message then the total time spent for a critical region is (W+3T) and the maximum rate of use of the resource is 1/(W+3T). Of course W/(W+3T) is the maximum utilization possible for the resource.

    Now we look at what is done by the manager M: 

        It uses two variables:
      resourceIsFree, a boolean indicating state of resource, initially true;
      rqueue, a FIFO queue containing pending requests;

    loop {
      wait for a message;
      if the message is a request {
        if resourceIsFree {
	  allocate resource to requestor;
          set resourceIsFree to false;
        } else
	  insert request in rqueue;
      } else /* it is a release */
        if rqueue is empty 
	  set resourceIsFree to true;
        else {
	  remove a request from rqueue;
	  send reply to that requestor;}        
    }
    Of course we are in trouble if the Manager dies. Firstly we do not know its current state (i.e., the state of the resource and who is waiting), second, we don't have a coordinator anymore. For the second problem we hold an election to select new manager. For the first problem, each process has to recognise failure and adjust accordingly [each process knows its own state and can communicate it to the new manager].

    No Manager: Ricart-Agrawala Algorithm

    We now consider the problem of mutual exclusion in the fully distributed case where there is no Manager. Instead, we assume that we have n processes, possibly at different sites, P1, P2, ..,Pn. Each process when it needs the resource sends a request to the other (n-1) processes; when it receives (n-1) replies, it goes on to using the resource. When a process is done with the resource it sends a message to all the processes that are waiting for the resource. [This solution assumes a reliable mechanism for delivering messages.] For each use of the critical region it requires 2*(n-1) messages. Thus if the messages are delivered serially we have [W is time spent in a single critical region; T is transmission time for a message]:

    Throughput = 1/(W+2*(n-1)*T); Utilization = W/(W+2*(n-1)*T)

    and if messages were all delivered in parallel

    Throughput = 1/(W+2*T); Utilization = W/(W+2*T)

    Each process must be written to include two threads of control. One to deal with the communication activities, the other to carry out the computations of this process.

    Variables

        self: the identity of this process (a number like 7);
    localClock: an integer representing a local logical clock (initially 0);
    highestClock: an integer, the largest clock value seen in a request
	(initially 0);
    need: an integer representing number of replies needed before self
	can enter the critical region;
    pending: a boolean array with n entries; entry k (k!=self) is true 
        iff process Pk has made a request and process self has not responded;
	the self entry is true if process self wants to enter critical region;
    s: a blocking semaphore used to hold the processing thread while the
	comunication thread takes care of synchronization.

    Communication Thread

      loop {
    wait for a message;
    if the message is a request {
      let k be the identity of requestor and c the clock on message;
      set highestClock to max(highestClock, c);
      if (pending[self] and ([self,localClock] < [k, c]))
	set pending[k] to true;
      else 
	send response to k;
    } else {  /* the message is a reply */
      decrement need by 1;
      if need is 0 
        V(s);}
  }

    Processing Thread

        set pending[self] to true;
    set localClock to highestClock + 1;
    set need to n-1;
    send to all other processes a request stamped with [self, localClock];
    P(s);
    CRITICAL REGION
    set pending[self] to false;
    for k from 1 to n {
      if pending[k] {
	send response to k;
        set pending[k] to false;}
    This algorithm, due to Ricart-Agrawala has been extended by Raymond to the case where more that 1 process can be in the critical region at one time and to the case where requests are for multiple copies of a resource.

    Mutual Exclusion on a ring

    We assume that the communication topology between the processes is a ring, i.e. process Pi can only communicate directly by writing to P(i+1)modn and by reading from P(i-1modn). We assume also that there is a special unique packet, called token, circulating in the ring. A process can enter the critical region only if it is holding the token at this time. Then by its own nature this is a good way of enforcing mutual exclusion in a fair way. There are problems: a node may fail and the ring must be restructured; a token may be lost and we need to elect a node to create a new token. In the case of multiple resources one will use multiple tokens, and different tokens for different kinds of resources.

    In the case that we do not have a ring communication topology, we can still accomplish achieve mutual exclusion using the concept of token. The algorithm is due to Chandy.

    We have n processes P1, .., Pn. The token contains a vector [T1,..,Tn] where Ti is the number of times that process Pi has been in the critical region. Each process Pi has the variables:

    Again Pi is structured as two threads:

    Communication Thread

        loop {
      wait for a message;
      P(mutex);
      if (withToken is true){ 
	 if (clock on stamp is not less than on token) {
           send token to requestor;
	   set withToken to false;}
         /* else the message is discarded */
      } else {
         insert it into rqueue;}
      V(mutex);
    }

    Processing Thread

          .................
      send request time stamped [i,mi] to all other processes;
      wait for token;
      CRITICAL REGION
      set mi in token to mi+1;
      set Ti to mi;
      P(mutex);
      while rqueue is not empty {
	dequeue a request, say, time stamped [j, mj];
	if mj < Tj {
	  it is a stale request; throw it away;
	} else {
	send toKen to Pj;
      }
      if token was not sent out 
         set withToken to true;
      V(mutex);
      .................

    Failure and Recovery

    Failure can occur at nodes and at links. How do we know that a failure has occurred? In the case of nodes there may be messages sent at regular intervals by current site to other site asking Are you there? or messages sent by other site to current site saying I am here. And on messages we may have timeouts.

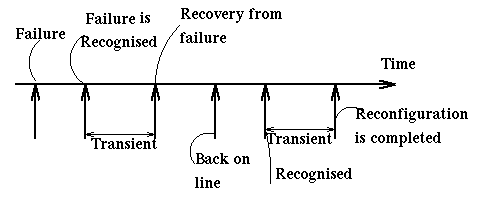
    The following figure shows the time relations between the time of failure, the time the failure is recognized, and the time when the system has reconfigured itself to deal with the failure. The time between the recognition of failure and the completion of reconfiguration is a transient. We have a transient also when a node comes back on line and the system has to reconfigure itself. Things can get exciting (i.e. dangerous) when the two transients overlap.

    The two (loyal) Generals Problem

    Can two sites reach an agreement on when to do simultaneously some action, if we assume that the sites are reliable, they have perfect clocks, but the communication channel between them is unreliable? This problem can be reformulated as follows:
    Two generals with two armies are besieging a city, each on the opposite side of the city. They have very good clocks. They communicate by messengers that may be killed on the way. The generals need to agree on a time when to attack simultaneously the city. If they attack separately, they will lose. If together they will win.
    [The problem is called of the "loyal" generals to distinguish it from the case where there are mamy generals and some of them are traitors sending misinformation, the case of the "Bizantine generals".]

    We can reason as follows with generals A and B. A sends a message to B suggesting "attack at 7am". When A receives agreement from B, it attacks at 7am. The problem is, how does B know that A has received agreement? he cannot thus he does not attack at 7am. So may be A on receiving agreement from B it sends an acknowledgement to B. But then A will not know if B has received the acknowledgement and it will not attack at 7am. There is no solution with a finite sequence of messages. If there were, the last general to send a message would not know if the other general has received that message. Thus that last message cannot be necessary for the agreement, thus the sequence was not minimal. Contradiction. Loyal generals, in the case of unreliable communication cannot reach absolute certainty on when to attack.

    ingargiola.cis.temple.edu