CIS307: SECURITY

Read Chapter 7 in Kurose-Ross's book and pages 554..563 in Tannenbaum.

Security Threats can occur to data, hardware, software, and communication links. Examples of security threats are interruptions (with loss of data, denial of service), interceptions, modifications, fabrications. Of course we aim for Secure Systems, with properties such as:

secrecy (privacy, confidentiality, no eavesdropping),
integrity (no data tampering),
authentication (nobody masquerades as somebody else - spoofing if joe@doe signs in as jane@smith - misrepresentation if www.pinco.com responds to www.ibm.com. A particular kind of masquerading attack is called man-in-the-middle, whereby an interlocutor or principal, places itself between client and server, passing back and forth messages, after registering them and possibly modifying them),
non-repudiation (nobody denies its actions),
authorization (making sure that a principal is allowed to do what it wants to do, using mechanisms such as Access Control Matrices, capabilities, encryption, filtering, firewalls),
auditing (audit-trail = analizable history of use; it establishes a basis for accountability), and
availability, reliability, safety.

We will focus on the first three properties.

In considering security we need to distinguish what are the security policies supported and what are the security mechanisms used to carry out the policies.

Some of the mechanisms involve:

Cryptography, i.e. encoding information so that only the intended interlocutors understand the transmitted information
Message Digests, i.e. hash values computed from the message that almost uniquely identify the message.

Examples of higher level mechanisms are:

Digital Signatures, i.e. encoded message digests used to authenticate the sender and verify the integrity of messages. A digital signature is specific to a message.
Certificate Authority(CA), i.e. an organization that creates and administers the distribution and use of Digital certificates.
Digital Certificates, i.e. data files that act like an online passport for an internet interlocutor (people, web servers, ..). They are issued by a trusted third party, a Certificate Authority, which verifies the identity of the certificate's holder. They cannot be forged. Digital certificates have two purposes: to certificate their holder, and to protect the data exchanged with that holder. A data certificate is specific to a principal, though a principal may have a number of different digital certificates. You may hear these days of support for e-commerce of wallets, that is components that in addition to the information needed for a certificate, they have the information needed for the use of credit cards, plus shipping information, etc.
Public Key Infrastructure (PKI), i.e. the definition of the technical, operational, and legal aspects of using a public key system to provide authentication, access control, confidentiality, and non-repudiation.
Trusted Third party (TTP), i.e. a certificate authority, a public key infrastructure, a higher authority that is agreed to and trusted by the communicating parties.
Internet Messaging Security Mechanisms, i.e. mechanisms such as the Secure Sockets Layer (SSL), a secure extension for MIME, S-Mime, and a secure extension of HTTP, S-HTTP. There is also a Secure Electronic Transactions (SET) protocol and infrastructure for bank card payments over the Internet (developed by Visa, MasterCard, etc.).

CRYPTOGRAPHY

SENDER -->message-->ENCRYPT-->encrypted-->DECRYPT-->message-->RECEIVER

message = plaintext

encrypted = cyphertext

C = E(M), E: encryption algorithm, M: Message, C: Encrypted form of message
M = D(C), D: decryption algorithm
Since good en/decryption algorithm are hard to find, and can be stolen, people find it best to use keys in the algorithm, so that if a key is stolen, one can choose another key, without having to invent, implement, distribute a new algorithm. So the algorithm is public (not private) and the key is private (for now). When using keys, it is usual to write the encoding/decoding as follows:
C = E(M, Ke), M = D(C, Kd) Ke: encryption key, Kd: decryption key

One-way function: a function that is easy to compute but difficult to invert: F(X) is easy to compute with result Y, but given Y is very difficult to determine X such that F(X) is Y.

The key can be private (also called secret) or public. If private only one program knows it. If public, any program can obtain it, usually from an appropriate service. The longer the key, the safer it is. Suppose that I use a key that is just one bit. It is either 0 or 1; it will not take a malicious listener long before the key is guessed!

An encryption/decription schema is symmetric if the same key is used for encryption and for decryption. [To be precise, en/decryption is symmetric if there is a well defined known function for converting between the encryption and decryption key.] It is asymmetric otherwise. Usually symmetric algorithms are much faster than asymmetric algorithms. Often one uses asymmetric cryptography to obtain a key for symmetric cryptography; this key, called a session key, remains valid only for one communication session.

Data Encryption Standard (DES) - secret key, symmetric. Uses 64 bit keys (56 of information plus parity bits). It encrypts/decrypts data in chunks that are 64 bit long. Other sizes often used in DES are 128 (112 of information) and 192 (168 of information). As the size of the key grows, the difficulty of breaking the code grows, exponentially.

Diffie-Hellman (1976) introduced the concept of public keys. [Apparently, in 1973 Clifford Cocks in England came up with the same concept.] If two interlocutors want to talk we will have a Sender and a Receiver. The Sender will find out from a "reliable source" the public key used by Receiver and encode the message with that key. Only the intended receiver will know the private key and decode the message. [To answer the Receiver will have to use the public key of the Sender.]

Rivest-Shamir-Adleman (RSA) (1978)

	D = E, i.e. same algorithm for encryption and decryption
	Ke is public, so we call it Kp
	Kd is secret, so we call it Ks
	----------------------------------
	Choose two primes p and q, let N = p*q
	We will be able to send only messages whose numeric code is < N
	Choose an integer e relatively prime to (p-1)*(q-1) = Z.
	Find the smallest integer d such that
		(d*e)mod Z = 1
	Then the public key Kp is [e,N] and the private key Ks is [d,N].
		     e
		C = M   mod N   //This says that the message M must be smaller
                                //than N. If longer, break it up into 
				//chunks smaller than N and encrypt them 
				//individually.
		     d
		M = C   mod N
        Apparently, given N and e, it is computationally hard to compute d,
        if N is sufficiently large [al least 512 bits]. p and q must each
	be more than 200 bits.
	----------------------------------
	Example: p = 13, q = 17, N = 13*17 = 221, Z = (p-1)(q-1) = 192
		 e = 5
		 d = 77
		 The number of bits we can encrypt is 7 since
		 2^7 = 128 < Z = 192.
		 So if we want to send a message longer than
		 7 bits we will decompose it in 7 bit fragments
		 and encrypt them individually. 
	----------------------------------
	Secrecy: Principal A wants to send a secret message M to principal
	B. [It is usual in the security area to use names like Alice and
	Bob for the principals involved in the interaction.] 
        Let Kp(B) be the public key of B, Ks(B) the secret key of B.
	A will send E(M, Kp(B)). B is the only one with
	Ks(B), thus it is the only one who can read the message. 

		A  -----------------> B
                      E(M, Kp(B))
	----------------------------------
	Authentication: Principal A wants to authenticate itself 
        to other principals. Let Kp(A) be the public key of A, Ks(A) the 
        secret key of A.
	A will append E(A_id, Ks(A)) to its messages. 
	Any principal B that receives this information will use Kp(A)
	to decode the signature, if it succeeds and finds "A_id",
	it will know that only A could have sent the message.
	In the following we use "+" to express "concatenation".

		A  -------------------------> B
		     A_id + E(A_id, Ks(A))
        Note that this authentication, as it stands,  is dangerous: somebody 
        could capture and save that message (A_id+E(A_id,Ks(A))), and then use
        it to impersonate A.

Proof of RSA, Abridged from a report by Sarah Flannery, Blarney, Co. Cork, Ireland

Notation: (a, b) means the greatest divisor of a and b; a | b means that a divides b evenly.

The RSA scheme works as follows

Start Up: [This need be done only once.]

Generate at random two prime numbers p and q of 100 digits or more.
Calculate n = pq and z = (p-1)(q-1).
Generate at random a number e < z such that (e, z) = 1.
Calculate the multiplicative inverse, d, of e (mod z) using the Euclidean algorithm, that is, choose d such that
de = 1 mod z.

Publish: Make public the enciphering key,

	K_E = [n, e]

Keep Secret: Conceal the deciphering key,

	K_D = [n, d]

Enciphering: The enciphering transformation is, for a message M

	C = f(M) = M^e (mod n)

Deciphering: The deciphering transformation is,

	M = f^-1(C) = C^d (mod n)

Why the deciphering works:

The correctness of the deciphering algorithm is based on the following result due to Euler, which is a generalisation of what is known as Fermat's little theorem. This Euler result states that,

	a^z = 1 (mod n)

whenever (a, n) = 1. z, seen a s a function of n, is called Euler's totient function. It is the number of positive integers less than n which are relatively prime to n.

When n is a prime p, z is p - 1, and we have Fermat's little theorem:

	a^p-1 = 1 (mod p) ; (a, p) = 1

If p|a then a^p = a = 0 (mod p), so that for any a,

	a^p = a (mod p)

Now since d is the multiplicative inverse of e, we have

	ed = 1 (mod z) => ed = 1 + k*z, for some integer k.

Now

	f^-1(f(M)) = (M^e)^d = M^ed (mod n)

and

	M^ed = M^1+k*z (mod n)      (for some integer k)

Now for M with (M, p) = 1, we have

	M^p-1 = 1 (mod p) => M^k*z+1 =
	M*M^{k*(p-1)*(q-1)} = M*(M^p-1)^k*(q-1) = M (mod p)

This is trivially true when M = 0 (mod p), so that for all M, we have

	M^ed = M^1+k*z = M (mod p)

Arguing similarly for q, we have for all M,

	M^ed = M^1+k*z = M (mod q)

Since p and q are relatively prime, together these equations imply that for all M,

	M^ed = M^1+k*z = M (mod n).

[addedum]In fact

	M^ed = M (mod p) => M^ed> - M = K1 * p
	M^ed = M (mod q) => M^ed> - M = K1 * q

thus K1*p = K2*q. Since p and q are primes, K1 must be equal to K3*p*q. Which is all we need to show.

The RSA algorithm is not good for protecting large messages since with it encryption/decryption are fairly slow - more that 1000 slower than DES. But it can be used to transmit essential information, such as secret keys and passwords. [Apparently on a 175Mhz Alpha RSA encrypts 1kbps, while 56-bit DES encodes over 30Mbps.] In RSA it is normal to use 512-bit and 1024-bit keys.

The Key distribution problem for public and private keys is dealt with through a Public Key Infrastructure and the use of digital certificates.

One-Time Pad

There is a an encryption method that is unbreakable, but very inconvenient. Suppose that we know that we need to send from A to B a message of n bits. We give before hand to both A and B a pad string s of n bits randomly generated. Then A will encrypt his message M as M^s, where ^ means exclusive or. And B will decrypt the encrypted message E with E^s. The trick is that, take a message bit x and a pad bit y, we have

x^y^y = x

Try it for any of the values of x and y and you will see it is true.

DIGITAL SIGNATURES and DIGEST FUNCTIONS (Integrity)

User A writes a document M, wants to distribute it and be sure that

all receivers R are sure that the document is the unmodified original one (integrity, no tampering),
it has been sent by A (no impersonation), and
A cannot deny having sent it (non-repudiation).

A does not care who or how many principals(programs/people) read the message.

Digest Function: a function that, given a document M generates a brief "fingerprint" or "message digest" or "hash value" or "thumbprint" that identifies this document uniquely with almost certainty.

MD5 (Rivest, 1992): A digest function that generates a 128 bit fingerprint from its text argument. It is much quicker to compute than encrypting with DES [on a 175Mhz Alpha, MD5 digest is computed at over 80Mbps].

A sends:

	M + E(MD5(M), Ks(A))    // Ks(A) = Secret key of A

['+' means concatenation, E(MD5(M), Ks(A)) is called the digital signature of the message. It is also often called a Message Authentication Code (MAC).]
R uses the identifier of A to determine the public key of A.
R uses this public key of A to decrypt the "digital signature" of M and obtain the hash value MD5(M).
R uses the Digest Function to compute the hash value of M.
If the two hash values are the same, all is well. Otherwise message was corrupted or not sent by A.
[A possible weakness of the MD5 algorithm has been discovered and a replacement has been suggested (dobertin).]

	A  ----------------------> B
	    M + E(MD5(M), Ks(A))

A weakness of the use of digital signatures is that it requires knowledge of the public key of the interlocutors. The danger is impersonation - if there is no reliable way of distributing public keys. The solution, as we will see later, is to use digital certificates and certificate authorities.

Direct Authentication: Client-Server

We want a client to authenticate its identity to the server and the server to authenticate its identity to the client. We assume that the true client and server share a secret password P from which an algorithm can compute a key K. We use the notation K(Client) and K(Server) to indicate the value of K as assumed respectively by the client and the server. We should have K = K(Client) = K(Server). [Instead of a protocol based on symmetric cryptography, we could have used a protocol based on asymmetryc cryptography.]

The client selects at random an integer x [it is random so that likely it was not used before and nobody can remember previous exchanges] and sends to the server the message
```
         clientId + E(x, K(Client))  
```
The server uses K(Server) to decode E(x, K(Client)) and determine the value of x.
The server selects at random a number y and sends to the client the message
```
	E(x+1, K(Server)) + E(y, K(Server))
```
The client uses K(Client) to decode the message received. At this point, if x+1 was retrieved, the client is certain of the identity of the server. Now the client sends to the server the message
```
	E(y+1, K(Client))
```
The server uses K(Server) to decode the message. If y+1 was retrieved, the server is certain of the identity of the client.
The server sends to the client the message
```
	E(SK, K(Server))
```
SK is the session key that the server and client can use to exchange information during this session. Note that only the specified client will be able to decode the session key. This session key will be valid only for a specified time interval. The fact that K is used only during the exchange that results in the sharing of the session key SK, makes it more difficult for an hostile party to guess K.

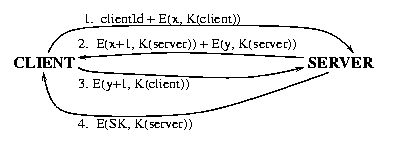
The values x and y are usually called nonces. They are just computed random numbers. As already observed, they are used so that an intruder cannot imitate an interlocutor by just remembering what that interlocutor returned in another occasion.

Authentication Server

Authentication protocol (modified from a protocol by Needham - Schroeder) used when there is an Authentication Authority S. It is carried out when a Client A wants to communicate with a server B. It is assumed that the authentication server and A share a secret key K(A) and the authentication server and B share a secret key K(B). Usually these secret keys are computed from userid, password pairs.

A sends to S the cleartext message
```
	A + B
```
to mean that A wants to interact with B.
S generates a timestamp T, a duration L (Lifetime), and a session key K and sends to A the message:
```
	E(T + L + K + B, K(A)) + E(T + L + K + A, K(B))
```
Now A uses its key K(A) to obtain the session key K, plus T and L; it then sends to B the message
```
	E(T + L + K + A, K(B)) + E(A + T, K)
```
B uses K(B) to determine T, L, K and A. The E(A + T, K) part is necessary to authenticate that the message is really from A (only A can have obtained the session key K, as demonstrated by the A+T value) and not from somebody that eavesdropped the conversion between S and A and obtained the E(T + L + K + A, K(B)) part. For this reason the E(A+T,K) part is called an authenticator. Now also B has the session key K, plus T and L, and knows that it can interact with A. It does so by sending to A the message
```
	E(T+1, K)
```
to indicate that B is ready. This authenticates B to A since only B has the session key K, as demonstrated by T+1.

More About Digital Certificates, Certificate Authorities, and SSL

As already indicated, a digital certificate is associated with an internet interlocutor to make secure its interactions with other interlocutors. At a minimum a digital certificate will include:

Name and Digital certificate of the certification authority that issued this certificate
The name and the public key of the owner of the certificate
Serial number and expiration date of the certificate.

In addition it may contain also the owner's address, e-mail address, phone, etc. The certificate is encoded by the issuing certificate authority using its private key so that the content of the certificate cannot be tampered with without detection. Here is how the certificate works. The sender requests the certificate of the recipient from the CA. This certificate is encrypted with the CA's secret key and contains the recipients's public key and additional information. The sender decodes the certificate with the public key of the CA and encodes the message with the retrieved public key of the receiver. The standard for Digital Certificates is X.509.]
A message M can be sent as follows:

	M + DigitalSignatureOfM + DigitalCertificateOfSender

and, if the certification authority is reliable, we are guaranteed authentication and non-tampering. Thus digital certificates can be used in place of passwords to identify principals.

A Certificate Authority, in addition to issuing certificates, will be concerned with renewing (i.e. extend the duration), and revoking (i.e. terminating the validity) existing certificates. A Certificate Authority cannot appear as a single server to which all users make appeal. Instead, as in the case of DSN (Distributed Name Service) one needs a distributed structure of communicating certificate authorities. At present there are a number of competing certificate authority services and a server used in e-commerce will have to keep certificates for the certification services it trusts. Front ends to certificate authorities are often called Registration Authorities.

SSL, the Secure Socket Layer, acts as an intermediate layer between the application protocol, say HTTP, and the transport protocol, say TCP. SSL has two subprotocols. One specifies the format of the messages exchanged. The other specifies the handshakes taking place between clients and servers. The protocol allows the selection of the cryptographic algorithm used. It always requires authentication of the server. Authentication of the client is optional. [Server authentication is almost always crucial - think of client having to give to server its own visa card number. Client authentication is rarer - necessary, for instance, if client asks for bank balance; not necessary if client asks for today's weather. In the case that the client gives a credit card number, the application using SSL will have other methods to make sure that the client is who it claims to be.]

In their SSL interactions interlocutors use digital signatures, digital certificates, and rely on certificate authorities. They use random numbers (nonces) to eliminate the possibility of hostile interlocutors remembering old interactions. Communications between client and server are encrypted. Public key cryptography is used only during session setup: the client, usually a browser, selects a secret symmetric session key, encrypts it with the public key of the server, and sends it to the server. Afterwards client and server communicate with the selected secret session key.