Transactions

[This topic is presented in pages 271-288 in Tannenbaum - VanSteen.]

What is a Transaction

Transactions are mainly studied in the context of [distributed] data bases, but the concept is a model on how to implement reliable [distributed] applications. Often people refer to the desired properties of transactions using the ACID acronym:

Atomicity: All or none behavior.
Consistency: Each transaction is correct, that is, it preserves the invariants of the system (things like "the sum of all credits and debits is zero"); the concurrent execution of transactions also preserves the invariants of the system.
Isolation: Intermediate results during execution are invisible. This is like saying that the effect of the concurrent execution of transactions is equivalent to their serial execution (thus, also called Serializability).
Durability: the effect of a transaction that completes successfully is persistent.

As we will see below, isolation is achieved by using serializable schedules (usually, two-phase locking); durability is achieved by saving results in persistent store; consistency is required of the people that develop the transactions, at the application, not at the tool level [a money transfer transaction should worry about preserving accounting rules, not the system - however, if the invariant is formally specified, the system will fail transactions that violate the invariant]; and atomicity is achieved in two steps, first in single systems (usually with logs), then in distributed systems (usually with the two-phase commit protocol).

Transactions are easy to use. A Transaction Server will support operations to Start a Transaction and to End a Transaction. The termination of a transaction can take two forms: success, called commit, and failure, called abort. Abort gives up on the current transaction. Many are the reasons for aborting a transaction. They range from the internal logic of the transaction (like making reservations for a multi leg trip and then giving up in the middle when a particular leg cannot be scheduled) to crashes occurring in one of the systems taking part in a distributed transaction. When a transaction commits or aborts, many house-keeping action will be required to complete ("close the books" on) the transaction. The Transaction Server will worry about how to guaranty transactionality for the actions performed between the Start and End delimiters. It is a "service" provided to us without need for us to program anything: it is both valuable and free.

The concept "transaction" is fundamental in our discipline. It takes a number of operations and executes them atomically, without any worry about potential concurrent activities. As the systems of the future will have a multitude of processors and people confront the fact that concurrent programming with threads and locks is hard and error prone, alternatives are sought. Transactions offer an alternative way of dealing with concurrency. Already people have been working on Software Transactional Memory [STM]. It is likely to be influential in the future.

We have from the beginning of the course worried about the concurrent execution of activities, their possible interleavings (or schedules), about mutual exclusion, and critical sections. Here we examine a number of undesirable behaviors caused by interleavings that violate the ACID properties. These interleavings lead to transaction aborts.

Lost Updates: Account 1 has 1000 dollars - the actions A and B represent two deposits to this account):

   A1: Read value of Account 1         
   A2: Add 100 Dollars to it      
                                         B1: Read value of Account 1
                                         B2: Add 1000 Dollars to it
                                         B3: Store value in Account 1
   A3: Store value in Account 1

This interleaving results in a balance of 1100 dollars and not 2100 dollars as it should be.

Inconsistent Retrieval: Consider the following two sequences of actions performed by two different processes (we assume that initially Account 1 has 1000 dollars and Account 2 has 2000 dollars - The first sequence of actions represents the transfer of 100 dollars from Account 1 to Account 2; The second sequence of actions represents a report on the balances of these accounts):

  A1: Read value of Account 1 
  A2: Subtract 100 dollars from it
  A3: Store value in Account 1 
                                         B1: Read value of Account 1
                                         B2: Print this value
                                         B3: Read value of Account 2
                                         B4: Print this value
  A4: Read value of Account 2    
  A5: Add 100 dollars to it
  A6: Store value in Account 2

This interleaving will result in the apparent disappearence of 100 dollars.

Dirty Reads (i.e. reading an uncommitted value):

   A0: Start	
   A1: Read value of Account 1 (say 100)
   A2: Add 10 to it	
   A3: Store value in Account 1
                               		B0: Start
	                                B1: Read value of Account 1
		                        B2: Add 5 to it
		                        B3: Store value in Account 1
					B4: End
   A4: Abort

The problem in this interleaving is that B uses a value updated by a transaction that has not yet been committed. This situation should never occur, since B is committed, yet it should be aborted because it uses the results of the aborted A transaction. This is a form of cascaded abort.

Premature Writes(i.e. writing an uncommitted value):
```
   A0: Start
   A1: Read value of Account 1 (say 100)
   A2: Add 10 to it
					B0: Start
					B1: Read value of Account 1
   A3: Store value in Account 1
					B2: Add 5 to it
					B3: Store value in Account 1
					B4: Abort
   A4: End
```
The problem in this interleaving is that when the B transaction aborts, it re-establishes the initial value of the account, thus wiping out the effect of the A transaction. Thus, if we get in trouble as in the Dirty Read and Premature Writes, we need to abort also the other transaction (B in Dirty Read, A in Premature Writes). This is again a form of cascading aborts.

If transactions are executed one after the other [this is called a serial schedule], we avoid the aberrations that are caused by their concurrent execution on shared data. But by doing so the response time in executing the transactions becomes excessive, more than users will tolerate. Fortunately not all is lost: to avoid aberrations it is not necessary to have serial schedules, serializable schedules will suffice: a serializable schedule is a schedule that is equivalent to a serial schedule on the basis of the Bernstein's Conditions. This requires some thought and explanation.

Serializability of Transactions

The operations we carry out in a transaction are not all created equal. Since a transaction is an all or nothing affair, we need to know, if we give up in the middle of a transaction, waht operations need to be undone. Some operations, for instance on temporaries, need not be undone. Let's call them unprotected operations. Others are read or write operations to our store, they need to be undone, and we call them protected. Finally there are operations that operate on the real world and cannot be undone, like printing message, or giving out money at an ATM, and we call them real operations. We exclude real operations like input from a user since such operations make for long-lived transactions which are hard if not impossible to have satisfy the ACID properties. So we dismiss the unprotected operations, we postpone the real operation until a decision has been made on committing, and we worry only about the protected operations. In some cases together with the definition of a transaction one defines a compensating transactions, i.e. a transaction whose purpose is to undo the effects of the original transaction fully or partially completed.

Let's use the notation W(a) to indicate a write operation on object a and R(b) to indicate a read operation on object b. Let S be the start of a transaction, A is the Abort, and C is the Commit. In describing transaction Ti, let's append an i to its S, A, C, R and W operations, say, Si, Ai, Ci, Wi(a), and Ri(b). For the time being let's postpone consideration of S, C, and A operations, focusing only on R and W. Two operations that operate on the same object are said to be conflicting operations if they are not both read operations. This reflects what we know from the Bernstein's conditions. Conflicting operations cannot be reordered.

Now let's consider some transactions:

   T1:  R1(a) R1(b) W1(a)
   T2:  R2(b) R2(a) W2(b)

and the schedule ("schedule" is another name for "interleaving")H1:

   H1:  R1(a) R1(b) R2(b) W1(a) R2(a) W2(b)

[For the time being we do not worry about locking any item.] Since R2(b) and W1(a) operate on different objects, their order could be changed without affecting the result when executing H1. Thus we would get the schedule H2:

   H2:  R1(a) R1(b) W1(a) R2(b) R2(a) W2(b)

which is just the serial execution of T1 followed by T2. In this case we say that the schedule H1 is serializable. Of course not all schedules are serializable. For example the schedule H3:

   H3: R1(a) R1(b) R2(b) R2(a) W1(a) W2(b)

is not serializable since R2(a)W1(a) cannot be reordered as W1(a)R2(a) since the values for a used in T2 in the two cases are different. [This is basically what was said with the Bernstein's conditions.] And also R1(b)W2(b) cannot be reordered for the same reason.

We have a general way to determine if a schedule is serializable. Suppose that we have a schedule of transactions T1, T2, .., Tn. We create a serialization graph with nodes T1, T2, .., Tn. We then put an arc from node Ti to node Tj (and we say Ti precedes Tj) if we find in the schedule an Ri(x) before a Wj(x) or a Wi(x) before an Rj(x) or a Wj(x). Notice that these operations will have to be protected by read or write locks and Ti will have to release the lock on x before Tj can acquire the lock on x. [Our discussion of conflicting operations and serializability, is a simplification of reality. The order of read and write operations on the same object by different transactions has to be preserved - for example R1(x)..W2(x) must be kept in this order as does W1(x)..R2(x). But when considering write operations to one object without intervening reads, only the last write matters. For example,W1(x)W2(x)W1(x) is equivalent to W2(x)W1(x)W1(x) since the effect of these operations depends only on the last W1(x).]

Serializability Theorem: A schedule is serializable if and only if its serialization graph is acyclic.

But this theorem is not easy to apply: it is not reasonable to expect that transactions will be executed while checking at all times that no loop occurs in their serialization graph.

Two-Phase Locking

We use locks (read locks and write locks as necessary) to prevent undesired schedules. We denote a locking operation with L and unlocking with U. We assume that the context makes it clear what are read locks and what are write locks. We assume that no read or write operation takes place on an object without the appropriate locks being in place on that object.
[Things can be made more complicated: we may have a system where we may first read lock an item, and later on raise that lock to a write lock. Alternatively, we may start with a write lock on an item, and then demote that to a read lock for that item. Raises will have to take place during the locking phase, and demotions during the unlocking phase. ]

We will say that a transaction follows a Two-phase Locking [2PL] Policy if it never applies a lock after having released a lock. The first phase is when we apply locks, the second phase is when we release them.

Theorem: If transactions follow the two-phase locking policy then schedules that respect the locks and don't deadlock, are serializable. Viceversa schedules that are not serializable will deadlock.

We examine only the case of two transactions, T₁ and T₂ that have conflicting operations on objects a and b. Without loss of generality we can assume that the first operation is by T1 on a. We have cases

  1.  a1   b1 // then a2 and b2 in some order - serializable with no deadlock
  2.  a1   a2 // then T2 will block until T1 is done - serializable with no deadlock
  3.  a1   b2 // now no matter the order of a2 and b1, - non serializable, with deadlock

Two problems remain when using two-phase locking:

As we have seen, it is possible that the two-phase locking policy will result in a deadlock. For example if we are given the transactions [L stands for Lock, U stands for Unlock]
```
   T1:   L1(x) W1(x) L1(y) W1(y) U1(x) U1(y) 
   T2:   L2(y) W2(y) L2(x) W2(x) U2(y) U2(x) 
```
we can create the schedule
```
   L1(x) W1(x) L2(y) W2(y) L1(y) L2(x) ...
```
that is two-phase locking and results in deadlock when T1 executes L1(y) and T2 executes L2(x).
Notice also that the use of two-phase locking does not guaranty that there will be no cascading aborts. Let's now add Start, Commit, and Abort operations. Given the transactions
```
   T1: S1 L1(x) W1(x) U1(x) A1
   T2: S2 L2(x) R2(x) W2(x) U2(x) ..
```
the two-phase locking policy will allow the schedule
```
   S1 L1(x) S2 W1(x) U1(x) L2(x) R2(x) W2(x) U2(x) A1 ..
```
which will require a cascaded abort A2 after T1 aborts.
Cascading aborts can be fully prevented if a transaction does not release any write lock until the transaction is completed (committed or aborted: strict 2-phase locking [S2PL]). This is a policy that results in decreased concurrency and increased delays. Yet the complication of having to deal with cascading aborts is such that strict scheduling is usually adopted. In these notes, unless otherwise indicated, we will assume strict scheduling.

Lock management is usually not a programmer's concern. Locks can be inserted automatically by the system to enforce a desired policy. For example, if we have transaction T:

   S R(x) R(y) W(x) W(y) R(z) W(u) C
then locks can be inserted as follows [using 2PL]:
   S L(x) R(x) L(y) R(y) W(x) L(z) L(u) U(x) W(y) U(y) R(z) U(z) W(u) U(u) C
or, better, [using S2PL]:
   S L(x) R(x) L(y) R(y) W(x) W(y) L(z) R(z) L(u) W(u) C U(z) U(x)
U(y) U(u)

Serialization by using Timestamps

There is an alternative to the use of locks, with consequent possibility of deadlock: by using timestamps. Suppose that each object is timestamped with the start time ST(T) of the last transaction T to access that object. Then a transaction T will abort if it accesses an object that has a timestamp later than the start time of T. This is bad if these aborts occur frequently, but if rare, this technique is fine. This way of executing transactions, where transactions access shared objects in the same order as the transactions were started, is called the Strict Execution of Transactions policy.
This method has a problem if used in a distributed system: how to guarantee that the timestamps really reflect the true ordering of transaction start times. This will be discussed when we study clocks.

The use of timestamps to serialize transactions can be refined. Assume that to each object X we associate two timestamps.
W-timestamp WTS(X) is the start timestamp of the transaction that wrote last successfully to X. Similarly R-timestamp RTS(X) is the latest start timestamp among the transactions that have read successfully from X.
When transaction T wants to read from X, if ST(T) is less than WST(X), T is aborted. Otherwise it succeeds and RTS(X) is set to the largest of RTS(X) and ST(T).
When transaction T wants to write to X, if ST(T) is less than the RTS(X) or less than the WTS(X), T is aborted. Otherwise it succeeds, the write is executed and the WTS(X) is set to the start timestamp of T.
Notice that the timestamps on an object X are monotonically increasing.
For example, the refinement in the use of timestamps allows the following interleaving to complete successfully, which would not have been possible with the simple use of timestamp introduced earlier [transaction 1 would have aborted at 4]:

	Transaction 1	        Transaction 2   R-timestamp     W-timestamp
	1  Start                                0               0
				2  Start
				3  read X       2
	4  read X                               2
				5  write X                      2
	6  write Y                                              1 (of Y)
	7  Commit
				8  Commit

Atomic Transactions

We are left with a fundamental problem of transactions: atomicity. We need to examine how to deal with failure, aborts, commits.

Atomic transactions on a single system

We consider first the case where a single computer is involved in a transaction. Usually the data is maintaned in a database (we could also have flat files) under the control of a database manager (DM) (in this context it is often called just resource manager). Since reading from disk is slow and since synchronous writes to disk are very slow, all sorts of buffering schemes and caches are used. Thus write operations to persistent storage will have to be done in the correct order and, unless one is careful, data will be lost in case of system crashes.

A number of implementation strategies are possible. Among them:

WriteAhead Log - Redo-Only, also called Deferred-Update
We assume we have in stable storage a writeahead log (also called a Redo Log, or a Database Log, or an Intentions List), it is just a sequential file. Initially all the operations are done acquiring locks without modifying the data base, just writing to the log for each transaction a start record and for each update command the command and the data that has to be written to complete the operation. [Note the record will include the indentifier of the transaction and it will be an indempotent write operation: if we had 100 in an account and we withdraw 10, the write operations says to write 90 to the account.]
When all this information has been logged (this phase is called the precommit phase) a commit record is written to the log. Anything of the transaction that was done before this commit, in the case of failure, is discarded and we are as if back to before the beginning of the transaction. After the commit, the transaction will be completed on the real data, not the log, because we have in the log all the information needed to carry it out and we are holding all the needed locks. This method of implementing the transaction is called redo-only because when we commit we need to redo each (update) operation of the transaction (if we give up we need not do anything to the database). The locks that were acquired in the precommit phase, are held throughout the redo phase. Here is what is done in correspondence to the various operations of a transaction:
- StartTransaction: Write a new transaction record to the WriteAhead Log.
- Write (or Update): Write a Redo Record to the WriteAhead Log. This record contains the id of the transaction, the identity of the variable being updated and the value being written.
- Read: Now we need to check if the variable to be read has already been updated in the transaction, thus we have to combine the information in the WriteAhead Log with what is in the database or, better, we can keep the updated object in the cache until the transaction is committed and the new value written to persistent memory. The read operation does not affect the log.
- Abort: release locks and discard the WriteAhead Log of this transaction (and the updated objects from the cache).
- Commit: After all log writes are completed, write to log the commit record. Then (redo phase) apply to the database in order the actions in the WriteAhead Log, from newest to oldest, but only one write per variable [i.e. if we had logged a number of writes to variable x, then only the last write needs to be redone]. The write a transaction completed entry to the log.
  Example: We have integer objects x, y, z, and w with respectively values 1, 2, 3, and 4. A transaction writes 6 to x, 7 to y, 8 to x, 9 to z, 10 to y, and 11 to w. In the log we will have, from oldest to newest, without recording the transaction id:
```
		variable  newValue
		==================
		x		6
		y		7
		x		8
		z		9
		y		10
		w		11
```
  Now we commit the transaction. Then in order, while the locks are being held, we write in the database 11 to w, 10 to y, 9 to z, and 8 to x. The older writes to x and y are not done since we have already updated these variables with more recent values. Then the locks are released, the transaction is completed (becomes inactive) and a transaction completed record is written to the log. Notice that in the commit phase we only do write operations and that the order in which we do them within a transaction is immaterial (the writes are all to distinct objects). Thus scheduling of these operations can be done so as to improve efficiency.
  Notice also that in case of a crash if it happens before the commit record, as we can see by looking at the log, the transaction is discarded. If it happens after the commit, but before the completed record, the write operations of the transaction are carried out [we need not worry about locks if recovery is done in a non-concurrent mode]. Crashes after the completed record do not affect that transaction.
WriteAhead Log - Undo-Only, also called Update-in-Place
An alternative is to have a precommit phase where we apply locks and for each update command we save to the WriteAhead Log (now called Undo Log) the data that will be modified (so that we can undo the command) and we execute on the real database the command. We then write a commit record to the log. Here is what is done in correspondence to the various operations of a transaction:
- StartTransaction: Write a new transaction record to the Undo Log.
- Write (or Update): Write an Undo Record to the Undo Log. This record contains the id of the transaction, the identity of the variable being updated, its old value and new value. Then write the new value to the data base. The Undo Record must be on disk before the new value is written to the DB.
- Read: Just read the value from the data base. It does not affect the log.
  Example: Again we have integer objects x, y, z, and w with respectively values 1, 2, 3, and 4. A transaction writes 6 to x, 7 to y, 8 to x, 9 to z, 10 to y, and 11 to w. In the log we will have, from oldest to newest, without recording the transaction id
```
		variable  oldValue	newValue
		================================
		x		1	6
		y		2	7
		x		6	8
		z		3	9
		y		7	10
		w		4	11
```
- Abort: Write the Abort record to the log. Carry out the undo operations in the order they were done, but only one undo per variable [i.e., if variable x was written a number of times, we need to reinstated only the oldest value of x]. In our example, while the locks are being held, we write in the database 1 to x, 2 to y, 3 to z, and 4 to 4. The newer writes to x and y are not undone since we have already restored these variables to their original values. The a transaction completed record is written.
- Commit: Just write to disk a commit record for the transaction. Do not discard yet the log: since non-synchronous writes can take many seconds to be fully recorded in persistent storage, when we write the commit records, the writes to the data may not have yet been completed. Thus in case of crash the data would be lost. Wait for the transaction to become inactive (say, after a sufficient number of seconds) before discarding log.
If there is a crash, in the recovery we undo all the active aborted transactions and we redo all the active committed transactions. We need to redo the active committed transactions because though the log entries are already on disk, there is no guaranty that the data updates are on disk. We can do what is needed because we have on disk the needed information (old and new data) for both redo and undo.
Private Workspace
This is an interesting idea already encountered in Copy-On-Write (COW) fork operations and in Write-Once file systems. The idea is to give to each user its own copy of the data being updated, but this copy is just a directory of the blocks affected (the blocks may come from many files). Then when the update is made by a transaction to a block, it is written to a new block (called a shadow block) and the directory of that transaction is updated to point to this new block. When all updates are carried out and the new directory is copied to a log in stable storage together with a commit record, the transaction is ready to be completed by updating atomically the real directories of the database. Notice that in case of failure before commit we do not need to do anything to the database, just update lists of free blocks since blocks allocated to the aborted transactions can be recovered.

All logs are kept in stable storage. For each transaction we will have a start transaction record and an end transaction record. Then space for the log can be recovered by compaction after freeing the space associated to completed transactions, or by treating the log as a circular tape where we restart from the beginning after having reached the end. Notice that logs, since they are sequential files, they allow fast processing. Information is logged at much greater speed than if it were actually recorded in a large store.

Restart and Checkpoints in a Single System

Restart is the operation required after a system failure. The restart operation will take care of the transactions that were not completely done at the time of the crash. Aborted transactions are undone, committed transactions are completed, and uncommitted transactions are undone.

Checkpoints (i.e. the saving of intermediate values of objects during a transaction) can be used to reduce the amount of work to be done during restart for undo-only logging. Checkpointing consists of three phases:

Be sure that all incompleted writes to the log are completed
Write a checkpoint record to the log.

In the case of restart we need only consider the incomplete transactions and the transactions that were started after the most recent checkpoint.

Atomic Transactions in a Distributed System

The problem is the following: A number of systems are involved in executing a transaction. One is the transaction manager or coordinator, usually it is the system where the transaction was started. All systems have a resource manager that operates as indicated above for transactions on single systems. A resource manager is responsible for carrying out the local operations keeping a local log and, in addition, for communicating with the (transaction) manager. We assume that communication is reliable and we accept the fact that any system may fail and recover. Each system has available stable storage to record reliably their progress and decisions across temporary local failures and recoveries. A system will record to the log (stable storage) its state before sending messages so that if it fails when it recovers it can resend the message and continue with the transaction. If fail-recover time does not violate communication deadlines, then it will be treated by all as a communication delay. We want to reach the situation where all systems complete in agreement that the transaction is committed or that it is aborted. If committed the transaction should be fully completed. If aborted all the systems should go back to the state they were in before the transaction started. Of course the agreement should be faithful to the truth: there is commitment iff all systems will complete their tasks. A solution is provided by the Two-Phase Commit Protocol.

   Part 1:
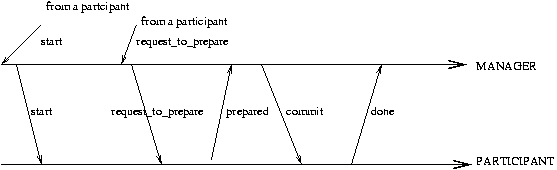
      The transaction(a program in the transaction) starts by informing 
      the transaction manager (or coordinator) that will write to 
      stable storage a StartTransaction record and inform all participant 
      resource managers (also called participants).
      Now the transaction is Active and all participants are in the
      working state.
      Carry out the operations of the transaction at each system
      as we did in the pre-commit phase in the single system transaction.
      [We are holding locks.]

    Agreement Protocol:
      At this point all the operations of the transaction have been
      carried out in a "non-committed" fashion holding locks. A program in 
      the transaction issues the "REQUEST_TO_PREPARE" request to the transaction manager. 
      Phase 1:
        The manager writes a pre-commit record to the log (stable storage)
        and sends to all participating resource managers the request that 
        they report their decision to commit or abort (REQUEST-TO-PREPARE). 
        A resource manager that receives this request moves 
        into the prepared state.
        The resource manager writes a pre-commit or abort record to
        the log (stable storage) and reports to the coordinator
        its local decision to commit (PREPARED message) or abort
	(NO message). 
        The coordinator collects the answers [if any is late, it is
        assumed to be an abort] then decides to commit iff
        all replies were to commit. The decision is recorded
        in stable storage at the coordinator with a commit record
        At this point, if commit was chosen, the transaction is 
        "committed": it must be brought to a successful conclusion.
      Phase 2:
        The coordinator informs all participants of the decision with
        a COMMIT or ABORT message. 
	Now the participants must
        carry out that decision. 
	[The coordinator 
        will send at intervals the decision until it 
        receives a DONE message from all participants.]
        When a participant receives the commit message, it transits to the
	committed state.
        A participant will acknowledge with a DONE message a received commit
        or abort message so that the coordinator can stop overseeing this
        participant and release resources it may be holding.


    Part 2:
      The actions are finalized at all systems. This can be accomplished
      reliably since what to do is recorder in stable storage
      at each site. The participant record the completion of the
      transaction in their log and the transaction becomes Inactive.

Note that people think of the two phases as referring to Part 1 and Part 2, while in reality the two phases refer to the two rounds of the agreement protocol. The agreement protocol requires 4(n-1) messages, where n is the number of systems. Notice that the transaction manager has to write to stable storage during the transaction the starttransaction information, then the prepared message, then either the committed or aborted message (at a later time it can write that the transaction is inactive). Thus 3 synchronous writes are required, i.e a transaction will take more than 10 milliseconds to complete, independently of any communication delays.
A transaction can be in one of the following states:

working: From the start of the transaction to the start of the two-phase protocol.
prepared: During the two-phase protocol.
Committed or Aborted: After the two-phase commit protocol before the completion of the transaction.
Inactive: All participants have finalized the transaction.
The transaction is active when in any state but the inactive state.

The following picture display the interactions between the coordinator and a participant during a transaction.

The two-phase commit protocol is imperfect since it assumes that no system will fail permanently.

Consider the case that a participant j fails permanently after phase 1 when all had agreed to commit. Then the coordinator decides to commit and informs the others but the transaction cannot complete since system j is not there to accept the message from the coordinator and acknowledge it, and the coordinator cannot abort because by now some systems may have finalized their action. The transaction remains in the uncertain state and becomes blocked. Some extraordinary action must be taken, usually in the form of a compensating transaction that undoes or somehow fixes the previous transaction.
It is a greater problem if the coordinator fails permanently at the end of phase one, just before informing the participants of its decision. The participants that have failed will know what to do [abort, thus re-establishing the previous state], but those that had decided to commit are in trouble [they are left hanging on how to finalize the transaction, i.e. they are blocked] and the transaction remains in the uncertain state. These blocked systems will attempt to reach resolution by sending queries to the coordinator requesting disposition information for the incomplete transaction.

So some additional work, not part of the two-phase commit protocol, needs to be done to handle these problems. Basically, we need to have some way of knowing when we can close the books on a transaction and say that it is done. A three-phase commit protocol has been suggested to deal with the weaknesses of the two-phase protocol.

Impossibility of Guarantieing Consensus in Asynchronous Systems

The problems encountered in the Two-Phase Commit Protocol (the blocking of the transaction) is an example of a general problem: our inability to guarantee arriving at a consensus in a system where

messages are reliable,
the execution and communication times of systems are not with known upper bounds
one system may fail.

Because of this impossibility, one aims not to guaranty consensus, but to minimize the probability of failing to achieve consensus. Also, one aims to establish emergency procedures for handling failures.

Transaction Servers

One takes advantage of the services provided by the Transaction Server and need not worry about concurrency control and recovery. The system (transaction server) will take care of that, locking and unlocking as required. Thus transaction processing represents a "higher level" form of programming. Of course, somebody has to implement such a transaction server and support its functionality. It should not be surprising to find out that transaction servers are complex and that transactions have a high overhead. People evaluate the performance of many kinds of distributed systems on the basis of the number of transactions they can support in a unit of time.

Nested Transactions

In some systems it is possible to define nested transactions, that is transactions defined within other transactions. An abort in a nested transaction terminates the nested transaction only, not the containing transaction. For example a transaction could be:

	A0: Start
	A1: Something
	A2: Start
	A3: Something
	A4: Abort
	A5: Start
	A6: Something
	A7: End
	A8: Something
	A9: End
is equivalent to just A0, A1, A5, A6, A7, A8, A9.