CIS 4307: INTERLEAVING, DETERMINATE COMPUTATIONS, BERNSTEIN CONDITIONS, PRECEDENCE GRAPHS

Operating Systems support Tasks (or Processes). But for now let's think of "Actitivities". Activities are more general than processes, since they may be expressed by software, or hardware, or even by what people do. They consist of sequential atomic actions (an atomic action executes in an all-or-nothing mode, with invisible intermediate states, with a well defined behavior). [Atomic actions are also called operations. - We can think of the Read/Load instruction from physical memory as an atomic operation, and the same for Write/Store; we will see the need for instructions that are atomic and involve both Load and Store to memory, but for simplicity our atomic operations will usually be just read or write.]

[WARNING: When we execute the instructions of a program in a computer we believe that they will be executed on the memory sequentially, one after the other, in the same order as in the program [called program order]. In reality, though the (single-ported) memory executes operations in sequence, it is possible that the processor may reorder some operations so as to speed up execution. [A processor where the instruction and memory ops are executed in program order are called with in-order execution, and with out-of-order execution otherwise.] For example, on x86 architectures the sequence: store 1 to Y; read X into a register may be executed with the read operation first and then the write operation. However operations (read or write) to the same location executed on one processor will be carried out on the memory in that same order. In addition write operations in a multiprocessor with caches may not be atomic, i.e. a write operation may have updated some caches, with reads that in some caches retrieve the new value while in other caches reads retrieve the old value. Special instructions, called barriers of diferent kinds, can be used to ensure that all instructions (may be only reads, or only writes, or both) appearing in a thread before a barrier complete before the barrier is executed, or that all instructions (may be only reads, or only writes, or both) appearing in a thread after a barrier are executed after the barrier has completed, or both, i.e instructions in a thread before the barrier complete before it executes and those after execute after the barrier completes. Implementations of lock and unlock methods include the execution of appropriate barrier operations. Unless explicitly said otherwise we will assume that reordering does not occur and instructions are executed sequentially the way they are written in the program, i.e. the machine satisfies the program order requirement. Of course compilers may for optimization purposes add complexities such as reordering of operations and use of temporary auxiliary variables, which result in problems in multiprocessor systems.]

Activities can be executed in parallel. Here are two activities, P and Q:

        P:      abc
        Q:      def

        abcdef
        abdcef
        abdecf
        abdefc
        adbcef
        ......
        defabc

The importance of the concept of interleaving is that it allows us to express the meaning of concurrent programs: The parallel execution of activities is equivalent to the sequential execution of one of the interleavings of these activities. [This way of interpreting the effect of execution of concurrent programs is one of the possible ways to interpret that effect of executing the program (there are others). Each such interpretation is called a memory consistency model. The model we have chosen is called sequential consistency model. Memory consistency is particularly complex for multiprocessor systems with caches. We will deal somewhat with caches in a future lecture. For people who are interested in memory consistency issues, here are some references - David Mosberger: Memory Consistency Models, S.V.Adve, K.Gharachorloo: Shared Memory Consistency Models. This topic is important if one wants to understand concurrency at the hardware level, and also in Java, as you can see in the Java specification for threads and locks. To simplify our lives as programmers, we hope to operate in systems that satisfy the sequential consistency model. And if we create a platform for other users, we try to make it such that it satisfies sequential consistency. But often performance requirements do not allow it: sequential consistency may be only achievable at substantial performance cost. The topic of consistency is treated in depth in textbook, pages 276-295]

Since concurrent activities can have many interleavings, these interleavings may complete with different results. We will say that a set of activities (i.e. a program) is DETERMINATE if any time it runs, for the same inputs, it gives the same outputs. Otherwise it is NON-DETERMINATE (it has a RACE CONDITION).

Here are two activities that are not determinate. The first activity just executes the assignment a = 1; The second activity just executes the assignment a = 2;

Suppose that you are given the following two activities P and Q:

        P:  x = 2;                     Q:  x = 3;
            y = x - 1;                     y = x + 1;

Here is an example of undesirable interleaving (it has a name: the lost update problem). Consider the following two sequences of operations performed by different processes (we assume that initially Account 1 has 1000 dollars - the sequences represent two deposits to this account):

Here is another example of undesirable interleaving (it also has a name: the inconsistent retrieval problem). Consider the following two sequences of operations performed by two different processes (we assume that initially Account 1 has 1000 dollars and Account 2 has 2000 dollars - The first sequence of operations represents the transfer of 100 dollars from Account 1 to Account 2; The second sequence of operations represents a report on the balances of these accounts):

        x = u + v;
        y = x * w;

If these conditions are not satisfied, then it is still possible that the parallel execution of P and Q is determinate [can you come up with an example?], but usually it is not. [Note: We have discussed these conditions considering only two activities, but as you have guessed they generalize to more activities.]

The Bernstein Conditions are informative but too demanding: in most situations we want to execute activities that read/write the same data, and yet we don't want to give up determinacy. Thus something else is needed, some way of limiting the interleavings that are possible when executing activities in parallel. That is what SYNCHRONIZATION MECHANISMS do for us.

When writing programs in a high level language it is particularly important to understand that the interleavings we have to worry about are not the interleavings of the statements of the high level language. Instead we have to worry about the interleavings of the machine instructions they are compiled into. And, in modern machines with multiple concurrent elements, even about the interleavings taking place at a lower level.

Two interleavings are said to be equivalent if they give the same results. An interleaving, or schedule, is serializable if it is equivalent to a serial schedule. For example, given the activities

   A1: x = 1;            B1: x = 2;
   A2: y = 2;            B2: z = 3;

Consider two activities and two operations in these activities. If these operations do not satisfy the Bernstein's conditions they are said to be conflicting. If we have two interleavings of these activities where two conflicting operations are in reverse order, then the two interleavings will not be equivalent. For example for the activities

   A1: x = 1;            B1: x = 2;
   A2: y = 2;            B2: z = 3;

From what we have said it is clear that the danger is when we have an object accessed by two different activities, at least one access being a write. All such pairs of accesses have to be made non concurrent by using some form of lock.

We need to be careful about what are "atomic operations". Suppose we have two variables x and y initialized respectively to 1 and 2. We have two concurrent activities:

	x = y;				y = x;

	temp1 = y;			temp2 = x;
	x = temp1;			y = temp2;

Precedence Graphs

A node in a precedence graph could be a software task, as recognised by the operating system, or could be statements within a program that can be executed concurrently with respect to each other [see example below], or could describe some activity taking place during the execution of a single machine instruction. People refer to the different "sizes" of these concurrent activities, as the CONCURRENCY GRAIN of the representation. It goes from COARSE (the concurrency of operating systems task), to fine (the concurrency of single instructions, or of groups of instructions, as done for example in superscalar processors), to very fine (concurrency at the register transfer level in the hardware during the execution of the single instruction).

EXAMPLE 1: Suppose we are given the following sequential program:

        a = x + y;     /* Statement s1 */
        b = z + 1;     /* Statement s2 */
        c = a - b;     /* Statement s3 */
        w = c + 1;     /* Statement s4 */
        d = a + e;     /* Statement s5 */
        w = w * d;     /* Statement s6 */

This precedence graph could be executed using two processors. One processor could execute in order s1, s5, s6 and the other s2, s3, s4. Of course they should synchronize so that s3 executes after s1 and s6 after s4.This precedence graph is MAXIMALLY PARALLEL for the given program. That is, the only dependencies that appear in the graph are those required by the logic of the program.

Beware that the optimization that we have achieved in Example 1 by identifying possible concurrency within a sequential program is potentially dangerous. Consider two sequential programs intended to run concurrently, where initially B has value 0:

   Program 1:                Program 2:
      A = some value;           while (B == 0);
      B = 1;                    Read value of A;

Given a precedence graph, how many processors should be used to execute it?

• Certainly we can execute the graph using a single processor, but in this case we may not exploit the parallelism inherent in the graph.
• Certainly at most we can use as many processors as there are nodes in the graph. But then, after a processor completes the activity represented by its node, it becomes idle and it is not used efficiently.
• The maximum number of processors that can be used efficiently is equal to the cardinality of the largest set of nodes such that there is no dependency [i.e. directed path] between any two nodes in the set. [I know you want to prove this! At least try some examples.]

In general, given a precedence graph and given m processors, it becomes important to determine which tasks should be executed on each processor and in which order. If we only are interested in the question of which task is allocated to which processor [usually so that the processors are fairly equally loaded], we talk of Load Balancing. If we are interested in exactly which task runs where and in which order [usually so that the completion of all the tasks happens as early as possible], we talk of Scheduling.

There is a fairly simple way of scheduling (called list scheduling) a precedence graph assuming that all processors are alike. We assign "priorities" to the nodes (i.e. tasks). Then when a processor becomes free, we allocate to it the task with highest priority among the unallocated tasks all of whose predecessors have already terminated. We often use as "priority" of a task its optimal completion time [for each path starting at this node we compute its execution time as the sum of the times of the tasks on the path; we then take the maximum of these values for all the paths starting at this node. Note that this is the time of the critical path starting at this node.]. Note that this algorithm, though often good, does not guaranty optimality. For example in the following precedence graph.

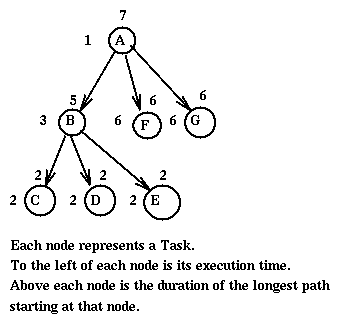
If we have two processors P1 and P2 the algorithm would result in the schedule (Gantt chart)

        1 2 3 4 5 6 7 8 9 0 1 2 3 4
      +-+-+-+-+-+-+-+-+-+-+-+-+-+-+
  P1  |A|F|F|F|F|F|F|B|B|B|C|C|E|E|
      +-+-+-+-+-+-+-+-+-+-+-+-+-+-+
  P2  | |G|G|G|G|G|G| | | |D|D| | |
      +-+-+-+-+-+-+-+-+-+-+-+-+-+-+

        1 2 3 4 5 6 7 8 9 0 1 2 3 4
      +-+-+-+-+-+-+-+-+-+-+-+-+-+-+
  P1  |A|F|F|F|F|F|F|C|C|D|D| | | |
      +-+-+-+-+-+-+-+-+-+-+-+-+-+-+
  P2  | |B|B|B|G|G|G|G|G|G|E|E| | |
      +-+-+-+-+-+-+-+-+-+-+-+-+-+-+

Of course, list scheduling might have worked if we had given different priorities to the nodes. For example, if we use as priority of a node the sum of the execution times of the node and all its successors, [Thus C, D, and E have priority 2. B has priority 9, F and G have priority 6, and A has priority 22.] the schedule we obtain using List Scheduling is optimal.

List scheduling can be described by the algorithm:

    Given a precedence graph and a set of machines:
	Initialize agenda to empty;
	Set all machines to free;
	do {
	   Place all nodes that have no predecessors (and are not already 
                in agenda or executing on a machine) into the agenda;
	   While (the agenda contains nodes and a machine is free)
                Remove a node from agenda, and allocate it to a free machine;
	   When (a machine becomes free) //we receive a signal, or an interrupt
                Remove from precedence graph the node just executed;
	} until (agenda is empty and all machines are free);

The list scheduling algorithm we have seen is an example of an algorithm that requires knowledge about all the machines and activities and that decides in a centralized fashion what to do at all machines. This does not work well in a distributed environment. Often better is to have a way of distributing processes to machines so as to have approximately similar load everywhere - Load Balancing, and then a way to schedule processes at each individual machine.

Notice that the precedence graphs are acyclic, that is, they do not have loops. Thus they cannot represent cyclic computations. Since many of the computations in operating systems are cyclical [for example: wait for some event, respond to it, and then go back to waiting], this is a strong restriction. There are two ways out. One, represent each iteration as an acyclic graph; you will lose possible concurrency across two successive iterations, but you will be able to deal fully with concurrency within a single iteration. Two, give up on precedence graphs and use instead Petri Nets (Petri Nets are beyond the scope of our course). [Another possibility: if you know the number of iterations of the loop, and this number is small, you can unfold the loop into the sequence of iterations, without looping.]