We discuss two seemingly unrelated topics, Group Communication and Data and/or Service Replication. Group communication is often used to achieve Replication. We will not discuss how groups are created and maintained, nor we will worry about possible relations between groups.
In Group Communication, contrary to Point-to-Point Communication, we have one transmitter and many receivers: all the members of the group. A one-to-many message can be realized
A unicast message m involves two events, the sending of the message, s(m), and the reception of the message r(m). In the case of a multicast message m, we have the sending of the message s(m) and, for each node i in the group, the reception of the message at node i, r(m,i). Clearly s(m) -> r(m,i) for all nodes i in the multicast group. We say that a communication system enforces FIFO ordering for messages if for any two messages m1 and m2 sent by the same node we have:
if s(m1) -> s(m2) then for all i in the group r(m1,i) -> r(m2,i)In TCP fragments of a message may be delivevered out of order to the receiver system, but TCP at this system reorders the fragments and delivers them in the right order to the receiver. Thus TCP is with FIFO ordering of the fragments within a message. (And of course TCP is FIFO for successive messages.) TCP can do that since the fragments of the message are stamped with offset information.
We say that a communication system enforces the causal ordering of messages if for any two messages m1 and m2,
if s(m1) -> s(m2) then for all i in the group r(m1,i) -> r(m2,i)If a system enforces causal ordering then it also enforces FIFO ordering, but not viceversa.
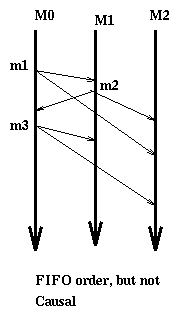It is FIFO since all arrivals of m1 occur before the correspondent
arrivals of m3.
It is not causal since s(m1) happens before s(m2), but r(m2,2) happens
before r(m1,2).
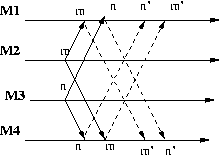
Here is an example of where we have no causal ordering: I send a letter with a deposit to a bank, later I send a letter with a check. The check gets cashed before my deposit is received by the bank. Clearly the mail system does not preserve the causal ordering of messages. We want to delay the delivery of messages that are out of order until all the causally preceding messages have been delivered. Here is an algorithm that enforces causal ordering:
CBCAST Algorithm (ISIS - Birman + Joseph):
We are given nodes M1, M2, .., Mn.
Each node Mi maintains a vector [S1,S2,..,Sn] where Sj indicates that
messages 1, 2, .., Sj have been received from node Mj.
When node Mi sends a message, it will time stamp it with the vector
[S1,..,Si+1,..,Sn].
When node Mj with vector [S1,S2,..,Sn] receives a message from Mi
with time stamp [T1,T2,..,Tn]
1. We accept the message if
(1) Ti = Si+1 and
(2) for all k different from i, Tk <= Sk
Where (1) means that this is the next message from Mi to reach Mj, and
(2) means that the sender does not know more about other machines
than the receiver.
2. We hold and delay the message if
(3) Ti > Si+1 or
(4) Ti = Si+1 and there is a k such that Tk > Sk
Where (3) means that there is an earlier pending message from Mi
and (4) means the sender has received messages not yet delivered to the
receiver.
3. We discard the message if
(5) Ti <= Si
Where (5) means that we are dealing with a duplicate message.
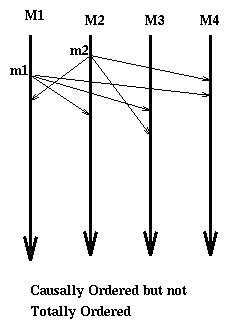
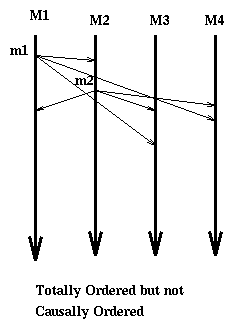
We say that a communication system enforces the total ordering of messages if for any two messages m1 and m2, m1 and m2 are delivered in the same order at all nodes. Note that this definition does not guaranty causal order. In fact in the following diagram we have messages that are trivially causally ordered (since the sending of m1 and of m2 are not ordered) but not totally ordered since some of the arrivals of m1 happen before some arrivals of m2 and some after.
The example said to be totally ordered but not causally ordered it is so since (1) for the machines where there are arrivals from both m1 and m2 we have all the arrivals of m2 before the correspondent arrivals of m1 (total order); but (2) s(m1) happens before s(m2) yet r(m2,3) happens before r(m1,3) (no causal order).
One way of implementing total ordering of messages is to have a sequencer node. Then when a node wants to send a message it first requests a sequence number from the sequencer, then multicasts the message timestamped with that number. Each node keeps track of the highest number received. A message when it is received it is delayed if its sequence number is greater than 1 plus the local number, it is accepted if it is equal to 1 plus the local number, and it is discarded if it is less. The total ordering is also a causal ordering if the reception of the sequence number and the sending of the message marked with that number is done as an indivisible action. [The use of a sequencer brings about all the problems we have seen when discussing the use of a coordinator for mutual exclusion. But distributed solutions (ABCAST algorithm) are so complex and time consuming that they are avoided.]
An even stronger constraint on a communication system than (causal) total ordering is to require that it be ordered, causal, and that the sending of a multicast message from a node be interpreted as the reception of that same message from that node (in other words, all the events associated with a message happen before or all happen after the events associated to another message). Such a system is said to be synchronous. In a synchronous system it is as if the sending and delivery of a message were instantaneous and we can divide time at each machine at intervals demarked by the sending/delivery of messages.
Data and/or processing power may be replicated at a number of sites for a number of reasons:
ingargio@joda.cis.temple.edu