CIS 307: Deadlocks

[Introduction], [Resource Allocation Graphs], [Deadlock Prevention], [Deadlock Avoidance], [Deadlock Detection]

Deadlocks in distributed systems are treated in Tanenbaum, pages 158 through 166. Here is some material reviewing deadlocks in general. Tanenbaum must be read and learned together with this note.

Introduction

Deadlock occurs when we have a set of processes [not necessarily all the processes in the system], each holding some resources, each requesting some resources, and none of them is able to obtain what it needs, i.e. to make progress. We will usually reason in terms of resources R1, R2, .., Rm and processes P1, P2, .., Pn. A process Pi that is waiting for some currently unavailable resource is said to be blocked.

Resources can be preemptable or non-preemptable. A resource is preemptable if it can be taken away from the process that is holding it [we can think that the original holder waits, frozen, until the resource is returned to it]. Memory is an example of a preemptable resource. Of course, one may choose to deal with intrinsically preemptable resources as if they were non-preemptable. In our discussion we only consider non-preemptable resources.
Resources can be reusable or consumable. They are reusable if they can be used again after a process is done using them. Memory, printers, tape drives are examples of reusable resources. Consumable resources are resources that can be used only once. For example a message or a signal or an event. If two processes are waiting for a message and one receives it, then the other process remains waiting. To reason about deadlocks when dealing with consumable resources is extremely difficult. Thus we will restrict our discussion to reusable resources.
Resources are usually with a multiplicity, i.e. an indication of how many copies of the resource exist. So we may have 3 tape drives, 2 printers, etc. We normally assume that resources have a multiplicity different than 1. If it were always 1 the study of deadlocks could be simplified. In fact, in the case of data bases, or of shared persistent objects, it is usual to have only a single copy of the object (or if there are many copies, as with replicated objects, their access from one user are so different that we can treat the copies as distinct resources with multiplicity one).

Deadlock can only arise in a system where:

Resources are used in mutual exclusion,
Resources are acquired piecemeal (i.e. not all the resources that are needed to complete an activity are obtained at the same time in a single indivisible action).
Resources are not preempted (i.e. a process does not take away resources being held by another process). And,
Resources are not spontaneously given up by a process until it has satisfied all its outstanding requests for resources (i.e. a process, seing that it cannot obtain some needed resource it does not kindly give up the resources that it is currently holding).

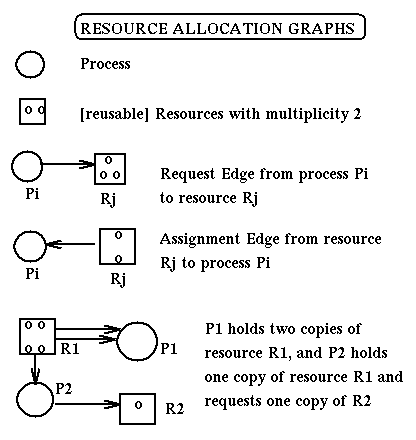
Resource Allocation Graphs

Resource Allocation Graphs (RAGs) are directed labeled graphs used to represent, from the point of view of deadlocks, the current state of a system.

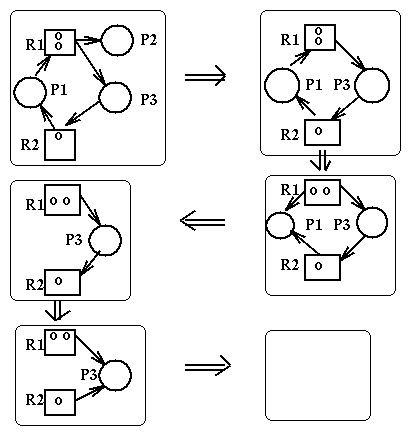
State transitions can be represented as transitions between the corresponding resource allocation graphs. Here are the rules for state transitions:

REQUEST: if process Pi has no outstanding request, it can request simultaneously any number (up to multiplicity) of resources R1, R2, ..Rm. The request is represented by adding appropriate requests edges to the RAG of the current state.
ACQUISITION: if process Pi has outstanding requests and they can all be simultaneously satisfied, then the request edges of these requests are replaced by assignment edges in the RAG of the current state
RELEASE: if process Pi has no outstanding request then it can release any of the resources it is holding, and remove the corrisponding assignment edges from the RAG of the current state.

Here are some important propositions about deadlocks and resource allocation graphs:

If a the RAG of a state of a system is fully reducible (i.e. it can be reduced to a graph without any edges using ACQUISITION and RELEASE operations) then that state is not a deadlock state.
If a state is not a deadlock state then its RAG is fully reducible [this holds only if we are dealing with reusable resources; it is false if we have consumable resources]
A cycle in the RAG of a state is a necessary condition for that being a deadlock state
A cycle in the RAG of a state is a sufficient condition for that being a deadlock state only in the case of reusable resources with multiplicity one.

Here is an example of reduction of a RAG:

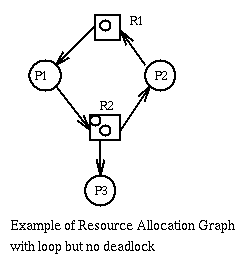
And here is a deadlock-free system with a loop.

Deadlock Prevention

Deadlock Prevention is to use resources in such a way that we cannot get into deadlocks. In real life we may decide that left turns are too dangerous, so we only do right turns. It takes longer to get there but it works. In terms of deadlocks, we may constrain our use of resources so that we do not have to worry about deadlocks. Here we explore this idea with two eaxmples.

Linear Ordering of Resources

Assume that all resources are totally ordered from 1 to r. We may impose the following constraint:

LO: A process cannot request a resource Rk if it is holding a resource Rh with k < h

It is easy to see that with this rule we will not get into deadlocks. [Proof by contradiction.]
Here is an example of how we apply this rule. We are given a process that uses resources ordered as A, B, C, D, E in the following manner:

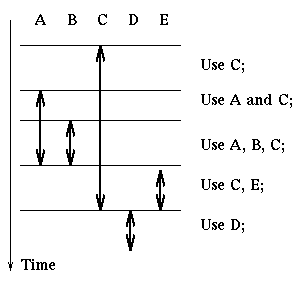
Then the process can do the following:

    acquire(A); acquire(B); acquire(C);
    use C
    use A and C
    use A, B, C
    release(A); release(B); acquire(E);
    use C and E
    release(C); release(E); acquire(D);
    use D
    release(D);

A strategy such as this can be used when we have a few resources. It is easy to apply and does not reduce the degree of concurrency too much.

Hierarchical Ordering of Resources

Another strategy we may use in the case that resources are hierarchically structured is to lock them in hierarchical order. We assume that the resources are organized in a tree (or a forest) representing containment. We can lock any node or group of nodes in the tree. The resources we are interested in are nodes in the tree, usually leaves. Then the following rule will guarantee avoidance of deadlocks.

HO: The nodes currently locked by a process must lay [simultaneously and at all times until the desired resourses are acquired] on all paths from the root to the desired resources.

Here is an example of use of this rule, locking a single resource at a time.

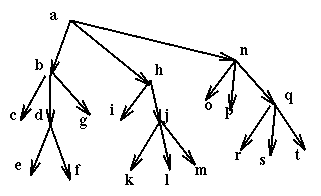
Then if a process wants to use the resources e, f, i, k it uses in sequence the commands:

lock(a); lock(b); lock(h); unlock(a); lock(d); unlock(b); lock(i); lock(j); unlock(h); lock(k); unlock(j); lock(e); lock(f); unlock(d);

Of course by forcing all locking sequences to start at the root of the resource hierarchy we create a bottleneck, since now the root becomes a scarce resource. As always there are trade-offs to be made. An obvious improvement on this prevention policy is to start not by locking the root, but by instead locking the lowest node subsuming all the nodes used by the current activity. For example if we had an activity that accessed only the nodes p, r, and s then we could start by locking n, not a.

Tannenbaum discusses prevention policies for distributed systems: the wait-die policy and the wound-wait policy, both based on the timestamp of competing transactions.

Deadlock Avoidance

Deadlock Avoidance, assuming that we are in a safe state (i.e. a state from which there is a sequence of allocations and releases of resources that allows all processes to terminate) and we are requested certain resources, simulates the allocation of those resources and determines if the resultant state is safe. If it is safe the request is satisfied, otherwise it is delaied until it becomes safe.

The Banker's Algorithm is used to determine if a request can be satisfied. It uses requires knowledge of who are the competing transactions and what are their resource needs. Deadlock avoidance is essentially not used in distributed systems.

Deadlock Detection

Deadlock Detection, in the case where it is available information about the full resource allocation graph, it is easy since there is deadlock if and only if there is a loop in the resource allocation graph. In the case that the multiplicity of resources is 1, we can simplify the detection of deadlocks by building a wait-for graph, i.e a graph where the nodes represent processes and there is an arc from Pi to Pj if there is a resource R that is held by Pj and requested by Pi. The wait-for graph of a system is always smaller than the resource allocation graph of that same system. There is a deadlock in a system if and only if there is a loop in the wait-for graph of that system.

Distributed System Case

It is easy to get into deadlock with transactions that follow two-phase locking and it is easy, if we compute correctly the wait-for graph, to detect a deadlock has occurred. For example, if we have 3 computers 1, 2, and 3, with resources respectively, A, B, and C and D and we have three transactions T1, T2, and T3 that execute as indicate below:

   TRANSACTION T1        TRANSACTION T2         TRANSACTION T3
  (Transfer from B       (Transfer from         (Transfer from A
   to A and D)            C to B)                to C)
  ==============================================================
   Lock(D)
   Deposit to D
                         Lock(B)
                         Deposit to B
   Lock(A)
   Deposit to A
                                                 Lock(C)
                                                 Deposit to C
   Lock(B)
                         Lock(C)
                                                 Lock(A)
  ----------------    Deadlock  --------------------------------
   Withdraw from B       Withdraw from C         Withdraw from A
   Unlock A,B,D          Unlock B,C              Unlock A,C
  ===============================================================

we have the wait-for diagram

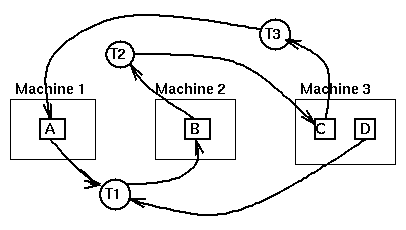
that has a loop, thus we have a deadlock.

As Tanenbaum shows, when the wait-for graph is computed at a central location that collects messages from the various systems involved in transactions, it is easy to find also false, or spurious, or phantom deadlocks as in the following picture

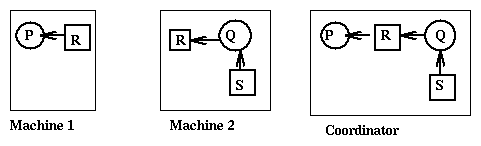
when Q first releases S and then P requests S, but the messages delivered to the coordinator that collects the messages arrive in the wrong order. Then the coordinator believes that a deadlock has arisen and kills unnecessarily P or Q. Of course, if Q was following a 2-phase locking policy, it would not release any lock until it had acquired every lock it needed. Thus phantom deadlocks would not arise if 2-phase locking is followed.

The Chandy-Misra-Haas algorithm detects deadlocks in a distributed system (resources with multiplicity 1) without requiring a coordinator.
When process Pi requests a resource held by process Pj, it sends a message of form

   [Requestor of resource, 
    source of message, 
    destination of message]

to Pj, thus in this case Pi sends to Pj the message [i, i, j]. In turn Pj will send to each process Ph such that Pj requests a resource held by process Ph, the message [i, j, h]. The same will be done by Ph, etc. if the original requestor Pi receives a message of form [i, *, i], then it will know that there is a loop, that a deadlock will arise, thus it will delay the request or abort. For example, here is what happens in the following system when process P1 requests a resource held by process P2:

indicating that a deadlock arises.

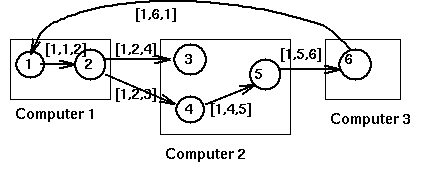
For distributed deadlock prevention can be used timestamps indicating the start of transactions and then ordering priority in case of conflictson the basis of the time stamp. The following diagram describes two deadlock prevention policies:

    WAIT-DIE POLICY           |  WOUND-WAIT POLICY
                              |
    Wants          Holds      |  Wants
    Resource       Resource   |  Resource
    +-------+      +-------+  |  +-------+      +-------+
    |Older  |----->|Newer  |  |  |Older  |----->|Newer  |
    |Transac|      |Transac|  |  |Transac|      |Transac|
    +-------+      +-------+  |  +-------+      +-------+
    It will wait              |  Preempt
                              |
                              |
    Wants          Holds      |  Wants          Holds
    Resource       Resource   |  Resource       Resource
    +-------+      +-------+  |  +-------+      +-------+
    |Newer  |----->|Older  |  |  |Newer  |----->|Older  |
    |Transac|      |Transac|  |  |Transac|      |Transac|
    +-------+      +-------+  |  +-------+      +-------+
    It dies                   |  It will wait