CIS307: Bridges, Routing
A Bridge
is a box with ports (usually two) to LAN segments. It operates in promiscuous mode at the data link layer (i.e. at the level of frames, not signals), it examines all frames and it recognizes where they came from, and where they are going to. It selectively (frame filtering) transfers frames from any port to other ports. It does not propagate noise signals and defective frames as it was the case for repeaters (at the physical layer). It adaptively recognizes which machines are reacheable from a port. It reduces traffic on each port and it improves security since each port will only transmit frames directed to nodes reacheable from that port (thus one does not overhear irrelevant traffic).
Bridges are normally used to connect LAN segments within a limited geographic
area (local bridges), like a building or a campus.
But they are also used in the network of
an enterprise to interconnect LANs: a bridge in a LAN is connected through
some long distance channel (for example, a line provided by a common carrier)
to a bridge in a distant LAN (remote bridges).
Usually bridges connect segments using the same
data link protocol, but some modern bridges can convert between different
data link protocols (for example, ethernet and token ring).
Bridges move packets to the correct physical addresses no matter what is the network
protocol that sent them.
Bridges can be transparent (usually in Ethernet lans),
also called spanning tree bridges,
where the aim is to minimize
all work required to set up a bridge and have instead
the hardware and software set up the bridge with the information
required for routing frames correctly. Thus transparent bridges
are plug-and-play devices, that operate as intended without
the need of operator intervention to set up the system.
Or bridges can be source routing bridges (usually in token ring lans)
where the route from sender to receiver are preset at the sender and
included in the frame.
We will only discuss transparent bridges.
All the nodes reacheable from a node through segments and bridges
will receive broadcast messages sent by that node. They constitute the
broadcast domain of the given node.
Bridges are able to filter frames on the basis of any information available at the data link level in the frame. For example, since an Ethernet frame has a field with information about the higher level protocol used in the data portion of the frame, a bridge could be programmed to filter out frames that use selected protocols.
Though modern routers alleviate the need for bridges by being fairly easy to configure and manage, bridges remain useful and desirable because of their simplicity and high performance.
The algorithm is run independently at each bridge.
It makes the natural assumption: If a frame from a node
j is received through port i then messages to j will go
out through i.
It keeps a cache of pairs of the form [i,j]
where i is a port (of the current bridge) and j
is the address of a node (usually an ethernet address)
reacheable from the current bridge through port i.
This cache is initially empty.
When the bridge receives a frame from a port i it determines the
physical addresses of its source, j, and of its destination, k.
If k is a multicast address, then the frame is forwarded through
all the ports except the one through which it was received
(flooding).
If the pair [i,j] is not already in the cache, it is added to it.
If [i,k] is in the cache then
the frame is discarded.
else if there is a pair [h,k] in the cache then
the frame is forwarded through port h
else
it is forwarded to all ports (flooding) except i.

NOTE: We are representing a LAN as a bus, a line, to which is attached terminal equipment. Then the bridges are nodes connected to two or more LANs. More often than not modern LANs have instead a star configuration with hubs or switches at the center of the star.
This algorithm does not assume any knowledge on the part of a bridge about the structure of the network. It just uses the address information in the frames about senders and receivers. With this information, for example, a message from 3 to 5 will not be forwarded by bridge A. Also, if 2 had also sent a message, then local traffic between nodes 1 and 2 would not be forwarded by either bridge A or B. Since bridges operate below the network layer, they do not us IP addresses, instead addressing is done using physical addresses, for instance ethernet addresses.
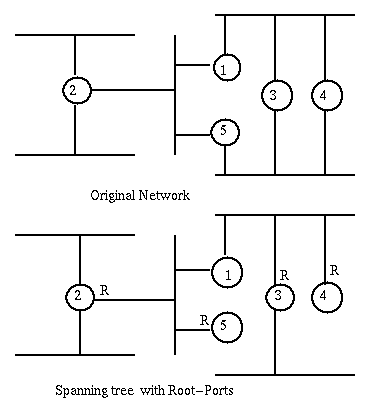
The intent of the Distributed Spanning Tree Algorithm is to identify the node (i.e. bridge) with smallest id, the root-bridge of the network; Then for every other node, to identify the port, root-port, through which goes the shortest path to the root-bridge. Finally for every lan segment to choose the bridge in the shortest path to the root-bridge, the designated bridge of the segment, and the port through which that segment accesses that bridge, the designated port. The spanning tree will include only the bridge ports that are either root-ports or designated-ports. For example, if we take as cost of a path the number of bridges it traverses, the following network is changed as indicated.

The Distributed Spanning Tree Algorithm is interesting as an example of the kind of algorithm that works in a distributed environment where no node has full knowledge of the network. Later in the course we will discuss more in detail the difficulties that arise in distributed environments.
In the Distributed Spanning Tree Algorithm bridges exchange messages using the standard set by IEEE 802.1. These messages, called configuration messages, use multicasting to a multicast group consisting of all and only the bridges on the same segment as the transmitting bridge. These messages are sent at network power-up to acquire information on the network topology, and then again whenever changes in topology are detected. Note that these configuration messages represent control traffic, that is overhead. A configuration message identifies, among other things:
Initially each bridge sends a configuration message on each
of its ports. This message has this bridge's id as root-bridge and as
transmitter and has 0 as cost. This message is saved at each port as
configuration for that port and as configuration for the bridge.
When a message is received at a port,
IF the received message is better than the current configuration
of the port THEN
it becomes the new configuration of this port;
IF it becomes the port with the best configuration THEN
it is said to be the root-port of the bridge and to be active.
[The root-port leads to the root-bridge and the first bridge
next on that path acts as the designated bridge of the current
bridge.]
The configuration of the root-port, with the transmitting bridge
field set to this bridge, and the cost incremented by one, if
better than the configuration of the bridge, becomes the new
configuration of the bridge. Then this new configuration is
compared to the configurations of all the non root ports. If the
configuration of a port is worse than the configuration
of that bridge, the port it is said to be active,
and the bridge configuration is transmitted through that port,
otherwise the port will become inactive.
[In reality if a port is to go from the inactive to the active
state, this transition will be delayed some time to make sure
that other ports that were supposed to go from active to
inactive have actually done so. This is required to avoid
transient loops between bridges.]
ELSE
this port becomes inactive;
END IF
The Spanning Tree consists of the bridges and their active ports
and the segments thus connected.


Each stored configuration message keeps an extra field representing the age of the message, i.e. the time since the root bridge sent the configuration message upon which this message is based. It is incremented each unit of time (timer-tick, usually 2 seconds) and when it reaches a preset maximum value maxAge (usually 20 seconds), the stored configuration for the port is reset to the initial value (current bridge as root bridge and source, cost and age set to 0). Then at this bridge is recomputed the best configuration (and root, cost to root, and root-port), thus another previously inactive port can become active. The root bridge sends at regular intervals Hello-time an heart-beat, an Hello-message to the bridges for which it is the designated bridge. When a bridge receives the Hello message it resets the age field for the receiving port to 0 and forwards its own configuration with age set to zero to the bridges for which it is the designated bridge. [maxAge should be larger than Hello-time plus the propagation time for the hello messages from the root to all the nodes in the spanning tree.]The effect of the hello message from the root bridge is to eliminate reconfiguration unless necessary.
Notice the interesting story we have seen about bridges:
Initialize arrays R and D so that for each vertex v of the graph, R[v] = NIL,
and D[v] is infinity except for s where D[s] = 0.
Finally let the set S consist of all the vertices of the graph.
Our intent is that for all vertices v, D[v] represents the current best
estimate of the cost of the paths from s to v and
R[v] is the next node (next-hop) in the current best path from
v to s.
While S is not empty
Let u be an element of S with minimal D value and remove it from S.
For each element v in the neighborhood of u that is in S
Let w = D[u] + cost-of-edge[u,v];
If D[v] is greater than w then //We are improving current path to v
Set D[v] to w;
Set R[v] to u;
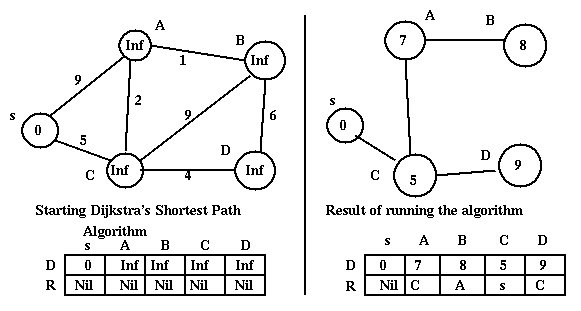
The Dijkstra shortest path algorithm is run independently at each vertex after the vertex has collected all the information on the structure of the graph. [There has to be a routing protocol (see below) to make this possible. The routing protocol associated with the Dijkstra shortest path algorithm (usually OSPF - Open Shortest Path First) allows each node to inform all other nodes of its own identity and of its links to its neighbors, its Link State.] Link state information is exchanged periodically (every few seconds), or when a new neighbor comes on line, or when it is recognised that a link is disabled. The message traffic generated is limited, as long as the number of nodes in the network does not become too great [if we have n nodes and each node has E neighbors, the information transmitted is proportional to n*E]. The Dijkstra shortest path algorithm computes the routing tables fairly quickly, but it tends to use substantial memory resources and to be not too stable (i.e. routes may change substantially as a consequence of changes in the cost associated to a few links)).
Note that Dijkstra's shortest path Algorithm creates a spanning tree with as root the node where the algorithm is run (s in the discussion above). The algorithm will result in different trees when run at different nodes - in fact each router node should run the algorithm). These spanning trees are not necessarily minimal (i.e. the sum of the cost of the branches is not minimal). For example:
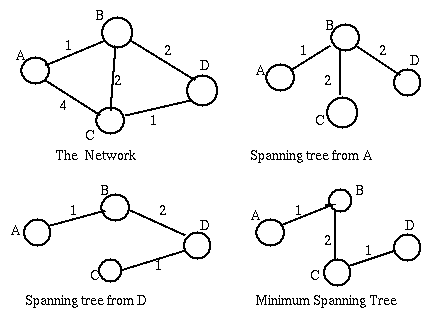
However the tree built by the Dijkstra shortest path algorithm at s will give the paths of minimal length from s to each of the other nodes.
Now each vertex s only knows itself and the distance to the neighbors
(we assume it to be 1 for simplicity).
Each vertex keeps a set of triples of the form
[destination, next-hop, distance]. This set is the distance vector.
Initially this set is {[s,NIL,0]} and it is transmitted to each neighbor.
When a vertex u receives a distance vector from its neighbor v
For each triple [d,n,c] in the received distance vector
Let w = c + distance from u to neighbor v (assumed to be 1);
[d,v,w] represents the new found path from u to d with
next step v;
If there is no triple of the form [d,x,y] in the distance
vector of u or
there is such a triple and (y > w or x=v) then
Remove [d,x,y], if there, and add [d,v,w] to the distance
vector of u. [Note that if x=v, we replace the old triple [d,x,y]
with the new triple [d,v,w] even if y<=w. This is so because it
is assumed that v has a more recent estimate of the path to d.]
When a vertex u recognizes that the link to a neighbor v has failed, it
Requests distance vector information from its remaining neighbors and
Recalculate the distance vector using the new neighborhood information.
A vertex sends a copy of its distance vector to its neighbors
whenever there has been a change in its own distance vector
or a failure in its neighborhood
Here is what the Vector Distance Algorithm
does in the case of the graph above:
Step 0:
s {[s,nil,0]}
A {[A,nil,0]}
B {[B,nil,0]}
C {[C,nil,0]}
D {[D,nil,0]}
Step 1:
s {[s,nil,0],[A,A,9],[C,C,5]}
A {[A,nil,0],[s,s,9],[B,B,1],[C,C,2]}
B {[B,nil,0],[A,A,1],[C,C,9[,[D,D,6]}
C {[C,nil,0],[s,s,5],[A,A,2],[B,B,9],[D,D,4]}
D {[D,nil,0],[C,C,4],[B,B,6]}
Step 2:
s {[s,nil,0],[A,C,7],[B,A,10],[C,C,5],[D,C,9]}
A {[A,nil,0],[s,C,7],[B,B,1],[C,C,2],[D,C,6]}
B {[B,nil,0],[s,A,10],[A,A,1],[C,A,3],[D,D,6]}
C {[C,nil,0],[s,s,5],[A,A,2],[B,A,3],[D,D,4]}
D {[D,nil,0],[s,C,9],[A,C,6],[C,C,4],[B,B,6]}
Step 3:
s {[s,nil,0],[A,C,7],[B,C,8],[C,C,5],[D,C,9]}
A {[A,nil,0],[s,C,7],[B,B,1],[C,C,2],[D,C,6]}
B {[B,nil,0],[s,A,8],[A,A,1],[C,A,3],[D,D,6]}
C {[C,nil,0],[s,s,5],[A,A,2],[B,A,3],[D,D,4]}
D {[D,nil,0],[s,C,9],[A,C,6],[C,C,4],[B,B,6]}
Notice that in the example we have glibly talked of "step 1", "step 2", etc. In reality distance vectors are transmitted asynchronously without any requirement that all nodes proceed in lockstep. Also, in reality the algorithm is more complex with nodes keeping separately the distance vectors of each neighbor, so that each node needs to transmit only changes in its distance vector, not each time the whole distance vector. Thus communication traffic is reduced.
A problem with the distance vector algorithm is its slowness in propagating the recognition of link failures (it is called the count-to-infinity problem). For example in the following graph
+---+ +---+ +---+
| A |----------| B |-----------| C |
+---+ +---+ +---+
suppose that we have the following distance vectors:
At A: {[A,NIL,0], [B,B,1], [C,B,2]}
At B: {[A,A,1], [B,NIL,0], [C,C,1]}
At C: {[A,B,2], [B,B,1], [C,NIL,0]}
and the link from B to C fails. So B discards the triple
[C,C,1] and recomputes the vector using the information from
A, thus it adds the triple [C,A,3]. This change in turn
is propagated to A that has to change its C triple to
[C,B,4], that causes B to change to [C,A,5], .. and so on
until "infinity" is reached and A and B can finally conclude that
C is unreacheable! An heuristic used is called split-horizon:
A would send to B the triple [C,B,+infinity] instead of [C,B,2]
(the +infinity sent to B reflects the fact that B was
the source of the actual value) . This triple will
be ignored by B as long as B is connected directly to C. But when
C becomes inaccessible that +infinity informs B that the
current information from A is un-usable.
[This heuristic does not solve more complex
cases of count-to-infinity problems.]