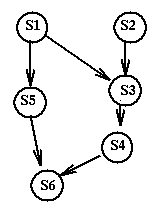
 If we have two processors P1 and P2 the algorithm would result in the schedule
If we have two processors P1 and P2 the algorithm would result in the schedule
P: abc
Q: def
a, b, c, d, e, f, are atomic actions. Each action has always the same
effect independent of what other actions may be executing at the same
time.
What is the effect of executing the two activities concurrently? We do
not know for sure, but we know that it will be the same as obtained by
executing sequentially an INTERLEAVING of the two activities. Here are
the possible interleavings of these two activities:
abcdef
abdcef
abdecf
abdefc
adbcef
......
defabc
That is, the actions of the two activities are sequenced in all
possible ways that preserve the order in which the actions appeared in
the two activities.
The inportance of the concept of interleaving is that it allows us to express the meaning of concurrent programs: The parallel execution of activities is equivalent to the sequential execution of one of the interleavings of these activities.
Since concurrent activities can have many interleavings, these interleavings may complete with different results. We will say that a set of activities (i.e. a program) is DETERMINATE if any time it runs, for the same inputs, it gives the same outputs. Otherwise it is NON-DETERMINATE (it has a RACE CONDITION).
Here are two activities that are not determinate. The first activity just executes the assignment a := 1; The second activity just executes the assignment a := 2;
Supposed that you are given the following two activities P and Q:
P: x := 2; Q: x := 3;
y := x - 1; y := x + 1;
What are the possible results of the parallel execution of these two
activities? [Answer: x=3 and y=4, or x=2 and y=1, or x=2 and y=3, or
x=3 and y=2. If you do not want to get some of these results, then you
have to prevent the occurrence of the interleavings that caused those
results. This is done with SYNCHRONIZATION MECHANISMS.]
Here is an example of undesirable interleaving (it has a name: the lost update phenomenon). Consider the following two sequences of actions performed by different processes (we assume that initially Account 1 has 1000 dollars - the actions represent two deposits to this account):
A1: Read value of Account 1 B1: Read value of Account 1
A2: Add 100 Dollars to it B2: Add 1000 Dollars to it
A3: Store value in Account 1 B3: Store value in Account 1
The interleaving A1 A2 B1 B2 B3 A3 will result in a balance of 1100 dollars and not 2100
dollars.
Here is another example of undesirable interleaving (it also has a name: the inconsistent retrieval phenomenon). Consider the following two sequences of actions performed by two different processes (we assume that initially Account 1 has 1000 dollars and Account 2 has 2000 dollars - The first sequence of actions represents the transfer of 100 dollars from Account 1 to Account 2; The second sequence of actions represents a report on the balances of these accounts):
A1: Read value of Account 1 B1: Read value of Account 1
A2: Subtract 100 dollars from it B2: Print this value
A3: Store value in Account 1 B3: Read value of Account 2
A4: Read value of Account 2 B4: Print this value
A5: Add 100 dollars to it
A6: Store value in Account 2
The interleaving A1 A2 A3 B1 B2 B3 B4 A4 A5 A6
will result in the apparent disappearence of 100 dollars.
In general problems arise between two concurrent applications
when there is a variable x that they both write to or to which
one writes and from which the other reads. In these cases the order
in which these operations are executed is significant. For example,
if there are concurrent writes to x, then the final value of x is the one
given by the last write. If an activity reads from x and another writes to x,
then the value read is the old or the new value of x depending on the
order in which these operations were executed.
The BERNSTEIN CONDITIONS express these observations
and are used to determine if a program is determinate.
The READ SET and the WRITE SET of an action A are respectively the set
of variables read by A and written by A. The Read Set of an activity
P, R(P), is the union of the read sets of all the actions of P.
Similarly, the Write Set of P, W(P), is the union of the write sets of
all the actions of P.
For example, if P is:
x := u + v;
y := x * w;
then R(P) = {u,v,x,w}, W(P) = {x, y}. Notice that x is both in R(P)
and in W(P).
Now the Bernstein Conditions:
Given activities P and Q, if
If these conditions are not satisfied, then it is still possible that the parallel execution of P and Q is determinate [can you come up with an example?], but usually it is not. [Note: We have discussed these conditions considering only two activities, but as you have guessed they generalize to more activities.]
The Bernstein Conditions are informative but too demanding: in most situations we want to execute activities that read/write the same data, and yet we don't want to give up determinacy. Thus something else is needed, some way of limiting the interleavings that are possible when executing activities in parallel. That is what SYNCHRONIZATION MECHANISMS do for us.
A node in a precedence graph could be a software task, as recognised by the operating system, or could be statements within a program that can be executed concurrently with respect to each other [see example below], or could describe some activity taking place during the execution of a single machine instruction. People refer to the different "sizes" of these concurrent activities, as the CONCURRENCY GRAIN of the representation. It goes from COARSE (the concurrency of operating systems task), to fine (the concurrency of single instructions, or of groups of instructions, as done for example in superscalar processors), to very fine (concurrency in the hardware during the execution of the single instruction).
EXAMPLE 1: Suppose we are given the following sequential program:
a := x + y; /* Statement s1 */
b := z + 1; /* Statement s2 */
c := a - b; /* Statement s3 */
w := c + 1; /* Statement s4 */
d := a + e; /* Statement s5 */
w := w * d; /* Statement s6 */
We can use the Bernstein conditions to derive a precedence graph from
this sequential program. The nodes in this graph are the statements
s1, s2, s3, s4, s5, s6.
 This precedence graph could be
executed using two processors. One processor could execute in order
s1, s5, s6 and the other s2, s3, s4. Of course they should synchronize
so that s3 executes after s1 and s6 after s4.This precedence graph is
MAXIMALLY PARALLEL for the given program. That is, the only
dependencies that appear in the graph are those required by the logic
of the program.
This precedence graph could be
executed using two processors. One processor could execute in order
s1, s5, s6 and the other s2, s3, s4. Of course they should synchronize
so that s3 executes after s1 and s6 after s4.This precedence graph is
MAXIMALLY PARALLEL for the given program. That is, the only
dependencies that appear in the graph are those required by the logic
of the program.
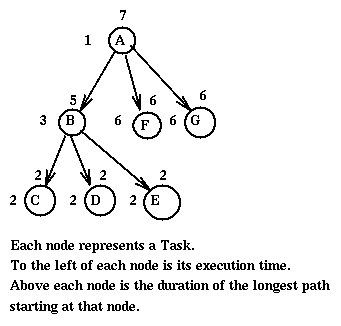
Given a precedence graph, how many processors should be used to execute it?
In general, given a precedence graph and given m processors, it becomes important to determine which tasks should be executed on each processor and in which order. If we only are interested in the question of which task is allocated to which processor [usually so that the processors are fairly equally loaded], we talk of Load Balancing. If we are interested in exactly which task runs where and in which order [usually so that the completion of all the tasks happens as early as possible], we talk of Scheduling.
There is a fairly simple way of scheduling (called list scheduling)
a precedence graph assuming that
all processors are alike. We assign "priorities" to the nodes (i.e. tasks).
Then when a processor becomes free,
we allocate to it the task with highest priority
among the unallocated tasks
all of whose predecessors have already terminated.
We often use as "priority" of a task
its optimal completion time [for each path starting
at this node we compute its execution time as the sum of the times
of the tasks on the path; we then take the maximum of these values for all
the paths starting at this node. Note that this is the
time of the critical path starting at this node.]. Note that this algorithm,
though often good, it does not guaranty optimality. For example in the
following precedence graph.
 If we have two processors P1 and P2 the algorithm would result in the schedule
If we have two processors P1 and P2 the algorithm would result in the schedule
On P1: A at time 0, F at time 1, B at time 7, C at time 10, E at time 12 On P2: G at time 1, D at time 10,with the last completion at time 14. We can do better with the schedule
On P1: A at time 0, F at time 1, C at time 7, D at time 9 On P2: B at time 1, G at time 4, E at time 10with the last completion at time 12.
Notice that the precedence graphs are acyclic, that is, they do not have loops. Thus they cannot represent cyclic computations. Since many of the computations in operating systems are cyclical [for example: wait for some event, respond to it, and then go back to waiting], this is a strong restriction. There are two ways out. One, represent each iteration as an acyclic graph; you will lose possible concurrency across two successive iterations, but you will be able to deal fully with concurrency within a single iteration. Two, give up on precedence graphs and use instead Petri Nets (Petri Nets are beyond the scope of our course).
ingargiola.cis.temple.edu